11: Spectrograms
- Page ID
- 96277
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Spectrograms visually represent the speach signal, and the calculation of the Spectrogram is briefly explained.
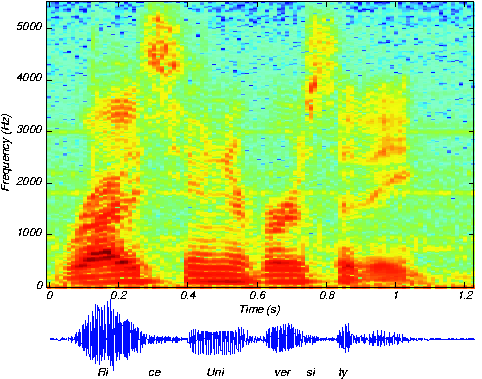
We know how to acquire analog signals for digital processing (pre-filtering, sampling, and A/D conversion) and to compute spectra of discrete-time signals (using the FFT algorithm), let's put these various components together to learn how the spectrogram shown Figure \(\PageIndex{1}\) below, which is used to analyze speech, is calculated. The speech was sampled at a rate of 11.025 kHz and passed through a 16-bit A/D converter.
Music compact discs (CDs) encode their signals at a sampling rate of 44.1 kHz. We'll learn the rationale for this number later. The 11.025 kHz sampling rate for the speech is 1/4 of the CD sampling rate, and was the lowest available sampling rate commensurate with speech signal bandwidths available on my computer.
Looking at Figure \(\PageIndex{1}\), the signal lasted a little over 1.2 seconds. How long was the sampled signal (in terms of samples)? What was the datarate during the sampling process in bps (bits per second)? Assuming the computer storage is organized in terms of bytes (8-bit quantities), how many bytes of computer memory does the speech consume?
Solution
Number of samples equals 1.2 × 11025 = 13230
The datarate is 11025 × 16 = 176.4 kbps
The storage required would be 26460 bytes
The resulting discrete-time signal, shown in the bottom of Figure \(\PageIndex{1}\) clearly changes its character with time. To display these spectral changes, the long signal was sectioned into frames: comparatively short, contiguous groups of samples. Conceptually, a Fourier transform of each frame is calculated using the FFT. Each frame is not so long that significant signal variations are retained within a frame, but not so short that we lose the signal's spectral character. Roughly speaking, the speech signal's spectrum is evaluated over successive time segments and stacked side by side so that the x-axis corresponds to time and the y-axis frequency, with color indicating the spectral amplitude.
An important detail emerges when we examine each framed signal from the above figure.
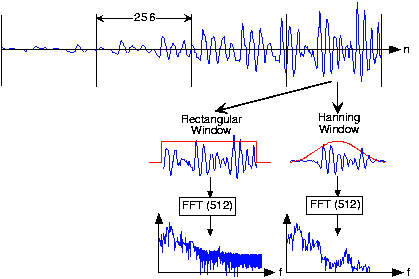
At the frame's edges, the signal may change very abruptly, a feature not present in the original signal. A transform of such a segment reveals a curious oscillation in the spectrum, an artifact directly related to this sharp amplitude change. A better way to frame signals for spectrograms is to apply a window: Shape the signal values within a frame so that the signal decays gracefully as it nears the edges. This shaping is accomplished by multiplying the framed signal by the sequence w(n). In sectioning the signal, we essentially applied a rectangular window:
\[w(n)=1,0\leq n\leq N-1 \nonumber \]
A much more graceful window is the Hanning window; it has the cosine shape
\[w(n)=\frac{1}{2}\left ( 1-\cos \left ( \frac{2\pi n}{N}\right )\right ) \nonumber \]
As shown in Figure \(\PageIndex{2}\), this shaping greatly reduces spurious oscillations in each frame's spectrum. Considering the spectrum of the Hanning windowed frame, we find that the oscillations resulting from applying the rectangular window obscured a formant (the one located at a little more than half the Nyquist frequency).
What might be the source of these oscillations? To gain some insight, what is the length-2N discrete Fourier transform of a length-N pulse? The pulse emulates the rectangular window, and certainly has edges. Compare your answer with the length-2N transform of a length-N Hanning window.
Solution
The oscillations are due to the boxcar window's Fourier transform, which equals the sinc function.
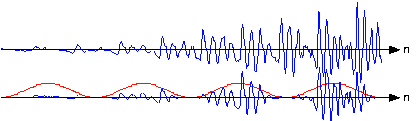
If you examine the windowed signal sections in sequence to examine windowing's effect on signal amplitude, we see that we have managed to amplitude-modulate the signal with the periodically repeated window (Figure \(\PageIndex{3}\)). To alleviate this problem, frames are overlapped (typically by half a frame duration). This solution requires more Fourier transform calculations than needed by rectangular windowing, but the spectra are much better behaved and spectral changes are much better captured.
The speech signal, such as shown in the Figure \(\PageIndex{1}\) above, is sectioned into overlapping, equal-length frames, with a Hanning window applied to each frame. The spectra of each of these is calculated, and displayed in spectrograms with frequency extending vertically, window time location running horizontally, and spectral magnitude color-coded. Figure 5.10.4 illustrates these computations.
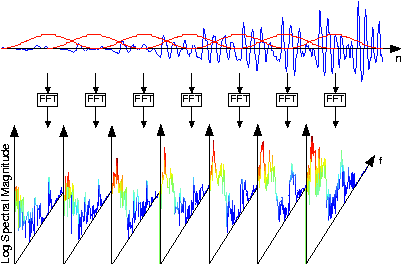
Why the specific values of 256 for N and 512 for K? Another issue is how was the length-512 transform of each length-256 windowed frame computed?
Solution
These numbers are powers-of-two, and the FFT algorithm can be exploited with these lengths. To compute a longer transform than the input signal's duration, we simply zero-pad the signal.


