8.3: Chelation

A metal ion in solution does not exist in isolation, but in combination with ligands (such as solvent molecules or simple ions) or chelating groups, giving rise to complex ions or coordination compounds. These complexes contain a central atom or ion, often a transition metal, and a cluster of ions or neutral molecules surrounding it.

Introduction

Many complexes are relatively unreactive species remaining unchanged throughout a sequence of chemical or physical operations and can often be isolated as stable solids or liquid compounds. Other complexes have a much more transient existence and may exist only in solution or be highly reactive and easily converted to other species. All metals form complexes, although the extent of formation and nature of these depend very largely on the electronic structure of the metal. The concept of a metal complex originated in the work of Alfred Werner, who in 1913 was awarded the first Nobel Prize in Inorganic chemistry.

Complexes may be non-ionic (neutral) or cationic or anionic, depending on the charges carried by the central metal ion and the coordinated groups. The total number of points of attachment to the central element is termed the coordination number and this can vary from 2 to greater than 12, but is usually 6. The term ligand come from the latin word ligare, which meaning to bind) was first used by Alfred Stock in 1916 in relation to silicon chemistry. The first use of the term in a British journal was by H. Irving and R.J.P. Williams in Nature, 1948, 162, 746 in their paper describing what is now called the Irving-Williams series.

Ligands can be further characterised as monodentate, bidentate, tridentate etc. where the concept of teeth (dent) is introduced, hence the idea of bite angle etc. The term chelate was first applied in 1920 by Sir Gilbert T. Morgan and H.D.K. Drew [J. Chem. Soc., 1920, 117, 1456], who stated: "The adjective chelate, derived from the great claw or chela (chely- Greek) of the lobster or other crustaceans, is suggested for the caliperlike groups which function as two associating units and fasten to the central atom so as to produce heterocyclic rings."

Metal complexation is of widespread interest. It is studied not only by inorganic chemists, but by physical and organic chemists, biochemists, pharmacologists, molecular biologists and environmentalists.

Thermodynamic Stability

The "stability of a complex in solution" refers to the degree of association between the two species involved in the state of equilibrium. Qualitatively, the greater the association, the greater the stability of the compound. The magnitude of the (stability or formation) equilibrium constant for the association, quantitatively expresses the stability. Thus, if we have a reaction of the type:

\[M + 4L \rightarrow ML_4\]

then the larger the stability constant, the higher the proportion of \(ML_4\) that exists in the solution. Free metal ions rarely exist in solution so that \(M\), will usually be surrounded by solvent molecules which will compete with the ligand molecules, \(L\), and be successively replaced by them. For example in water:

\[ M(H_2O)_4 + L \rightleftharpoons M(H_2O)_3L + H_2O\]

\[ M(H_2O)_3L + L \rightleftharpoons M(H_2O)_2L_2 + H_2O\]

However, for simplicity, we generally ignore these solvent molecules and write four stability constants as follows:

\(M + L → ML\) with \[K_1 = \dfrac{[ML]}{[M] [L]}\]

\(ML + L → ML_2\) with \[K_2 = \dfrac{[ML_2]}{[ML] [L]}\]

\(ML_2 + L → ML_3\) with \[K_3 = \dfrac{[ML3]}{[ML_2] [L]}\]

\(ML_3 + L → ML_4\) with \[K_4 = \dfrac{[ML_4]}{[ML_3] [L]}\]

where \(K_1\), \(K_2\) etc. are referred to as "stepwise stability constants." Alternatively, the "Overall Stability Constant" can be constructed

\[ M + 4L \rightarrow ML_4 \beta_4 = \dfrac{[ML_4]}{[M] [L]^4}\]

The stepwise and overall stability constants are therefore related as follows:

\[\beta_4 =K_1 \times K_2 \times K_3 \times K_4 \]

or more generally,

\[ \beta_n =K_1 \times K_2 \times K_3 \times K_4 \times ... K_n\]

Table E4 outlines the sequential formation constants for a range of metal-ligand complexes.

Example \(\PageIndex{1}\): The Cuprammonium Ion

Consider the four steps involved in the formation of the cuprammonium ion \(Cu(NH_3)_4^{2+}\):

STEP 1:

\[Cu^{2+} + NH_3 \rightleftharpoons Cu(NH_3)^{2+}\]

with

\[K_1 = \dfrac{[Cu(NH_3)^{2+}]}{[Cu^{2+}] [NH_3]}\]

STEP 2:

\[ CuNH_3^{2+} + NH_3 \rightleftharpoons Cu(NH_3)_2^{2+}\]

with

\[K_2 = \dfrac{ [Cu(NH_3)_2^{2+}]}{[Cu(NH_3)^{2+}] [NH_3]}\]

STEP 3:

\[ Cu(NH_3)_2^{2+} + NH_3 \rightleftharpoons Cu(NH_3)_3^{2+}\]

with

\[K_3 = \dfrac{ [Cu(NH_3)_3^{2+}]}{[Cu(NH_3)_2^{2+}] [NH_3]}\]

STEP 4:

\[ Cu(NH_3)_3^{2+} + NH_3 \rightleftharpoons Cu(NH_3)_4^{2+}\]

with

\[K_4 = \dfrac{ [Cu(NH_3)_4^{2+}]}{[Cu(NH_3)_3^{2+}] [NH_3]}\]

where the \(\{K\}\) constants are the stepwise stability constants. Also:

\[\beta_4 = \dfrac{[Cu(NH_3)_4^{2+}]}{[Cu^{2+}] [NH_3]^4}\]

The addition of the four ammine groups to copper shows a pattern found for most formation constants, in that the successive stability constants decrease. In this case, the four constants are:

\[\log K_1 =4.0,\]

\[\log K_2 =3.2,\]

\[\log K_3 =2.7,\]

\[\log K_4 =2.0 \; \text{or} \; \log \beta_4 =11.9\]

Pay attention to definitions: a number of texts may refer to \(\beta_4\) as the instability constant or the dissociation constant of coordination complexes (e.g., termed \(\beta'_4\) below) , which corresponds to the reciprocal of the formation constant (\(K_4\)), since the reactions referred to are those where fully formed complexes break down to the aqua ion and free ligands. For example,

\[\beta'_4 = \dfrac{[Cu^{2+}] [NH_3]^4}{[Cu(NH_3)_4^{2+}]}\]

However, this is not definition use here (Table E4) and should be compared with the equation for the formation constant given earlier.

It is usual to represent the metal-binding process by a series of stepwise equilibria which lead to stability constants that may vary numerically from hundreds to enormous values such as 10³⁵ and more. That is

100,000,000,000,000,000,000,000,000,000,000,000.0

For this reason, they are commonly reported as logarithms. So log₁₀ (β) = log₁₀ (10³⁵) = 35. It is additionally useful to use logarithms, since log(K) is directly proportional to the free energy of the reaction.

\[ΔG^o = -RT \ln(β)\]

\[ΔG^o = -2.303 RT \log_{10}(β)\]

\[ΔG^o = ΔH^o - TΔS^o\]

Below are three tables of the formation constants and thermodynamics properties of example ligand-metal complexes; a more complete table can be found in Table E4.

Table \(\PageIndex{1}\): Reaction of ammonia and 1,2-diaminoethane with Cd²⁺.

# of ligands	ΔG° (kJmol^-1)	ΔH° (kJmol^-1)	ΔS° (JK-1mol^-1)	log β
2 NH3(1 en)	-28.24 (-33.30)	-29.79 (-29.41)	-5.19 (+13.05)	4.95 (5.84)
4 NH3(2 en)	-42.51 (-60.67)	-53.14 (-56.48)	-35.50 (+13.75)	7.44 (10.62)

Table \(\PageIndex{2}\): Reaction of pyridine and 2,2'-bipyridine with Ni²⁺.

# of ligands	log β	ΔG° (kJmol^-1)
2 py (1 bipy)	3.5 (6.9)	-20 (-39)
4 py (2 bipy)	5.6 (13.6)	-32 (-78)
6 py (3 bipy)	9.8 (19.3)	-56 (-110)

Table \(\PageIndex{3}\): Reaction of ammonia and 1,2-diaminoethane with Ni²⁺.

# of ligands	log β	ΔG° (kJmol^-1)
1 NH3	2.8	-16
2 NH3 (1 en)	5.0 (7.51)	-28.5 (-42.8)
3 NH3	6.6	-37.7
4 NH3 (2 en)	7.87 (13.86)	-44.9 (-79.1)
5 NH3	8.6	-49.1
6 NH3 (3 en)	8.61 (18.28)	-49.2 (-104.4)

The Chelate Effect

The chelate effect can be seen by comparing the reaction of a chelating ligand and a metal ion with the corresponding reaction involving comparable monodentate ligands. For example, comparison of the binding of 2,2'-bipyridine with pyridine or 1,2-diaminoethane (ethylenediamine=en) with ammonia. It has been known for many years that a comparison of this type always shows that the complex resulting from coordination with the chelating ligand is much more thermodynamically stable. This can be seen by looking at the values for adding two monodentates compared with adding one bidentate, or adding four monodentates compared to two bidentates, or adding six monodentates compared to three bidentates.

A number of points should be highlighted from the formation constants in Table E4. In Table \(\PageIndex{1}\), it can be seen that the ΔH° values for the formation steps are almost identical, that is, heat is evolved to about the same extent whether forming a complex involving monodentate ligands or bidentate ligands. What is seen to vary significantly is the ΔS° term which changes from negative (unfavorable) to positive (favorable). Note as well that there is a dramatic increase in the size of the ΔS° term for adding two compared to adding four monodentate ligands. (-5 to -35 JK^-1mol^-1). What does this imply, if we consider ΔS° to give a measure of disorder?

In the case of complex formation of Ni²⁺ with ammonia or 1,2-diaminoethane, by rewriting the equilibria, the following equations are produced.

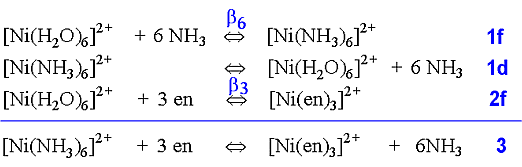
Using the equilibrium constant for the reaction (3 above) where the three bidentate ligands replace the six monodentateligands, we find that at a temperature of 25° C:

\[\Delta G^° = -2.303 \, RT \, \log_{10} K\]

\[= -2.303 \,RT \,(18.28 - 8.61)\]

\[= -54 \text{ kJ mol}^{-1}\]

Based on measurements made over a range of temperatures, it is possible to break down the \(\Delta G^°\) term into the enthalpy and entropy components.

\[\Delta G^° = \Delta H^° - T \Delta S^°\]

The result is that: \(\Delta H^° = -29 kJ mol^{-1}\)

- TΔS° = -25 kJ mol^-1
and at 25C (298K)
ΔS° = +88 J K^-1 mol^-1

For many years, these numbers have been incorrectly recorded in textbooks. For example, the third edition of "Basic Inorganic Chemistry" by F.A. Cotton, G. Wilkinson and P.L. Gaus, John Wiley & Sons, Inc, 1995, on page 186 gives the values as:

ΔG° = -67 kJ mol^-1
ΔH° = -12 kJ mol^-1
-TΔS° = -55 kJ mol^-1

The conclusion they drew from these incorrect numbers was that the chelate effect was essentially an entropy effect, since the TΔS° contribution was nearly 5 times bigger than ΔH°.

In fact, the breakdown of the ΔG° into ΔH° and TΔS° shows that the two terms are nearly equal (-29 and -25 kJ mol^-1, respectively) with the ΔH° term a little bigger! The entropy term found is still much larger than for reactions involving a non-chelating ligand substitution at a metal ion. How can we explain this enhanced contribution from entropy? One explanation is to count the number of species on the left and right hand side of the equation above.

It will be seen that on the left-hand-side there are 4 species, whereas on the right-hand-side there are 7 species, that is a net gain of 3 species occurs as the reaction proceeds. This can account for the increase in entropy since it represents an increase in the disorder of the system. An alternative view comes from trying to understand how the reactions might proceed. To form a complex with 6 monodentates requires 6 separate favorable collisions between the metal ion and the ligand molecules. To form the tris-bidentate metal complex requires an initial collision for the first ligand to attach by one arm but remember that the other arm is always going to be nearby and only requires a rotation of the other end to enable the ligand to form the chelate ring.

If you consider dissociation steps, then when a monodentate group is displaced, it is lost into the bulk of the solution. On the other hand, if one end of a bidentate group is displaced the other arm is still attached and it is only a matter of the arm rotating around and it can be reattached again. Both conditions favor the formation of the complex with bidentate groups rather than monodentate groups.

References

1. For a fascinating review of the origin and dissemination of the term 'ligand' in chemistry see: W.H. Brock, K.A Jensen, C.K. Jorgensen and G.B. Kauffman, Polyhedron, 2, 1983, 1-7.
2. Gilbert T. Morgan and H.D.K. Drew, J. Chem. Soc., 1920, 117, 1456
3. H. Irving and R.J.P. Williams, Nature, 1948, 162, 746
4. A description of his Alfred Werner's life and the influence his work played in the development of coordination chemistry is given by G.B. Kauffman in "Inorganic Coordination Compounds", Heyden & Son Ltd, 1981.

Problems

Calculate the entropy changes at 25°C, for the following reactions:

Zn²⁺ + 2NH₃ <=> [Zn(NH₃)₂]²⁺

ΔH = -28.03 kJ mol^-1 and log₁₀ β₂ = 5.01

Zn²⁺ + en <=> [Zn(en)]²⁺

ΔH = -27.6 kJ mol^-1 and log₁₀ β = 6.15 (NB R=8.314 JK^-1mol^-1)

Solution

The calculations make use of the equations:

ΔG° = RTlnβ
ΔG° = 2.303RTlog₁₀β
ΔG° = ΔH° - TΔS°

First it is necessary to calculate the ΔG values from the given formation constants and temperature 25C = 298K.

For the ammonia complex, ΔG = -8.314 * 298 * 2.303 * 5.01 kJmol^-1, that is -28.6 kJmol^-1.

For the 1,2-diaminoethane complex, ΔG= -8.314 * 298 * 2.303 * 6.15 kJmol^-1 which corresponds to -35.1 kJmol^-1.

This makes use of the relation between Ln and log10 such that ln(x) = 2.303 log10 (x).

Then using the second relationship above, ΔS can be found.

\[\Delta S = \dfrac{\Delta H - \Delta G}{T}\]

For the ammonia complex this gives 1.9 JK^-1mol^-1 and for the 1,2-diaminoethane complex 25.2 JK^-1mol^-1, which are the values given as answer 2.

Contributors and Attributions

• Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)