In order to understand electrical circuit behavior we must first define what it is that we are chasing. Ultimately, electrical circuits are all about the movement of electric charge. What do we mean by charge? To answer that question, we need to come up with a usable model of an atom, in other words, a functional description of its internal structure. To be sure, atoms are far smaller than most people imagine. There are far more atoms in a gallon of water than there are gallons of water in all of the oceans, lakes and rivers of planet Earth combined. It would be pointless to ask what an atom might “look like” because its components are all smaller than the shortest wavelengths of light that humans can see. That would be a little like asking a human what a dog whistle sounds like, when in fact it's at a pitch that's higher than humans can hear. Ultimately though, all we really need is a model to explain its observed behavior.
Perhaps the most prolific model in the popular imagination is the planetary model shown in Figure 2.2.1
, so named because it is reminiscent of simple models of our solar system. In this model, the core, or nucleus, is drawn at the center and contains positively charged protons and non-charged neutrons. Revolving around this core are negatively charged electrons, each following a nice, regular, planar path much like a planet around the sun. Unfortunately, this model is not accurate to say the least, although its popularity can sometimes lead to wildly erroneous and darkly humorous conclusions. In spite of its inaccuracy, the components (nucleus, protons, neutrons and electrons) are perfectly valid. Before we come up with a more accurate and useful model, let's take a closer look at these items.
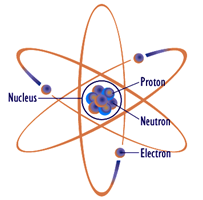
Figure 2.2.1
: Planetary atomic model: Popular but sadly incorrect. Image source (modified)
Unlike people, all particles of a type are indistinguishable: every proton is identical to every other proton and every electron is identical to every other electron. The number of protons determine what the element is. The simplest element, hydrogen, has a single proton in its nucleus. In contrast, helium has two protons in its nucleus and copper has 29. The nucleus may also contain a number of neutrons as well (not necessarily equal to the number of protons). In any stable atom, the number of electrons will equal the number of protons. If they aren't the same, the atom is called an ion (technically, a cation has fewer electrons than protons and an anion is its opposite). With an external energy source, it is possible to separate an electron from an atom. This leaves us with an electron and an atom that now has a net positive charge. It is this ability to separate these particles, and thus separating charge, that gives rise to our concept of electricity including such items as current and voltage, as we shall see.
Most of the mass of any given atom is from the protons and neutrons. Protons and neutrons have similar masses, about 1.67E−24 grams each. The mass of an electron is roughly 2000 times smaller. The radius of a proton is approximately 0.87E−15 meters and the mean distance to the nearest electron is about 5.3E−11 meters. Therefore an electron is about 60,000 times farther away from the proton than the size of said proton. To put this into perspective, that's roughly the same as the ratio between a golf ball and a sphere with a radius of 3/4ths of a mile or 1200 meters. This would be the case for a hydrogen atom as it consists of a single proton and electron. The magnitude of this ratio is not much different for other substances, including things like diamond and quartz that are very hard and solid. If you think about that for a moment, you realize that the idea of “solidity” is in some ways an illusion because the vast majority of what we call “something” is really just empty space (like a golf ball rattling around inside a sphere that's a mile and a half wide). In reality, the feeling of solidity when you grab something with your hand is just the result of the interaction of atomic forces between your hand and the object. Indeed, if we could somehow get rid of that “empty space”, we could fit a mountain inside of a car (although it would probably require a severely upgraded suspension).
For our immediate work, perhaps the most important issue is that of charge, an essential part of the theory of electromagnetism. It was mentioned that protons are positively charged and electrons are negatively charged. What then is charge? Charge is not an obvious physical attribute like someone's height or eye color. It's closer to a behavioral characteristic. Saying a particle is charged is like saying someone has an attractive personality. The magnitude of the charge on an electron is the same as the magnitude of the charge on a proton. The only difference is the polarity: protons are positively charged while electrons are negatively charged. An important thing to remember is that particles with the same polarity repel each other while opposites attract1.
Charge is measured in coulombs, named after Charles-Augustin de Coulomb a French physicist of the eighteenth century. The charge on a single electron is tiny, a mere 1.602E−19 coulombs. Alternately, it takes 6.242E18 electrons to create a charge of one coulomb. More on this in a moment.
One of the major issues with the planetary model is the idea that electrons whirl around the nucleus in stable, planet-like orbits. That's simply not true. First, the electron inhabits a region of 3D space and does not simply move through a plane. Second, due to the Heisenberg Uncertainty Principle, we can't precisely plot the position and trajectory of a given electron. The best we can do is make a plot of where the electron is likely to be. This is called a probability contour. To understand this concept, imagine that you could record the position of a specific electron relative to the nucleus at a specific time. A moment later you record its new position, a moment after that you record the next position, and so on for thousands of measurements. If you attempted to plot them all, you would wind up with a cloud of dots around the nucleus. This cloud is referred to as an orbital. You wouldn't know how the electron got from one position to the next but you would get a general idea of where it was likely to be. Ultimately, an orbital looks nothing like a planetary orbit.
A good analogy to an electron probability contour is the mapping of the flight of migratory birds. For example, a certain group of Canada geese might migrate from their summer range in the far north of Canada to their summer abode in the southern USA via s section of the Atlantic Flyway, perhaps through central New York State, as shown in purple, in Figure 2.2.2
. The flyway tells you where these birds are likely to be found while migrating. If they are taking the route through central New York, at some point it is likely that any particular goose in that flock will be found near the cities of Utica, Syracuse and so forth. It is much less likely that any particular goose from that flock will be found in Ohio or New Hampshire. Texas, of course, is right out. The flyway gives a good bit of data regarding where these birds are likely to be but in no way can it predict with any accuracy precisely where any individual bird will be on a specific date, nor precisely where it will end its migration.
Figure 2.2.2
: Electron behavior versus migratory birds.
Returning from our avian diversion, we note that there are several potential orbitals. Due to quantum physics, only certain orbitals are allowed. The permissible electron energy levels are first grouped into shells, then subshells and finally orbitals. It is important to remember that orbitals indicate the electron energy level. That is, a higher orbital implies a higher energy level. Further, orbitals fill in first from lowest energy level to highest energy level.
Shells are denoted by their principal quantum number, \(n\); 1, 2, 3, etc. The higher the number, the more subshells it can contain. Subshells are designated by letters, the first four being \(s\), \(p\), \(d\), and \(f\). Shell 1 contains only subshell \(s\) while shell 2 contains subshell types \(s\) and \(p\). Shell 3 contains subshell types \(s\), \(p\) and \(d\), and so on. These subshells may also have variations within them. There is one variation on \(s\), three variations on \(p\), five variations on \(d\), etc. These variations are the orbitals and each orbital can hold a maximum of two electrons.
Putting this all together, we find that the first shell can contain a maximum of two electrons: two in the single \(s\) subshell orbital (\(1s\)). The second shell can contain a maximum of eight electrons: two in the \(s\) subshell (\(2s\)) plus two in each of the three \(p\) subshell orbitals (\(2p\)). In like manner the third shell can contain a maximum of 18 electrons: two in \(3s\), six in \(3p\) and two in each of the the five \(d\) subshell orbitals (\(3d\)). You can condense this into a simple formula:
\[\text{Number of electrons per shell } = 2n^2, \text{ where } n \text{ is the shell number} \nonumber \]
Figure 2.2.3
shows the electron probability contour of the innermost orbital, namely \(1s\) (i.e., principle quantum number 1, subshell \(s\)). As you can see, it is spherical in shape. The nucleus is located at the center, obscured here. All \(s\) orbitals are similarly spherically shaped although the internals change. \(1s\) is the lowest energy orbital.

Figure 2.2.3
: Electron probability contour for innermost orbital, 1s.
Orbitals are not limited to simple spherical shapes. Higher order orbitals can take on a variety of forms. Figure 2.2.4
shows a much more complex electron probability contour. The nucleus is situated in the center of the concentric rings. Obviously, this is nothing like the well-behaved elliptical orbits of planets around the sun (nor the paths of migratory birds, unless they are very confused).

Figure 2.2.4
: A higher order electron probability contour.
As visually interesting as these graphics are, they are cumbersome to work with. Consequently, a more functional graphic is called for. Such a device is the Bohr model, named after Danish physicist Niels Bohr. An example is shown in Figure 2.2.5
.
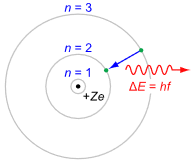
Figure 2.2.5
: Generic Bohr model.
It is important to understand that the Bohr model is an energy description of the atom, not an attempt to mimic its physical appearance or structure. The nucleus is placed at the center. It is surrounded by concentric rings that represent the electron shells. The higher the number, the larger the ring and the greater the energy level. If an electron were to move from a higher level to a lower level, the energy difference is radiated out. This could be in the form of heat or light. This is a point worth remembering. For example, this transition is what makes light emitting diodes (LEDs) function. The inverse is also possible, namely that by absorbing energy, an electron can move into a higher orbital. This is an equally powerful concept.
Using the Bohr model we can create diagrams to represent individual elements. For example, copper has an atomic number of 29 meaning that it has 29 protons and 29 electrons. The electron shell configuration is 2-8-18-1. That is, the first three shells are completely filled and there is a single electron in the fourth shell. The Bohr model for copper would simply show four rings, the first three being filled and with a single electron in the fourth ring. This is shown in Figure 2.2.6
. In this version, the individual electrons are drawn in each shell and the atomic number is indicated at the nucleus. Again, please do not imagine this representing individual electrons orbiting the nucleus in lanes. This is an energy level depiction.
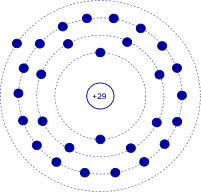
Figure 2.2.6
: Bohr model of copper.
It is worth noting that a lone outer electron is only loosely bound to the nucleus thus making the movement of charge through said material relatively easy, given the application of some external energy source. Consequently, copper is a very good conductor. This is a characteristic shared by common metals: they are good conductors because they only have one or two loosely held electrons in their outer shell. Examples include silver, gold and aluminum (one outer electron for each, all of them being very good conductors); and iron, tin and nickel (two outer electrons for each, and this group being not quite as conductive as those in the first group).
References
1The obvious question might be “Why doesn't the nucleus break apart?” The answer is that the sub-atomic strong nuclear force has a greater effect at atomic distances than electromagnetism, and thus binds the protons and neutrons together in the nucleus.








