Seeing the usefulness of negative feedback, it would be nice if we could apply the concept to our electronic circuits. The basic idea is quite simple, really. What we will do is sample a piece of the output signal, and then add it to the input signal out of phase (i.e., subtract it). By doing so, the circuit will see the difference between the input and the output. If the output signal is too large, the difference will be negative. Conversely, the difference signal will be positive if the output is too small. This signal is then multiplied by the circuit gain and cancels the output error. Thus, the circuit will be presented with the undesired errors in a way that will force the output to compensate (move in the opposite direction). This process is done continuously; the only time lags involved are the propagation delays of the circuits used.
Because the sampled output signal is effectively subtracted from the input signal, negative feedback is sometimes referred to as degenerative or destructive feedback. This subtraction can be achieved in a variety of ways. A differential amplifier is tailor made for this task because it has one inverting input and one noninverting input. (Note: If the error is presented in phase, the circuit magnifies the errors and positive feedback results.)
To see an example of how this works, refer to Figure \(\PageIndex{1}\). The triangle represents an amplifying circuit. It has a gain of \(A\). The output signal is also presented to the input of the feedback network represented by the box. This network scales the output signal by a factor, \(\beta\). The feedback network ranges from very simple to complex. It may contain several resistors, capacitors, diodes and what not, or it may be as simple as a single piece of wire. In any case, this scaled output signal is referred to as the feedback signal and is effectively subtracted from the input signal. This combination, called the error signal, is then fed to the amplifier where it is boosted and appears at the output. The process repeats like this forever (or at least until the power is switched off).
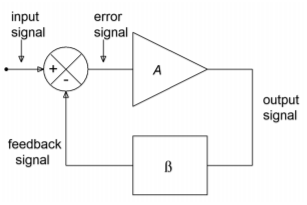
Figure \(\PageIndex{1}\): Negative feedback.
Let's assume that for some reason (perhaps a temperature change) the amplifier's gain were to rise. This should make the output signal increase by a similar percentage, but it doesn't. Here's why: As the output signal tries to rise, the feedback signal tracks with it. Now that there is a larger feedback signal, the error signal will become smaller (remember, error = input - feedback). This smaller signal is multiplied by the gain of the amplifier, thus producing a smaller output signal that almost completely offsets the original positive change. Note that if the output signal were too small, the error signal would increase, thus bringing the output back up to a normal level. When everything is working right, the feedback and input signals are almost the same size. (Actually, the feedback signal is somewhat smaller in magnitude.)
3.3.1: The Effects of Negative Feedback
Besides smoothing out gain anomalies, negative feedback can reduce the effect of device non-linearities, thus producing a reduction in static forms of distortion such as THD (Total Harmonic Distortion). Basically, these non-linearities can be viewed as a string of small gain errors. As such, they produce appropriate error signals and are compensated for in the above manner. Negative feedback can also increase the bandwidth of the system. It can increase the upper cutoff frequency \(f_2\) and decrease the lower cutoff frequency \(f_1\) (assuming the system has one). Also, we can exercise control over the input and output impedances of the circuit. It is possible to increase or decrease the impedances. As you might have guessed, we don't receive these benefits for nothing. The down side to negative feedback is that you lose gain. Effectively, you get to trade off gain for an increase in bandwidth, a decrease in distortion, and control over impedances. The more gain you trade off, the greater your rewards in the other three areas. In the case of our op amp, this is a wise tradeoff because we already have more gain than we need for typical applications. This give-and-take is a very important idea, so remember “BIG D”. That stands for Bandwidth, Impedance, Gain, and Distortion
At this point, we need to define a few terms. Closed loop refers to the characteristics of the system when feedback exists. For example, closed-loop gain is the gain of the system with feedback, whereas closed-loop frequency response} refers to the new system break points. Generalized closed-loop quantities will be shown with the subscript "\(cl\)". Similarly, we will denote impedances, gain and the like for specific feedback variants with a two- letter subscript abbreviating the exact feedback configuration. One possibility for closed-loop gain would be \(A_{sp}\). Open loop refers to the characteristics of the amplifier itself. To remember this, think of disconnecting or opening the path through the feedback network. Once the path is broken, the amplifier is on its own. Open-loop gain then, refers to the gain of the amplifier by itself, with no feedback. All open-loop quantities will be shown with the subscript "\(ol\)". The symbol for open-loop gain would be \(A_{ol}\). The term loop gain refers to the ratio between the open- and closed-loop gains (it may also be computed from their difference in decibels on a Bode plot). Loop gain indicates how much gain we have given up or sacrificed in order to enhance the operation of the system. Consequently, loop gain is often called sacrifice factor, and given the symbol \(S\). Generally, tradeoffs are proportional to the sacrifice factor. For example, if we cut the gain in half, we will generally double the bandwidth, and halve the distortion. An example that illustrates this can be seen in Figure \(\PageIndex{2}\). Note how the loop gain decreases with increasing frequency. This means that the effects of feedback at higher frequencies are not as great.
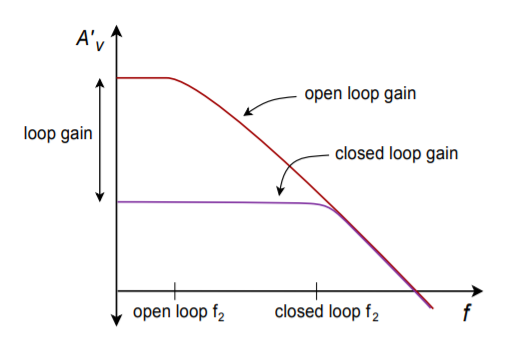
Figure \(\PageIndex{2}\): Response with and without feedback.
Up to this point we have made one simple assumption about our system; that it exhibits no “extra” phase change beyond the desired inversion. As we saw in the first chapter, however, all circuits do produce phase changes as the input frequency is increased. If this extra phase change were to reach -180\(^{\circ}\) while the gain was greater than unity (0dB), our negative feedback will turn into positive feedback (the inversion = -180\(^{\circ}\), plus this extra -180\(^{\circ}\), places us at -360\(^{\circ}\). The net result is an inphase signal). If this were to happen, our amplifier would no longer be stable. In fact, it may very well turn into a high frequency oscillator. (You will see how to do this on purpose when you cover Chapter Nine). As the input frequency is raised, the phase will eventually exceed -180\(^{\circ}\) and the gain will drop to a fraction (< 0dB). The real key here is making sure that the phase never reaches or exceeds -180\(^{\circ}\) when the gain falls to 1. Stated another way, when the phase hits -180\(^{\circ}\), the gain should be a fraction. Generally, the farther you are from this “danger zone”, the better. In other words, you're better off if the extra phase at the unity gain point is -90\(^{\circ}\) rather than -170\(^{\circ}\). Both are stable, but the first one gives you some breathing room.
Two measures of circuit safety are the gain and phase margins. Phase margin indicates the difference between the actual phase at unity gain and -180\(^{\circ}\). In the example above the first circuit would have a phase margin of 90\(^{\circ}\) and the second would have a margin of 10\(^{\circ}\). Gain margin is the difference between the actual gain in dB at the -180\(^{\circ}\) phase point, and 0dB. If our gain was -9 dB at -180\(^{\circ}\), the gain margin would be 9 dB (i.e., we have 9 dB “to spare”). Reasonable values for gain and phase margin are > 6 dB and > 45\(^{\circ}\). Gain and phase margins are depicted in Figure \(\PageIndex{3}\). It is possible to guarantee safe margins if the amplifier's open loop response maintains a 20 dB-per-decade rolloff up to the unity gain frequency, \(f_{unity}\). This means that there is only one dominating lag network that will add a maximum phase shift of -90\(^{\circ}\). Even if the second network coincided with \(f_{unity}\), it would add -45\(^{\circ}\) at most. This would still leave us with a 45\(^{\circ}\) phase margin. (Note that if we had several secondary networks critical at \(f_{unity}\) the phase could exceed -180\(^{\circ}\), however the slope would no longer be 20 dB-per-decade in reality.) It is for this reason that the general-purpose op amps examined in Chapter Two included a compensating capacitor. No matter how much feedback we wish to use, our circuits will always end up being stable. For the best circuit performance, it is possible to use amplifiers that do not have the “constant rolloff” characteristic. The possibility exists that they may go into oscillation or become unstable if you are not careful and ignore the margins.
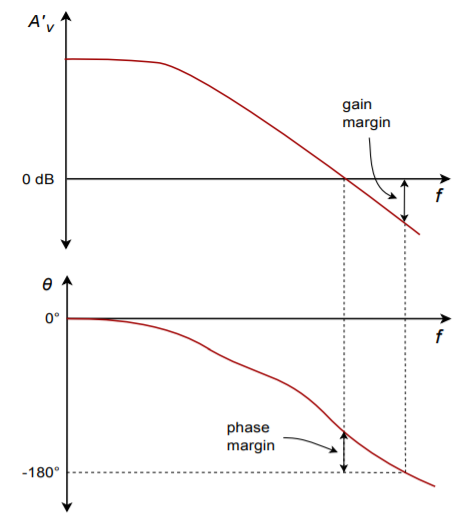
Figure \(\PageIndex{3}\): Gain and phase margin graphically determined from Bode plot.





