Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.3: Relationship Types

Last updated

Jan 3, 2023
Save as PDF
- 9.2: Business Rules
- Chapter 10 - ER Modelling

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

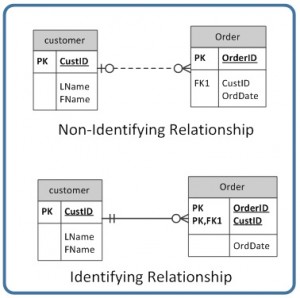
The line that connects two tables, in an ERD, indicates the relationship type between the tables: either identifying or non-identifying. An identifying relationship will have a solid line (where the PK contains the FK). A non-identifying relationship is indicated by a broken line and does not contain the FK in the PK. See the section in Chapter 8 that discusses weak and strong relationships for more explanation.

Figure 9.5. Identifying and non-identifying relationship. — *Figure* $\PageIndex{1}$ : *Identifying and non-identifying relationship, by A. Watt.*

Optional relationships

In an optional relationship, the FK can be null or the parent table does not need to have a corresponding child table occurrence. The symbol, shown in Figure $\PageIndex{2}$ , illustrates one type with a zero and three prongs (indicating many) which is interpreted as zero OR many.

Figure $\PageIndex{2}$ : Zero or Many. ("Zero or Many" by Patrick McClanahan is licensed under CC BY-SA 4.0)

For example, if you look at the Order table on the right-hand side of Figure $\PageIndex{3}$ , you’ll notice that a customer doesn’t need to place an order to be a customer. In other words, the many side is optional.

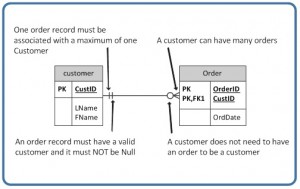
Cardinality-Optional-0-or-more-300x189 — *Figure* $\PageIndex{3}$ : *Example usage of a zero to many optional relationship symbol, by A. Watt.*

The relationship symbol in Figure $\PageIndex{3}$ can also be read as follows:

Left side: The order entity must contain a minimum of one related entity in the Customer table and a maximum of one related entity.
Right side: A customer can place a minimum of zero orders or a maximum of many orders.

Figure $\PageIndex{4}$ shows another type of optional relationship symbol with a zero and one, meaning zero OR one. The one side is optional.

Figure

$\PageIndex{4}$ :

Figure $\PageIndex{5}$ gives an example of how a zero to one symbol might be used.

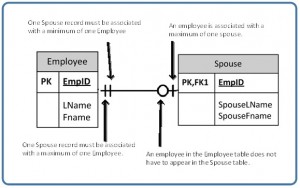
Cardinality-Optional-0-or-1-300x188 — *Figure* $\PageIndex{5}$ : *Example usage of a zero to one optional relationship symbol, by A. Watt.*

Mandatory relationships

In a mandatory relationship, one entity occurrence requires a corresponding entity occurrence. The symbol for this relationship shows one and only one as shown in Figure $\PageIndex{6}$ . The one side is mandatory.

Figure

$\PageIndex{6}$ :

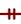
See Figure $\PageIndex{7}$ for an example of how the one and only one mandatory symbol is used.

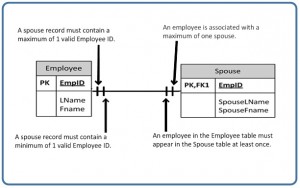
Ch-9-Mandatory-Cardinality-one-to-one-300x188 — *Figure* $\PageIndex{7}$ : *Example of a one and only one mandatory relationship symbol, by A. Watt.*

Figure $\PageIndex{8}$ illustrates what a one to many relationship symbol looks like where the many side is mandatory.

Figure

$\PageIndex{8}$ :

Refer to Figure $\PageIndex{9}$ for an example of how the one to many symbol may be used.

Ch-9-Mandatory-Cardinality-one-to-Many-300x188 — *Figure* $\PageIndex{9}$ : *Example of a one to many mandatory relationship symbol, by A. Watt.*

So far we have seen that the innermost side of a relationship symbol (on the left-side of the symbol in Figure $\PageIndex{10}$ ) can have a 0 (zero) cardinality and a connectivity of many (shown on the right-side of the symbol in Figure $\PageIndex{10}$ ), or one (not shown).

Ch-9-Zero-or-Many-1 — *Figure* $\PageIndex{10}$ :

However, it cannot have a connectivity of 0 (zero), as displayed in Figure $\PageIndex{11}$ . The connectivity can only be 1.

Figure

$\PageIndex11}$ :

The connectivity symbols show maximums. So if you think about it logically, if the connectivity symbol on the left side shows 0 (zero), then there would be no connection between the tables.

The way to read a relationship symbol, such as the one in Figure $\PageIndex{12}$ , is as follows.

The CustID in the Order table must also be found in the Customer table a minimum of 0 and a maximum of 1 times.
The 0 means that the CustID in the Order table may be null.
The left-most 1 (right before the 0 representing connectivity) says that if there is a CustID in the Order table, it can only be in the Customer table once.
When you see the 0 symbol for cardinality, you can assume two things: T
1. the FK in the Order table allows nulls, and
2. the FK is not part of the PK since PKs must not contain null values.

Ch-9-Cust-to-Order-ERD-300x168 — *Figure* $\PageIndex{12}$ : *The relationship between a Customer table and an Order table, by A. Watt.*

Key Terms

business rules: obtained from users when gathering requirements and are used to determine cardinality

cardinality: expresses the minimum and maximum number of entity occurrences associated with one occurrence of a related entity

connectivity: the relationship between two tables, e.g., one to one or one to many

constraints: the rules that force DBMSs to check that data satisfies the semantics

entity integrity: requires that every table have a primary key; neither the primary key, nor any part of it, can contain null values

identifying relationship: where the primary key contains the foreign key; indicated in an ERD by a solid line

integrity constraints: logical statements that state what data values are or are not allowed and which format is suitable for an attribute

mandatory relationship:one entity occurrence requires a corresponding entity occurrence.

non-identifying relationship: does not contain the foreign key in the primary key; indicated in an ERD by a dotted line

optional relationship: the FK can be null or the parent table does not need to have a corresponding child table occurrence

orphan record: a record whose foreign key value is not found in the corresponding entity – the entity where the primary key is located

referential integrity: requires that a foreign key must have a matching primary key or it must be null

relational database management system (RDBMS): a popular database system based on the relational model introduced by E. F. Codd of IBM’s San Jose Research Laboratory

relationship type: the type of relationship between two tables in an ERD (either identifying or non-identifying); this relationship is indicated by a line drawn between the two tables.

Exercises

Read the following description and then answer questions 1-5 at the end.

The swim club database in Figure 9.5.16 has been designed to hold information about students who are enrolled in swim classes. The following information is stored: students, enrollment, swim classes, pools where classes are held, instructors for the classes, and various levels of swim classes. Use Figure 9.5.16 to answer questions 1 to 5.

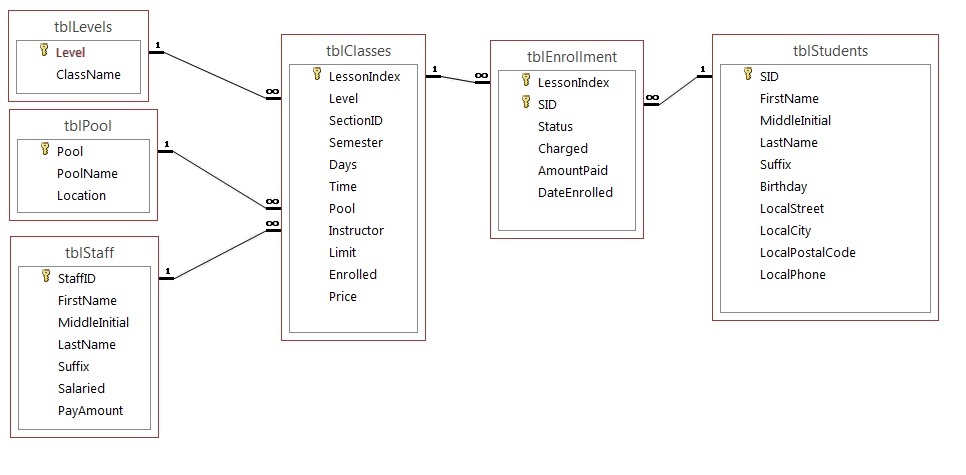
The primary keys are identified below. The following data types are defined in the SQL Server.

tblLevels
Level – Identity PK
ClassName – text 20 – nulls are not allowed

tblPool
Pool – Identity PK
PoolName – text 20 – nulls are not allowed
Location – text 30

tblStaff
StaffID – Identity PK
FirstName – text 20
MiddleInitial – text 3
LastName – text 30
Suffix – text 3
Salaried – Bit
PayAmount – money

tblClasses
LessonIndex – Identity PK
Level – Integer FK
SectionID – Integer
Semester – TinyInt
Days – text 20
Time – datetime (formatted for time)
Pool – Integer FK
Instructor – Integer FK
Limit – TinyInt
Enrolled – TinyInt
Price – money

tblEnrollment
LessonIndex – Integer FK
SID – Integer FK (LessonIndex and SID) Primary Key
Status – text 30
Charged – bit
AmountPaid – money
DateEnrolled – datetime

tblStudents
SID – Identity PK
FirstName – text 20
MiddleInitial – text 3
LastName – text 30
Suffix – text 3
Birthday – datetime
LocalStreet – text 30
LocalCity – text 20
LocalPostalCode – text 6
LocalPhone – text 10

Implement this schema in SQL Server or access (you will need to pick comparable data types). Submit a screenshot of your ERD in the database.

Explain the relationship rules for each relationship (e.g., tblEnrollment and tblStudents: A student can enroll in many classes).
Identify cardinality for each relationship, assuming the following rules:
- A pool may or may not ever have a class.
- The levels table must always be associated with at least one class.
- The staff table may not have ever taught a class.
- All students must be enrolled in at least one class.
- The class must have students enrolled in it.
- The class must have a valid pool.
- The class may not have an instructor assigned.
- The class must always be associated with an existing level.
Which tables are weak and which tables are strong (covered in an earlier chapter)?
Which of the tables are non-identifying and which are identifying?

Optional relationships

Mandatory relationships

Key Terms

Exercises

Support Center

How can we help?