7.2: List five properties of relations

In database systems, there exist relations in a two-dimensional table of data. This typically has multiple named columns and an indeterminate quantity of rows for data to be entered. A common misconception is a database relation being mistaken for a relational database. The main point to remember is that a relation specifically refers to an individual table in a relational database. There are specific properties that define relations so that they can be easily identified by a user. These relations have many properties that identify and separate themselves from non-relational tables. 

Properties of relations: 

1. Each table in a database has a unique identity (name). 
2. Any entry at the connection of each row and column has a single value. There can be only one value that is related with each attribute on a specific row of a table; no multivalued attributes are allowed in a relation. 
3. Each row is unique; no two rows or tables in the same relation can be identical. 
4. Each attribute (or column) within a table has a unique name. 
5. The sequence of columns (left to right) is insignificant. The order of the columns in a relation can be changed without changing the meaning or use of the relation. 
6. The sequence of rows (top to bottom) is insignificant. As with columns, the order of the rows of a relation may be changed or stored in any sequence. 

A few of these properties tie into one another, namely, the first, fourth, and sixth. The columns having unique attributes and the individual rows being arbitrarily organized very simply explains the core properties of relations. 

Figure \(\PageIndex{1}\): Example of Property One. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

The second property speaks to Codd's original notion from 1969 that each and every attribute in individual tuples inside of a relation must only consist of a single value and not allow any different multivalued values of the kind supported in databases. 

Figure \(\PageIndex{2}\): Example of Property Two. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

The third property speaks to the uniqueness within the table itself and how each individual row can only have values of data that are unique to the row itself. This ensures that no two rows will be identical. 

Figure \(\PageIndex{3}\): Example of Property Three. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

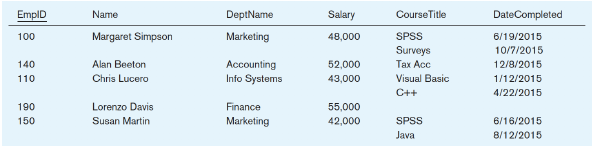
The fifth property specifically describes how the order does not matter in regard to the columns themselves. In Figure \(\PageIndex{3}\), the order of columns can be arbitrary in the structure itself. 

Entities, Relations, and Characteristics 

• Each row contains data about an entity (table). 
• Each column contains data related to attributes of the entities. 
• All entries in a column are of the same kind. 
• Each cell of the table holds a single value. 
• The order of the columns is not important. 
• The order of the rows is not important 
• No two rows may be identical. 

EmpolyeerNumber	FirsName	LastName	Department	EmailAddress	PhoneNum
10	Judy	Griffin	Payroll	[e-mail]	780-492-5689
20	Lily	Murphy	Security	[e-mail]	305-129-4593
30	Sam	Moore	Accounting	[e-mail]

Table \(\PageIndex{1}\): Entities Relations Characteristics. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

Table 2 below shows three columns: the buyer’s name, the SKU (stock keeping unit), and the names of the buyer’s college major. The Buyers_Name may be associated with more than one SKU, and they can have multiple Departments. 

	Buyers_Name	SKU_Numbers	Department
1	Judy Griffin	Griffin	Payroll
2	Lily Murphy	Murphy	Security
3	Sam Moore	Moore	Accounting

Table \(\PageIndex{2}\): Buyer and SKU_Numbers. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

In the relational model of Databases: 

• A candidate key is an element that controls all the other columns in a relation. The SKU_DATA relation has two candidate keys: SKU and SKU_Description. Buyer is an element, but it is not a candidate key because it controls only Department. 
• A primary key is a specific choice of a minimal set of attributes (Columns) that is a single row of a table in a database relation. A table has only one primary key. The primary key can have one column, or it can be a composite. The definition of a table is given as (SKU, SKU_Description, Department, Buyer), where SKU is the primary key of SKU_DATA and the (OrdrNumber, SKU) is the primary key of ORDER_ITEM. 
• A surrogate key is an artificial column that is added to a table to serve as the primary key when the primary key is large. RENTAL_PROPERTY is the relationship below. 
• A foreign key is a column that is the primary key of a table. The term occurs because it is a key of a table foreign to the one in which it appears as the primary key. In the below two tables, COMPANY.CompanyName is the primary key of COMPANY, and EMPLOYEE.Company is a foreign key. In this text, we will show foreign keys in italics: 
• Anomalies are problems that can occur in poorly planned database systems, unnormalised databases where the majority of the data are stored in one table (a flat-file database). An Insertion Anomaly may be such that it is not possible to add a required piece of data unless another piece is unavailable data that is removed. When we delete one row, the structure of this table forces to lose facts about two different things: a machine and a repair. This condition is called a deletion anomaly.