9.2: Activity 2 - Sorting Algorithms by selection method
- Page ID
- 47932
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This activity will present two selection based sorting algorithms, the selection sort and the heap sort algorithms.
Activity Details
Selection sort
The selection sort algorithm works by repeatedly exchanging elements: first finds the smallest in the array and exchange it with the element in the first position, then find the second smallest element and exchange it with the element in the second position, and continue in this way until the entire array is sorted. Below we present the selection sort algorithm:
SELECTION_SORT (A)
for i ← 1 to n-1 do
min j ← i;
min x ← A[i]
for j ← i + 1 to n do
If A[j] < min x then
min j ← j
min x ← A[j]
A[min j] ← A [i]
A[i] ← min x
Selection sort is among the simplest of sorting techniques and it work very well for small files. Furthermore, despite its evident “simplistic approach”, selection sort has a quite important application because each item is actually moved at most once, thus selection sort is a method of choice for sorting files with very large objects (records) and small keys. Below we present the selection sort implementation:
void selectionSort(int numbers[], int array_size)
{ int i, j;
int min, temp;
for (i = 0; i < array_size-1; i++)
{ min = i;
for (j = i+1; j < array_size; j++)
{ if (numbers[j] < numbers[min])
min = j; }
temp = numbers[i];
numbers[i] = numbers[min];
numbers[min] = temp; }
The complexity of the selection sort algorithm is as follows. The worst case occurs if the array is already sorted in descending order. Nonetheless, the time required by selection sort algorithm is not very sensitive to the original order of the array to be sorted: the test “if A[j] < min x” is executed exactly the same number of times in every case. The variation in time is only due to the number of times the “then” part (i.e., min j ← j; min x ← A[j] of this test are executed. Selection sort is quadratic in both the worst and the average case, and requires no extra memory.
Note that for each i from 1 to n - 1, there is one exchange and n - i comparisons, so there is a total of n -1 exchanges and (n -1) + (n -2) + . . . + 2 + 1 = n(n -1)/2 comparisons. These observations hold no matter what the input data is. In the worst case, this could be quadratic, but in the average case, this quantity is O(n log n). It implies that the running time of selection sort does not depend on how the input may be organized.
Heaps Sort
We can use heap for sorting a collection in a specific order efficiently. Suppose we want to sort elements of array Arr in ascending order. We can use max heap to perform this operation through the following steps:
- Build a max heap of elements in Arr.
- Now the root element, Arr[1], contains maximum element of Arr. Exchange this element with the last element of Arr and again build a max heap excluding the last element which is already in its correct position. Thus decreases the length of heap by one.
- Repeat step (ii) until all elements are in their correct position.
- Get a sorted array.
In the following the implementation of heap sort algorithm is provided (Assuming there are N elements stored in array Arr):
void heap_sort(int Ar[ ])
{ int heap_size = N;
build_maxheap(Arr);
for(int i = N; i>=2 ; i-- )
{ swap|(Arr[ 1 ], Arr[ i ]);
heap_size = heap_size-1;
max_heapify(Arr, 1, heap_size); }
The time complexity of the heap-sort algorithm is as follows: Recall from Chapter 8 that max_heapify has complexity O(logN), build_maxheap has complexity O(N) and the fact that the algorithm calls max_heapify N-1 times, therefore the complexity of heap_sort function is O(N logN).
We now demonstrate the steps of the heap sort algorithm using an example of an unsorted array Arr having 6 elements and corresponding max-heap as in Figure \(\PageIndex{1}\).
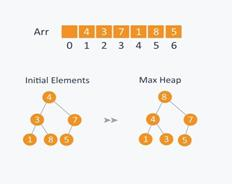
After building the corresponding max-heap, the elements in the array Arr are now as in Figure \(\PageIndex{2}\).

The subsequent algorithm processing steps are outlined below and further depicted in Figure \(\PageIndex{3}\).
- 8 is swapped with 5.
- 8 is disconnected from heap as 8 is in correct position now and.
- Max-heap is created and 7 is swapped with 3.
- 7 is disconnected from heap.
- Max heap is created and 5 is swapped with 1.
- 5 is disconnected from heap.
- Max heap is created and 4 is swapped with 3.
- 4 is disconnected from heap.
- Max heap is created and 3 is swapped with 1.
- 3 is disconnected.
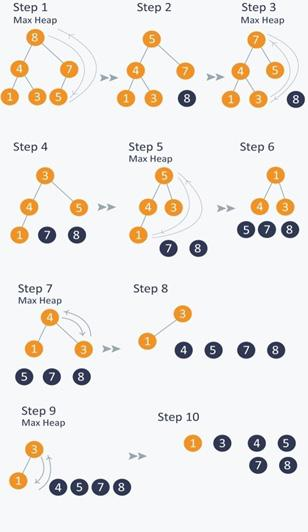
Upon completion of all the steps, we obtain a sorted array shown in Figure \(\PageIndex{4}\).

Conclusion
In this activity the selection based sorting algorithms were presented, the selection sort and the heap sort. The complexity analysis for the two algorithms shows that the heap sort is more efficient, since the selection sort has a quadratic worst case performance. The selection sort is suited to sorting small collections, and the order of input does not influence its performance.
Assessment
- Show the steps taken when sorting the following list of integers [80, 30, 50, 70, 60, 90, 20, 30, 40] using
- Selection sort


