9.3: Statistical Plots

By Carey A. Smith

Two types of plots to visualize statistical data are the histogram and the boxchart. To illustrate how to create these, we generate a vector of normally distributed random data with a nominal mean of 50 and a nominal standard deviation of 8.

Example \(\PageIndex{1}\) MATLAB histogram()

This example is only for MATLAB.

The next example is the version for Octave

%% A Histogram is useful for showing the spread of a data set and the frequencies of possible values.

% Examples are ages, blood pressure, home prices, incomes, etc.

% We begin by creating a vector, v4, of random values with a nominal mean and standard deviation:

v4_mean0 = 50;

v4_std0 = 8;

v4 = v4_mean0 + v4_std0*randn(1,100);

% Next we compute the actual mean and standard deviation of the created data vector:

v4_mean1 = mean(v4)

v4_std1 = std(v4)

figure

histogram(v4)
grid on;

% Display the mean and standard deviation in the title with 3 significant figures

title(['Histogram: mean= ',num2str(v4_mean1,3),', std.dev.= ',num2str(v4_std1,3)])

% The histogram's bin edges can be set to any custom values you want.

% This code creates a a set of bin edges from -4 standard deviations to +4 standard deviations, in increments of 1 standard deviation.

h_edges = v4_std0*(-4:4) + v4_mean0

figure

histogram(v4, h_edges)

grid on;

title(['Histogram of v4 with custom bin edges, mean= ',num2str(v4_mean1,3),', std.dev.= ',num2str(v4_std1,3)])

% Displays the mean and standard deviation with 3 significant figures.

Solution

Add example text here.

.

Example \(\PageIndex{2}\) Octave hist()

This example is only for Octave.

%% For Octave, you need to load a graphics tool kit and use the older function hist(x):

graphics_toolkit("fltk") % Needed for Octave 7.2
v4_mean0 = 50;
v4_std0 = 8;
v4 = v4_mean0 + v4_std0*randn(1,100);
% Next we compute the actual mean and standard deviation of the created data vector:
v4_mean1 = mean(v4)
v4_std1 = std(v4)
%% For Octave use the older function hist():
figure
hist(v4)
grid on

% Display the mean and standard deviation in the title with 3 significant figures
title(['hist(): mean= ',num2str(v4_mean1,3),', std.dev.= ',num2str(v4_std1,3)])

%% The histogram's bin centers can be set to any custom values you want.
% This code creates a a set of bin centers from -3.5 standard deviations to +3.5 standard deviations, in increments of 1 standard deviation.
h_centers = v4_std0*(-3.5:3.5) + v4_mean0
figure
hist(v4, h_centers)
grid on;
title(['hist() with custom bin centers, mean= ',num2str(v4_mean1,3),', std.dev.= ',num2str(v4_std1,3)])
% Displays the mean and standard deviation with 3 significant figures.
 

Solution

Add example text here.

.

Exercise \(\PageIndex{1}\)Mimic 100 dice rolls

Assignment histogram: Mimic 100 dice rolls, plot a histogram, compute the mean and standard deviation

(a) Create a vector with 100 uniform random integers between 1 and 6 with this command:

dice = randi(6, 1, 100); % randi generates random integers

(b) Set the bin edges to be

bin_edges= 0.5 : 1 : 6.5;

Plot a histogram of the data using this bin_edges vector.

(c) Compute mdice = the mean of the vector dice
Compute sdice = the standard deviation of the vector dice
Write the mean and standard deviation in the title using this line of code:
title(['100 Dice Rolls, Mean= ' , num2str(mdice) , ' , Std. Dev.= ' , num2str(sdice)]);

You may want to repeat this a few times, to see how it varies as the random number vector is regenerated.

Answer

One iteration looks like this:

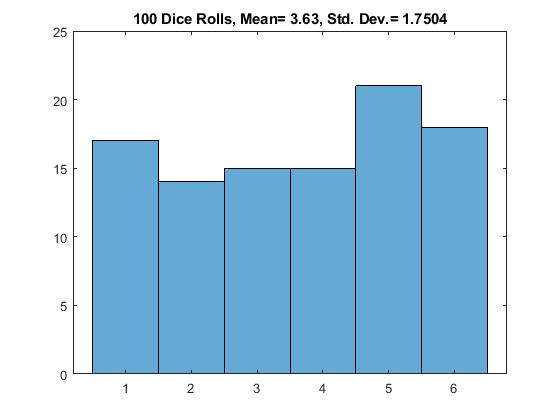
Figure \(\PageIndex{1}\): Historgram Example: Mimic 100 dice rolls

Boxchart (a.k.a. boxplot)

%% A boxchart is another plot of the data.

% It is often used for data that is not normally distributed. It shows the following:

• minimum
• 25th-percentile (1st quartile or Q1)
• median (50th-percentile)
• 75th-percentile (3rd quartile or Q3)
• maximum

Example \(\PageIndex{3}\) boxplot

This example code shows you how to create a MATLAB boxplot.

load patients % This is a built-in sample file with various data
n = length(Age) % Number of patients
figure('Name','boxchart() Example')
boxchart(Age)
title('Patient''s Ages')
ylabel('Age (years)')
xlabel([num2str(n),' Patients'])
ylim([20,60])
Age_min = min(Age)
Age_median = median(Age)
Age_max = max(Age)
text(1,(Age_min+1), ['min= ',num2str(Age_min)])
text(1,(Age_median+1),['median= ',num2str(Age_median)])
text(1,(Age_max+1), ['max= ',num2str(Age_max)])

Solution

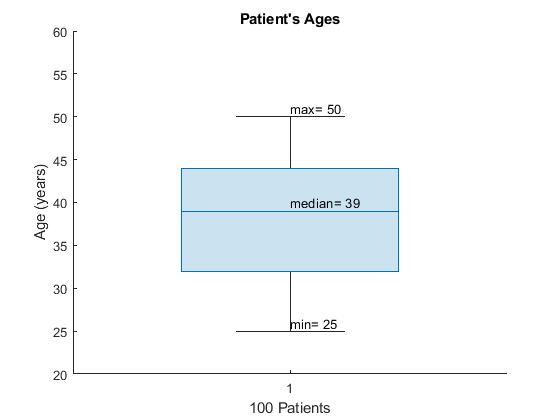
Figure \(\PageIndex{2}\): Boxchart example of patients' ages

Note: Matlab creates vertical boxplots. Books and other software typically create horizontal boxplots. The same information is shown in both types.