11.3: Using fzero() to find the intersection of 2 functions

Using fzero() to find the intersection of 2 functions

Assume you have functions y1(x) and y2(x). Create a new function y3(x) = y1(x) - y2(x). The zero of y3(x) is the intersection of y1(x) and y2(x).

Example \(\PageIndex{1}\) Find the intersection of cos(2x) and 3x

We will have 4 files. A test script file, and 3 function files: function files for each of the 2 functions and a function file that computes the difference of the 2 functions.

% A1. Create a file for a function that computes this straight line:

function y1 = fcn_line_03x(x)
    y1 = 0.3*x;
end

% A2. Create a file for a function that computes this cosine function:

function y2 = cos2x(x);
    y2 = cos(2*x);
end

B. Create a function that computes the difference of these 2 functions:

function y3 = fcn_line_cos_diff(x)
    y3 = fcn_line_03x(x) - cos(2*x);
end
 

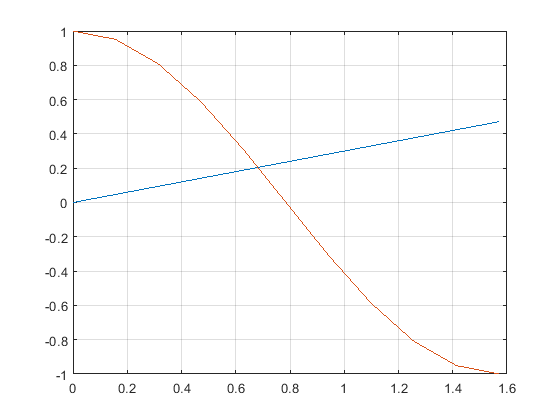
C. The test script m-file call the 2 functions in parts A1 and A2, opens a new figure, and plots the 2 functions:

x = (0: 0.02: 0.5)*pi;
y1 = fcn_line_03x(x);
y2 = cos(2*x);
figure(1)
plot(x,y1)
hold on;
plot(x,y2,'-s')
grid on;
axis equal

% We can see that one intersection of these functions is near x = 0.7 and y = 0.2

D. At the intersection point, y1(x) = y2(x). Rearranging, we get y1(x)- y2(x) = 0. 

Create a function file that computes the difference between the 2 functions.

function y3 = fcn_line_cos_diff(x)
    y3 = fcn_line_03x(x) - cos(2*x);
end
 

So, were can use fzero() to find the point where the difference of the 2 functions is zero.

The code in the test script is:

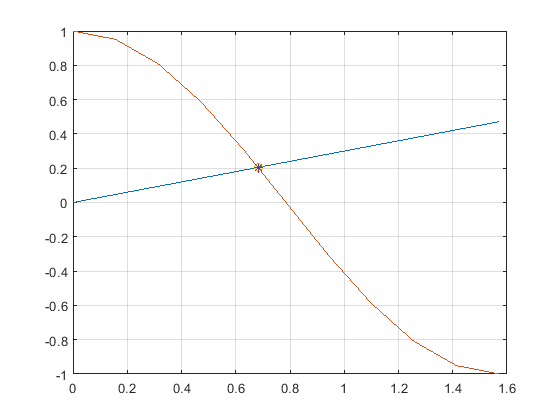
x_solution = fzero(@fcn_line_cos_diff, 0.7) % near 0.7

% 0.6823

% Verify that this is a solution:

% Verify that this is a solution
y1b = fcn_line_03x(x_solution) % 1st function
% 0.2047
y2b = cos2x(x_solution) % 2nd function
% 0.2047

%% Plot the solution point on the 1st figure
figure(1)
hold on;

plot(x_solution,y1b,'bo','Markersize', 10)
plot(x_solution,y2b,'c*','Markersize', 10)

Exercise \(\PageIndex{1}\)

Add exercises text here.

Answer

Add texts here. Do not delete this text first.

Solution

Add example text here.

.

Exercise \(\PageIndex{1}\) Intersection of quadratic and cubic functions

A. (2 pts) Create these 2 function files:

y_fun_x2(x)
   y_x2 = x.^2 -4;

end

function y_x3 = y_fun_x3(x)
   y_x3 = x.^3 - 6*x;
end

B1. (2 pt) Begin a script m-file named fzero_y_fun_x2_x3_YourName.m that will plot these functions and will solve for one of their intersections.

At the top of this script, include this code:

clear all; clear functions; close all; format compact; clc; 

B2a. (1 pt) Create an x vector from -3 to 3
Choose an increment for x = 0.3, so that the plot will be smooth.
B2b. (2 pts) Use this x vector to compute the corresponding values of y for each of the 2 functions.

y2 = y_fun_x2(x);
y3 = y_fun_x3(x);

B3. (2 pts) Open a figure and plot y2, add "hold on;", the plot y3 on the figure. You will see that they intersect at 3 places.

C1. (2 pts) fzero() finds a root of a single function, so create a 3rd function that computes the difference of the 1st 2 functions:

function y23 = y_2_3_fun(x) 
   y23 = y_fun_x2(x) - y_fun_x3(x);
end

Use the x vector to compute values of y for the difference function:

y23 = y_2_3_fun(x)

C2. (1 pt) Open a 2nd figure and plot(x, y23)

D. (6 pts) Use the fzero() function to find a solution where y_2_3_fun(x) = 0.

Use the function handle, @y_2_3_fun as the 1st input of fzero().

For the initial value of x, choose an integer value (whole number) near any one of the intersection points. (Do not use a decimal value that is not an integer.)

Answer

Add texts here. Do not delete this text first.

.

Exercise \(\PageIndex{2}\) fzero_exp

A. Set

x = (0 : 0.05 : 1)

B. Compute these 2 functions:

y1 = 0.7x

y2 = exp(-2*x)

C. Open a new figure and plot these 2 functions on it.

plot(x,y1)

hold on;

plot(x,y2)

The intersection of these 2 functions is the solution of this transcendental equation:

y1 = y2 or, equivalently, y1 - y2 = 0

D. Find the value of x near 0.5 that is a solution of this equation using the fzero() function as follows:

D1. Rewrite it in the form: fexp(x) = exp(-2*x) - 0.7*x, then create a function file called fexp.m that computes this.

D2. Solve it using the fzero() function, using @fexp as the function handle. 

Answer

Add texts here. Do not delete this text first.

.