2.2.4.6: Extreme Tidal Effects
- Page ID
- 84588
The tidal effects seen on Earth can be thought of as "moderately strong". Note that such effects are inversely proportional to the \textbf\textit{cube} of the distance to the body responsible for them. Therefore, if the distance were halved, the tidal effects' power would increase as much as eightfold!
Well, the Earth-Moon and the Earth-Sun average distances are very stable, so the magnitude of the tidal effects on Earth is not going to change in the current epoch. However, there are celestial bodies ibn the Solar System that experience much stronger tidal effects than Earth -sometimes strong enough that they can even lead to “catastrophic'' results. It may be instructive to consider such a scenario in somewhat closer detail.
Suppose that there is a satellite of mass \(m\) and radius \(d\), orbiting a planet of mass \(M\) at a distance of \(r\). Now we will use the same two hemispheres which we considered before for deriving the equation for the magnitude of the tidal forces. With one small change -since the \(m\) symbol has been already “taken'' for the satellite mass, let's use the Greek equivalent instead -i.e., let the mass of each hemisphere be \(\mu/2\).
In the preceding Section, we considered two hemispheres, \(2d\) apart, coupled by a spring. Let's now put them on the surface of the satellite, one at the point closest to the planet and the other at the point most distant from it -as is shown in the Figure 2.5. Just put them, but we don't want to attach them to the surface by any constraints.
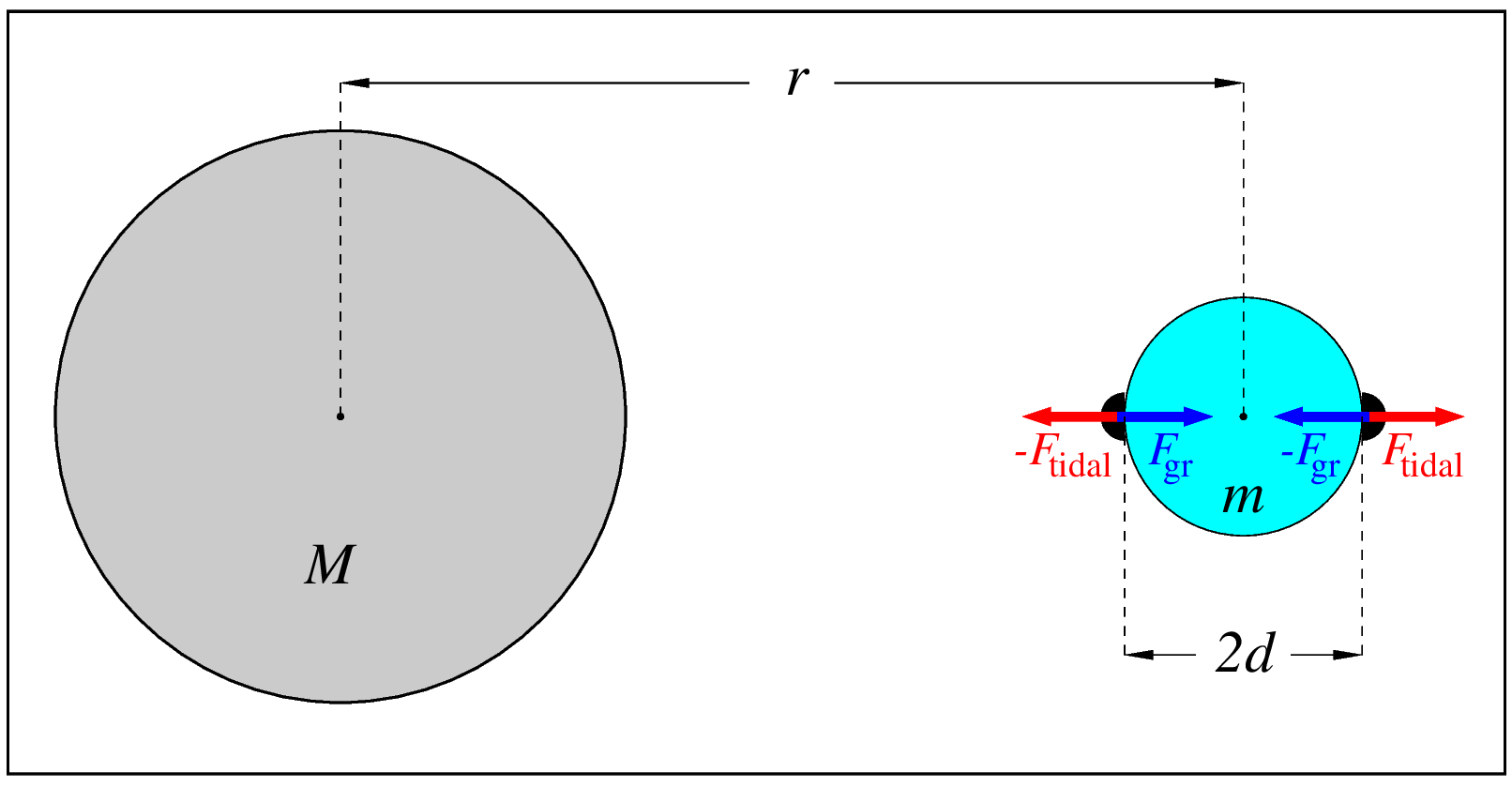
So, we have now the two hemispheres \(2d\) apart. Both are pulled “inwards'', i.e., towards the middle point,
but not by the stretched spring force as before -now, by the gravity of the satellite, \(\pm F_{gr}\) (in the Figure 2.5, the positive direction is, conventionally, from the left to the right). The magnitude of this force is:
\[ F_{gr} = G\frac{\frac{\mu}{2}\cdot m}{d^2}\]
This is the effect of the satellite's “own'' gravity. But there is also gravity “supplied'' by the planet. And as we know from the preceding section, two hemispheres, \(2d\) apart, falling freely in a gravitational field of a planet, experience a tidal force tending to “stretch'' the pair -i.e., acting upon each of them with an “outwards-directed'' force \( \pm F_{tidal}\), as shown in the Fig. 2.5. The magnitude of this force is given by the Eq. 2.56:
\[ F_{tidal} = G\frac{\mu \cdot M}{r^3}d\]
As opposed to \(F_{gr}\) which is constant, the \(F_{tidal}\) force depends on the satellite-planet distance \(r\) -it increases with decreasing distance, and for certain value of \(r\) the \(F_{tidal}\) force may become equal to \(F_{gr}\). This \(r\) value is called “the Roche Limit'' in honor of the French astronomer Edouard Albert Roche, who first considere the effects of strong tidal forces on celestial bodies. By equating the Eqs. 2.57 and 2.58 and solving for \(r\), one obtains the formula for the Roche Limit:
\[ G\frac{\mu \cdot M}{r^3}d = G\frac{\frac{\mu}{2}\cdot m}{d^2}\;\;\;\; \Longrightarrow \;\;\;\; r_{Roche} = d\sqrt[3]{\frac{2M}{m}}\]
What happens if the satellite gets even closer to the planet than the Roche Limit? Well, the tidal force will become dominant. The hemisphere closer to the planet will start falling towards the planet. Paradoxically, the other hemisphere will take off from the moon's surface and... fly up!
If the satellite comes even closer to the planet, not just objects loosely lying on the surface will be detached from it, but whole blocks of matter will be ripped off from the satellite -such a process is illustrated by a series of slides in the Wikipedia article titled Roche Limit.
It is commonly accepted that the famous rings of Saturn were created by tidal forces that “pulverized'' a satellite that got closer to the planet than the Roche Limit. Anather spectacular manifestation of destructive tidal forces was the fragmentation of the Shoemaker-Levy 9 comet}, ''captured'' by Jupiter -eventually, in June 1994, the fragments, one after another, collided with the planet, creating spectacular fireballs on its surface.
For Moon whose mean radius \(d = 1,738\) km, and mass is 1/81 of the Earth mass, the Eq. 2.48 yields a Roche Limit of about 9,500 km. Note that Roche Limit is the distance between the centers of the two bodies in question: accordingly, since the mean Earth's radius is 6,356 km, the distance between the surfaces of Earth and of Moon at the Roche Limit would be only (9,500 6,356 1,738) km = 1,406 km -very, very close. The rocks ripped out from Moon would then surely “bombard'' Earth. Fortunately, though, the Moon's position is 40 times farther away from Earth than the Roche Limit, and this distance is even slowly increasing (about 1.5 inch/year), so there is no danger that such a “bombardment'' will ever happen.

