6: Windpower
- Page ID
- 84600
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Wind power is nothing else than converted solar power (as is, e.g., hydropower, windpower, wavepower, or the power generated by burning biofuels).
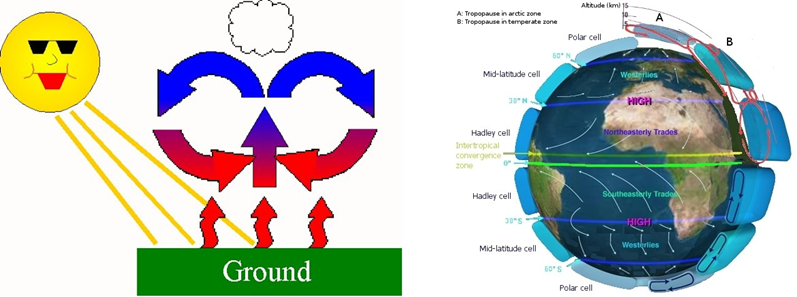
In general, wind is caused by the fact that different areas on the Earth surface get heated up at different rate by sunshine (or the rate of cooling after the sunset is different).
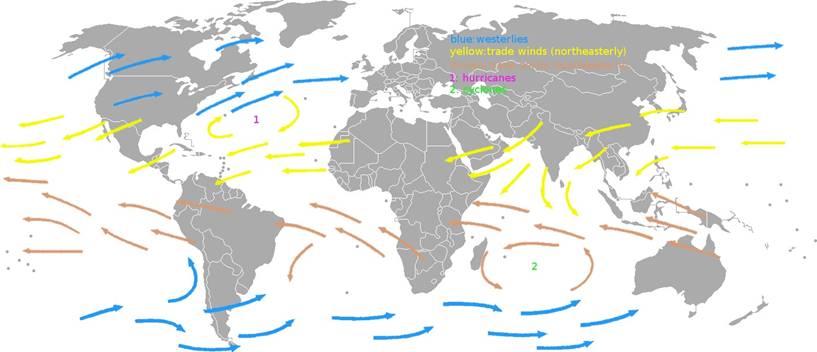
One well-known example a winds which are always blowing over the oceans in the same direction are the trade winds (a.k.a. passats) One is blowing between the Equator and the 30th parallel north1 from the North- East and is called the Northeasterly Trade Wind. The other is blowing and between the Equator and the 30th parallel from the South-East and is called the Southeasterly Trade Wind.
Both these trade winds are caused by hot air rising in the vicinity of Equator. The air “escaping up” leaves behind a “void”, i.e., an area of low pressure. When reaching the troposphere, the rising-up stream of air splits into two, one moving north, and the other moving south. At high altitude, the air cools down, gets heavier, and eventually falls back towards the the Earth surface in the vicinity of the 30th parallel north and the 30th parallel south, causing an increase of the air pressure in both these areas. So, the air starts moving from them towards the area of lower pressure, i.e., towards the Equator.
The above description may suggest that both winds blow directly towards the Equator from the North ans from the South. And, as was stated earlier, actually they blow from the North-East and from the South-East. How come? Well, there is yet another factor involved, called the Coriolis Force.
The Earth, as we all know, is a rotating body. The forces acting on objects in rotating systems are described by Newtonian Mechanics. There are two such forces – the centrifugal force acting on objects which are fixed in the rotating system (we all know from this force from rides in a merry-go-round), and the Coriolis force which acts on objects moving in the rotating system. The winds are moving objects, so it is the Coriolis force they experience. The general theory of the Coriolis force is a bit complicated – but it is not necessary to study it in detail, a simplified explanation is all we need.
First, consider the speed of a fixed point at the Equator. Its circumference is about 40 000 km. The Earth makes one revolution in 24 hours, or in 24 3600 s = 86400 s. So, the speed of a point at the Equator is (40000 km)/(86400 s) = 463 m/s. The Earth is rotating from the West to the East, so it is 463 m/s in the eastern direction.
Now, consider a point at the 30th parallel. This parallel is a circle of circumference equal to (40000 km) cos 30◦ = 34641 km. By dividing it by 86400 s, we get the speed of 401 m/s. The air starting its trip towards the Equator moves then with a speed of 401 m/s eastbound – but the point at the Equator is moving faster by 62 m/s in the same direction. So, the wind is “lagging behind” and when it finally reaches the Equator, it is at a point that are pretty more to the West than the point from which it started its trek. Consequently, an observer at the Equator will see a wind coming from the North-East, not straight from the North –or coming from the South-East, not directly from the South.
But this is not the end. Not all air descending from above near the 30th parallel would attempt to travel towards the Equator – some will floe in the opposite direction, to the North or to the South. The Coriolis Force will then push the wind in westbound. So, above and under thea areas where the North-East and South-East trade wind blow, there are winds blowing from the South-West and North-West. Such winds were called westerlies by anglo-saxon sailors, and anti-passates by German and Dutch sailors.
___________________________________________________
1The 30th parallel north is a circle of latitude that is 30 degrees north of the Earth’s equatorial plane.