4.6: Encoding Information in the Frequency Domain
- Page ID
- 1618
- Using a finite Fourier series to represent the encoding of information in time T.
To emphasize the fact that every periodic signal has both a time and frequency domain representation, we can exploit both to encode information into a signal. Refer to the Fundamental Model of Communication. We have an information source, and want to construct a transmitter that produces a signal x(t). For the source, let's assume we have information to encode every T seconds. For example, we want to represent typed letters produced by an extremely good typist (a key is struck every T seconds). Let's consider the complex Fourier series formula in the light of trying to encode information.
\[x(t)=\sum_{k=-K}^{K}c_{k}e^{i\frac{2\pi kt}{T}} \nonumber \]
We use a finite sum here merely for simplicity (fewer parameters to determine). An important aspect of the spectrum is that each frequency component ck can be manipulated separately: Instead of finding the Fourier spectrum from a time-domain specification, let's construct it in the frequency domain by selecting the ck according to some rule that relates coefficient values to the alphabet. In defining this rule, we want to always create a real-valued signal x(t). Because of the Fourier spectrum's properties, the spectrum must have conjugate symmetry. This requirement means that we can only assign positive-indexed coefficients (positive frequencies), with negative-indexed ones equaling the complex conjugate of the corresponding positive-indexed ones.
Assume we have N letters to encode: {a1,...,aN}. One simple encoding rule could be to make a single Fourier coefficient be non-zero and all others zero for each letter. For example, if an occurs, we make:
\[c_{n}=1\; and\; c_{k}=0,\; k\neq n \nonumber \]
In this way, the nth harmonic of the frequency 1/T is used to represent a letter. Note that the bandwidth—the range of frequencies required for the encoding—equals N/T. Another possibility is to consider the binary representation of the letter's index. For example, if the letter a13 occurs, converting 13 to its base 2 representation, we have 13=11012. We can use the pattern of zeros and ones to represent directly which Fourier coefficients we "turn on" (set equal to one) and which we "turn off".
Compare the bandwidth required for the direct encoding scheme (one nonzero Fourier coefficient for each letter) to the binary number scheme. Compare the bandwidths for a 128-letter alphabet. Since both schemes represent information without loss -- we can determine the typed letter uniquely from the signal's spectrum -- both are viable. Which makes more efficient use of bandwidth and thus might be preferred?
Solution
N N signals directly encoded require a bandwidth of N/T. Using a binary representation, we need:
\[\frac{log_{2}N}{T} \nonumber \]
For N=128, the binary-encoding scheme has a factor of
\[\frac{7}{128}=0.05 \nonumber \]
smaller bandwidth. Clearly, binary encoding is superior.
Can you think of an information-encoding scheme that makes even more efficient use of the spectrum? In particular, can we use only one Fourier coefficient to represent N letters uniquely?
Solution
We can use N different amplitude values at only one frequency to represent the various letters.
We can create an encoding scheme in the frequency domain to represent an alphabet of letters. But, as this information-encoding scheme stands, we can represent one letter for all time. However, we note that the Fourier coefficients depend only on the signal's characteristics over a single period. We could change the signal's spectrum every T as each letter is typed. In this way, we turn spectral coefficients on and off as letters are typed, thereby encoding the entire typed document. For the receiver (see the Fundamental Model of Communication) to retrieve the typed letter, it would simply use the Fourier formula for the complex Fourier spectrum for each T-second interval to determine what each typed letter was. Figure 4.6.1 shows such a signal in the time-domain.
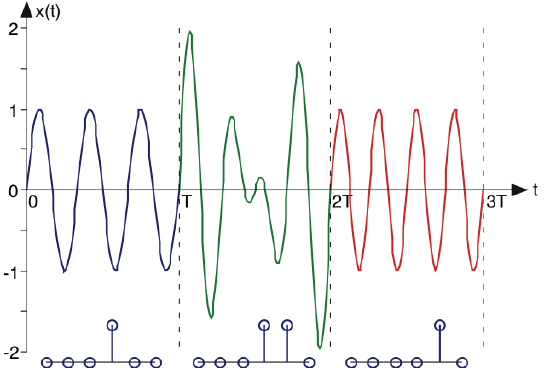
In this example, only the third and fourth harmonics are used, as shown by the spectral magnitudes corresponding to each T-second interval plotted below the waveforms. Can you determine the phase of the harmonics from the waveform?
In this Fourier-series encoding scheme, we have used the fact that spectral coefficients can be independently specified and that they can be uniquely recovered from the time-domain signal over one "period." Do note that the signal representing the entire document is no longer periodic. By understanding the Fourier series' properties (in particular that coefficients are determined only over a T-second interval, we can construct a communications system. This approach represents a simplification of how modern modems represent text that they transmit over telephone lines.


