2.5.2: Debye Length
- Page ID
- 2775
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Equilibrium of Diffusion and Field Currents
Nernst law is a special answer to the general and important question:
How do charged and mobile particles redistribute themselves in an electrical potential if there are some restrictions to the obvious solution that they all move to one or the other pole of the field?
- It is the answer to this question that governs not only pn-junctions, but also batteries, fuel cells, or gas sensors, and, if you like, simply all junctions.
Let us consider a material that essentially contains mobile carriers of only one kind, i.e. a metal (electrons) , a (doped) semiconductor (electrons or holes, depending on doping), or a suitable ionic conductor (one kind of mobile ion).
- We imagine that we hold a positively charged plate at some (small) distance to the surface of a material having mobile negative charges (a metal, a suitable ionic conductor, a n-doped semiconductor, ...). In other words, the positively charged plate and the material are insulated, and no currents of any kind can flow between the two. However, there will be an electrical field, with field lines starting at the positive charges on the plate and ending on the negative charges inside the material. We have the following situation:
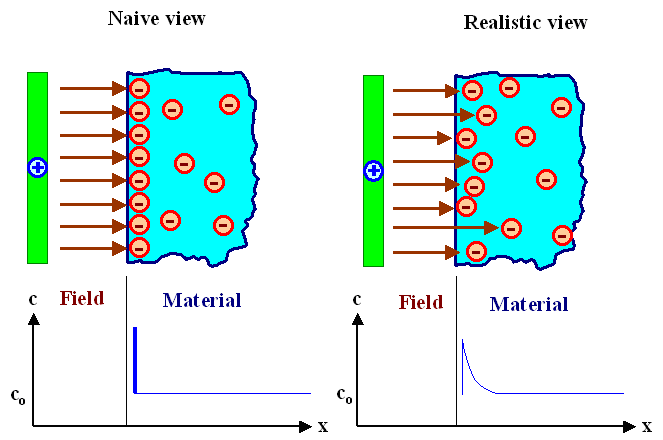
In a naive (and wrong) view, enough negatively charged carriers in the material would move to the surface to screen the field completely, i.e. prevent its penetration into the material. "Enough", to be more precise, means just the right number so that every field line originating from some charge in the positively charged plate ends on a negatively charged carrier inside the material.
- But that would mean that the concentration of carriers at the surface would be pretty much a δ- function, or at least a function with a very steep slope. That does not seem to be physically sensible. We certainly would expect that the concentration varies smoothly within a certain distance, and this distance we call Debye length right away.
- As you might know, the Debye length is a crucial material parameter not only in all questions concerning ionic conducitvity (the field of "Ionics"), but whenever the carrier concentration is not extremely large (i.e. comparable to the concenetration of atoms, i.e in metals).
We will now derive a simple formula for the Debye length. We start from the "naive" view given above and consider its ramifications:
- If all (necessarily mobile) carriers would pile up at the interface, we would have a large concentration gradient and Ficks law would induce a very large particle current away from the interface, and, since the particles are charged, an electrical current at the same time! Since this electrical diffusion current jel, Diff is proportional to the concentration gradient –grad (c(x)), we have:
\[j_{\text{el, Diff}}(x)=-q\cdot D \cdot \text{grad(c(x))}\]
- With D = diffusion coefficient. Be clear about the fact that whenever you have a concentration gradient of mobile carriers, you will always have an electrical current by necessity. You may not notice that current because it might be cancelled by some other current, but it exists nevertheless.
The electrical field E(x), that caused the concentration gradient in the first place, however, will also induce an electrical field current (also called drift current) jfield(x), obeying Ohms law in the most simple case, which flows in the opposite direction of the electrical diffusion current. We have:
\[j_{\text{field}}(x)=q\cdot c \cdot \mu \cdot {\color{purple}E}(x)\]
- With µ = mobility, q = charge of the particle (usually a multiple of the elementary charge e of either sign); q · c · µ, of course, is just the conductivity σ
- The total electrical current will then be the sum of the electrical field and diffusion current.
In equilibrium, both electrical currents obviously must be identical in magnitude and opposite in sign for every x, leading for one dimension to
\[q\cdot c(x) \mu \cdot {\color{purple}E}(x)=q\cdot D \cdot \dfrac{\text{d}c(x)}{\text{d}x}\]
Great, but too many unknowns. But, as we know (????), there is a relation between the diffusion coefficient D and the mobility µ that we can use; it is the Einstein-Smoluchowski relation (the link leads you to the semiconductor Hyperscript).
\[\mu=\text{e}\cdot \frac{D}{\text{k}T}\]
- We also can substitute the electrical Field E(x) by – dU(x)/dx, with U(x) = potential (or, if you like, voltage) across the system. After some reshuffling we obtain
\[-e\frac{\text{d}U(x)}{\text{d}x}=\dfrac{\text{k}T}{c(x)}\cdot \dfrac{\text{d}c(x)}{\text{d}x} =\text{k}T\cdot \frac{\text{d}[\text{ln}(c(x))]}{\text{d}x}\]
- We used the simple relation that d (lnc(x)) / dx = 1/c(x) · dc(x)/dx. This little trick makes clear, why we always find relations between a voltage and the logarithm of a concentration.
- This is a kind of basic property of ionic devices. It results from the difference of the driving forces for the two opposing currents as noted before: The diffusion current is proportional to the gradient of the concentration whereas the field current is directly proportional to the concentration.
Integrating this simple differential equation once gives
\[U(x)+\frac{\text{k}T}{\text{e}}\cdot \text{ln(c(x)) = const.}\]
- Quite interesting: the sum of two functions of x must be constant for any x and for any functions conceivable; the above sum is obviously a kind of conserved quantity.
- That's why we give it a name and call it the electrochemical potential Vec (after muliplying with e so we have energy dimensions). While its two factors will be functions of the coordinates, its total value for any (x,y,z) coordinate in equilibrium is a constant(the three dimensional generalization is trivial). In other words we have
\[V_\text{ec}=V(x)+\text{k}T\cdot\text{ln(c(x))}\]
- with V(x) = e · U(x) = electrostatic potential energy.
- The electrochemical potential thus is a real energy like the potential energy or kinetic energy.
Obviously, in equilibrium (which means that nowhere in the material do we have a net current flow) the electrochemical potential must have the same value anywhere in the material.
- This reminds us of the Fermi energy. In fact, the electrochemical potential is nothing but the Fermi energy and the Fermi distribution in disguise.
- However, since we are considering classical particles here, we get the classical approximation to the Fermi distribution which is, of course, the Boltzmann distribution for EF or Vec, respectively, defining the zero point of the energy scale.
This is easy to see: Just rewriting the equation from above for c(x) yields
\[c(x)=\text{exp}-\frac{(Vx)-V_\text{ec}}{\text{k}T}\]
- What we have is the simple Boltzmann distribution for classical particles with the energy (Vx) – Velectrochem.
Calculating the Debye Length
First we realize that the voltage or potential distribution (voltage times e) in the interior of a material in equilibrium can only be caused by concentration distributions of carriers that obey equilibrium statistics, i.e. the Boltzmann or the Fermi distribution.
- This is simply what the equation above tells us.
What we still need in order to calculate the Debye length is a linkage between potentials e ·U(x) = V(x) and concentrations c(x).
- This is of course what the Poisson equation, the main equation for electrostatics, is all about. We will only look at the one-dimensional case here. The Poisson equation than states
\[-\frac{\text{d}^2 U}{\text{d}x^2} = \frac{\text{d}{\color{purple}E}}{\text{d}x} = \frac{\text{e}\cdot c(x)}{\varepsilon\varepsilon_0}\]
- Now, for good conductors (i.e. c(carriers) ≈ density of atoms ≈ 1022 cm–3), only a few of the carriers (a very small percentage) are needed to screen any reasonable electrical field. If you do not see this, do the exercise!
Exercise 2.5.1: Field Screening
Consider a capacitor made of parallel metal plates in air with an area of 1 cm2 at a distance of 1 cm.
- How many electrons per cm2 do you need on the surface to provide for some field E ending there?
- What would be the maximum charge density for reasonable field strengths up to an ultimate limit of about 10 MV/cm? (For higher field strengths you will get violent discharge).
- How does this number compare to the average volume density of electrons in metals. Consider, e.g., from how far away from the surface you have to collect electrons to achieve the required surface density, if you allow the volume density in the afflicted volume to decrease by x %?
Solution 2.5.1: Field Screening
1. How many electrons per cm2 do you need on the surface a capacitor made of parallel metal plates in air with an area of 1 cm2 and distance 1 cm to provide for some field E ending there?
The relation between the field E resulting from a homogeneous two-dimensional charge distribution and the charge density ρarea is
\[E=\frac{Q}{\varepsilon_0 \cdot A} = \frac{\rho_\text{area}}{\varepsilon_0}\]
- with Q = charge in [C], A = area considered, ρarea = areal density of the charge.
- Compare the two formulas for the capacity C of the capacitor formed by the parallel plates if you are not sure about the equation above. We have:
\[C=\frac{\varepsilon_0 \cdot A}{d}=\frac{Q}{U} \,\text{and}\,E=\frac{U}{d}\]
2. What would be the maximum density for reasonable field strengths up to an ultimate limit of about 10 MV/cm? (For higher field strengths you will get violent discharge).
Lets look at some numbers (ε0 = 8,854 · 10–14 C/Vcm)
|
(rather low)
|
(breakdown limit of "normal dielectrics") |
(close to ultimate breakdown limit) |
| ρarea | 8.85 · 10–11 C/cm2 | 8.85 · 10–9 C/cm2 | 8.85 · 10–7 C/cm2 |
3. How does this number compare to the average volume density of electron in metals. Consider, e.g., from how far away from the surface you have to collect electrons to achieve the required surface density, if you allow the volume density in the afflicted volume to decrease by x %?
The average volume density of electrons in metals is about 1 electron/atomic volume.
- Lets keep thing easy and take for the size datom = 1 Å, which gives 1 Å3 = 10–3 nm3 for the volume of one atom. The volume density of atoms or electrons per cm3 is thus ρvolume = 1024 electrons/cm3.
- The areal density is whatever is contained in a volume with an extension of just one atom diameter in one direction, i.e.
\[\rho_\text{areal} = \rho_\text{volume} \cdot d_\text{atom} =10^{-17}\, \text{electrons/cm}^2\]
- If we want to collect a surplus charge of Qsurplus = 8,85 · 10–7 C/cm2, the maximum charge from above, from a volume Vsurplus by reducing the concentration of 10–24 electrons/cm3 by x %, we have
- \[Q_\text{surplus}=\frac{\rho_\text{volume}\cdot d}{100\cdot x}\\ d=\frac{100\cdot x\cdot Q_\text{surplus}}{\rho_\text{volume}} = \frac{x\cdot 8.85 \cdot 10^{-5}}{10^{24}}cm=x\cdot 8.85 \cdot 10^{-29} \text{cm}\]
In words: Whatever value we like for x, we only have to change the volume concentration of the electrons in an extremely thin layer a tiny little bit to produce any areal charge densities needed - in metals, that is!
We may thus assume within a very good approximation that the carrier density at any point is given by the constant volume density c0 of the field free material, plus a rather small space dependent addition c1(x); i.e.
\[c(x)=c_0+c_1(x)\]
- Obviously, only c1(x) is important for Poissons equation.
From Boltzmanns distribution we know that
\[\frac{c(x)}{c_0}=1+\frac{c_1(x)}{c_0}=\text{exp}\left(-\frac{\Delta\text{energy}}{\text{k}T}\right)=\text{exp}\left(-\frac{V(x)}{\text{k}T}\right)\]
- because the difference in energy of a carrier in the field free volume (i.e. where we have c0) is simply the electrostatic energy associated with the electrical field.
- Since we assumed c1 << c0, we may with impunity express the exponential function as a Taylor series of which we only retain the first term, obtaining:
\[1+\frac{c(x)}{c_0}\approx 1+\frac{V(x)}{\text{k}T}\\c_1(x)=c_0\cdot\frac{V(x)}{\text{k}T}\]
This is a simple trick, but important. Feeding the result back into Poissons equation yields:
\[\frac{\text{d}^2[c_1(x)]}{\text{d}x^2}=\frac{\text{e}^2\cdot c_0\cdot c_1(x)}{\varepsilon\cdot \varepsilon_0\cdot\text{k}T}\]
For a simple one-dimensional case with a surface at x = 0 we obtain the final solution
\[c_1(x)=c_1(x=0)\cdot \text{exp}-\frac{x}{d}\]
The quantity d is the Debye length we were after, it is obviously given by
\[d={\color{red}\text{Debye length}}=\left(\frac{\varepsilon\cdot\varepsilon_0\cdot\text{k}T}{\text{e}^2 \cdot c_0}\right)^{1/2}\]
The Debye length is sometimes also called Debye-Hückel length (which is historically correct and just).
- c1(x = 0), of course, is given by the boundary condition, which for our simple case is:
\[c_1(x=0)=c_0\cdot\frac{V(x=0)}{\text{k}T}\]
What is the meaning of the Debye length? Well, generalizing a bit, we look at the general case of a material having some surplus charge at a definite position somewhere in a material
- Consider for example the phase boundary of a (charged) precipitate, a charged grain boundary in some crystal, or simply a (point) charge somehow held at a fixed position somewhere in some material. The treatment would be quite similar to the one-dimensional case given here.
What we know now is quite important:
- If you are some Debye lengths away from these fixed charges, you will not "see" them anymore; their effect on the equilibrium carrier distribution then is vanishingly small.
- The Debye length resulting in any one of these situations thus is nothing but the typical distance needed for screening the surplus charge by the mobile carriers present in the material.
- In other words, after you moved about one Debye length away from the surplus charge, its effects on the mobile charges of the material are no longer felt.
More about the Debye length can be found in the Hyperscript "Semiconductors".

