2.5.3 Nernst's Equation
- Page ID
- 2774
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nernst's equation gives the voltage between two materials in close contact, i.e. the potential difference between the two materials. From the foregoing discussion, we know already two important facts about this potential:
- It will change from one value to the other over a distance across the junction that is given by the (two) Debye lengths of the system.
- The corresponding carrier concentrations are equilibrium concentrations and thus governed by the Boltzmann distribution (considering only classical particles at this point).
If the potential difference is ∆U, we thus, using the Boltzmann distribution, obtain for the concentration of the carriers c1 in material 1, and c2 in material 2:
\[\frac{}{}=\text{exp}-\frac{\text{e}\cdot\Delta U}{\text{k}T}\]
- This is already Nernst's equation (or law) - in a somewhat unusual way of writing.
Usually we (and everybody else) use the Boltzmann distribution to compute concentrations as a function of some other known parameters - the energy in this case. But this is not the only way for using a general equation!
- Like any equation, it also works in in reverse: If we know the concentrations, we can calculate the energy difference that must go with them!
- The important point now is that the concentrations of electrons in metals, but also of ions in ionic conductors, or holes in semiconductors, or any mobile carrier a few Debye lengths away from the junction, are fixed - there is no need to compute them!
- What is not fixed is the potential difference e · ∆U a few Debye lengths away from the junction, and that is what we now can obtain from the above equation by rewriting it for ∆U:
\[\DeltaU=-\frac{\text{k}T}{\text{e}}\cdot \text{ln}\frac{c_1}{c_2}\]
This is Nernst's equation in its usual, but somewhat simplified form. We may briefly consider two complications:
1. If the particles carry z elementary charges, the first factor will now obviously writekT/(z · e).
2. If the interaction between particles is not negligible (which would mean, e.g., that Ficks law in its simple form would not be usable), the concentrations have to be replaced by the activities a of the particles. If you want to know in detail what activities are - use the link. But all you have to know at this point is that activities are the particle concentrations corrected for interaction effects. To give an example: If a particle concentration is 1019 cm–3, the activity might only be 5 · 1018 cm–3. If you use this factually wrong number, simple equations like the Boltzmann distribution that do not take into account particle interactions can still be used. If the activity numbers are very different from the real concentration numbers, you are no longer doing Materials Science, but chemistry. Using this, we obtain the general version of Nernst's law.
\[\DeltaU=-\frac{\text{k}T}{z\cdot\text{e}}\cdot\text{ln}\frac{a_1}{a_2}\]
Nernsts law, being the Boltzmann distribution in disguise, is of course extremely general. It gives the potential difference and thus the voltage of any contact between two materials that have sufficiently large concentrations of mobile carriers so that an equilibrium distribution can develop. It describes, among other things
- The contact voltage (Volta potential) between two metals (i.e.thermocouples).
- The built-in potential in pn-junctions
- The voltage of any battery or accumulator.
- The voltage of fuel cells.
- The voltage produced by certain kinds of sensors.
The last issue merits some brief explanation. Let's assume a material with a sufficiently large concentration of mobile O– ions at interstitial sites (in other word, mobile interstitial point defects) at the working temperature - take Y2O3 stabilized ZrO2 as an example (whatever that may be).
- Use it to measure the amount of oxygen in a given gas mixture with the following oxygen sensor device:
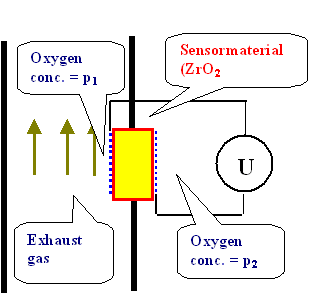
The sensor material experiences two different oxygen concentrations on its two surfaces, one of which is known (oxygen in air, a constant for all practical purposes), the other one is the concentration in the exhaust gas of a car which is supposed to be measured by the voltmeter
- The sensor material experiences two different oxygen concentrations on its two surfaces, one of which is known (oxygen in air, a constant for all practical purposes), the other one is the concentration in the exhaust gas of a car which is supposed to be measured by the voltmeter
In equilibrium, we will have some reaction between the oxygen in the gas and the oxygen in the crystal in the sense that oxygen will either come out, or diffuse into the material.
- What we might expect is that the concentration of interstitial oxygen in the crystal will be larger near to the surface with the large oxygen gas concentration (air) compared to the surface exposed to a lower oxygen concentration (exhaust).
- The gradient in the (negatively charged) oxygen concentration inside the material then will be determined by the Debye length of the system (in the real thing, which is ZrO2, it will be just a few nm).
- In total, the concentration [O]S of mobile O-interstitials right at the surface will be somehow tied to the partial pressure pO of the oxygen on both sides; lets say we have a general relation like
\[[O]_S=\left(\text{const.}\cdot p_O\right)^n\]
- But any other (reasonable) relation you can think of will be just as good.
Nernst's law then tells us immediately, how the voltage between the two electrodes depends on the oxygen concentration or partial pressure in the exhaust: For the assumed relation we have
\[\begin{align} \Delta U &= -\frac{\text{k}T}{\text{e}} \cdot \text{ln} \frac{c_1}{c_2} \\ \Delta U &= -\frac{\text{k}T}{\text{e}} \cdot \text{ln} \frac{(p_1)^n}{(p_2)^n} \\ \Delta U &= -\frac{\text{k}T}{\text{e}} \cdot \text{ln} \frac{p_1}{p_2} \end{align}\]
- This is quite remarkable: We have an equation for the voltage that develops across some sensor as a function of the difference of the oxygen concentration on two sides of the sensor without knowing much about the details of the sensor! All we have to assume is that there is some mobile O–, no other free carriers, and that establishing equilibrium does not take forever.
- Only if you want to know the precise value of n do you have to delve into the detailed reactions at the interfaces.
This is essentially the working principle of not only the oxygen sensor in the exhaust system of any modern car ("λ - Sonde"), but of most, if not all, solid state sensors.

