3.4.6: Plotting MOS I-V

Now we use two of the equations (3.5.6 and 3.5.10) that we found in the discussion about MOS Regimes to calculate a set of \(V_{\text{d sat}}\) and \(I_{\text{d sat}}\) values for various value of \(V_{\text{gs}}\). (Note that \(V_{\text{gs}}\) must be greater than \(V_{t}\) for the two equations to be valid.) When we get the numbers, we build a little table.

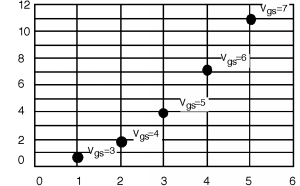
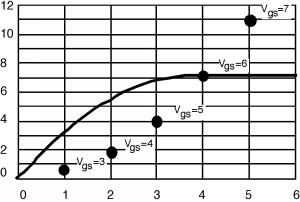
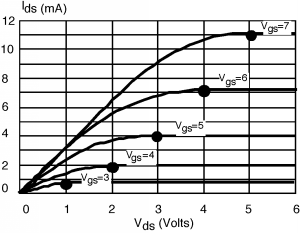
Once we have the numbers (Table \(\PageIndex{1}\), then we sketch a piece of graph paper with the proper scale, and plot the points on it. Once the \(\left(I_{\text{d sat}}, \ V_{\text{d sat}}\right)\) points have been determined, it is easy to sketch in the \(I\text{-}V\) behavior. You just draw a curve from the origin up to any given point, having it "peak out" just at the dot, and then draw a straight line at \(I_{\text{d sat}}\) to finish things off. One such curve is shown in Figure \(\PageIndex{2}\). And then finally in Figure \(\PageIndex{3}\) they are all sketched in. Your curves probably won't be exactly right but they will be good enough for a lot of applications.

Table \(\PageIndex{1}\): Results of calculating \(V_{\text{d sat}}\) and \(I_{\text{d sat}}\)

\(V_{\text{gs}}\)	\(V_{\text{d sat}} \ (\mathrm{V})\)	\(I_{\text{d sat}} \ (\mathrm{mA})\)
\(3\)	\(1\)	\(0.44\)
\(4\)	\(2\)	\(1.76\)
\(5\)	\(3\)	\(3.96\)
\(6\)	\(4\)	\(7.04\)
\(7\)	\(5\)	\(11\)

Figure \(\PageIndex{1}\): Plotting \(I_{\text{d sat}}\) and \(V_{\text{d sat}}\).

Figure \(\PageIndex{2}\): Sketching in one of the \(I\text{-}V\) curves.

Figure \(\PageIndex{3}\): The complete set of curves.

There is a particularly easy way to measure by \(k\) and \(V_{t}\) for a MOSFET. Let's first introduce the schematic symbol for the MOSFET; it looks like Figure \(\PageIndex{4}\). Let's take a MOSFET and hook it up as shown in Figure \(\PageIndex{5}\).

Figure \(\PageIndex{4}\): Schematic symbol for a MOSFET

Figure \(\PageIndex{5}\): Circuit for finding \(V_{t}\) and \(k\)

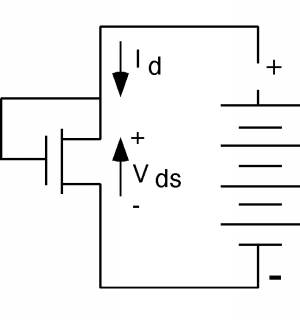
Since the gate of this transistor is connected to the drain, there is no doubt that \(V_{\text{gs}} - V_{\text{ds}}\) is less than \(V_{t}\). In fact, since \(V_{\text{gs}} = V_{\text{ds}}\), their difference is zero. Thus, for any value of \(V_{\text{ds}}\), this transistor is operating in its saturated condition. Since \(V_{\text{gs}} = V_{\text{ds}}\), we can rewrite a previous equation derived equation from the section on MOS regimes as \[I_{d} = \frac{k}{2} \left(V_{\text{ds}} - V_{t}\right)^{2}\]

Now let's take the square root of both sides: \[\sqrt{I_{d}} = \sqrt{\frac{k}{2}} \left(V_{\text{ds}} - V_{t}\right)\]

So if we make a plot of \(\sqrt{I_{d}}\) as a function of \(V_{\text{ds}}\), we should get a straight line, with a slope of \(\sqrt{\frac{k}{2}}\) and an \(x\)-intercept of \(V_{t}\).

Figure \(\PageIndex{6}\): Obtaining \(V_{t}\) and \(k\)

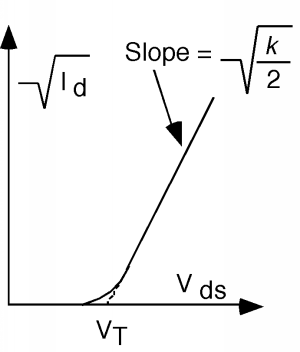
Because of the expected non-ideality, the curve does not go all the way to \(V_{t}\), but deviates a bit near the bottom. A simple linear extrapolation of the straight part of the plot however, yields an unambiguous value for the threshold voltage \(V_{t}\).