3.2.1: Airfoil Nomenclature
- Page ID
- 78103
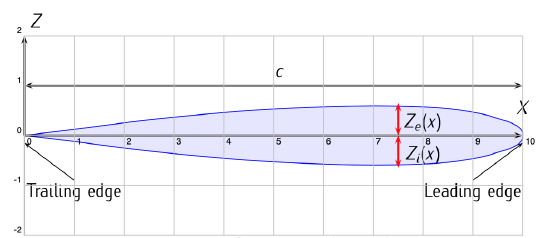
Figure 3.10: Description of an airfoil.
The main parts of an aerodynamic airfoil are: the chord, \(c\), which is the segment joining the leading edge of the airfoil, \(x_{le}\), and the trailing edge, \(x_{te}\). To describe the airfoil, one only needs to know the functions \(z_e (x)\) and \(z_i (x)\), the extrados and the intrados of the airfoil, respectively. See Figure 3.10.
Another form of describing airfoils is to consider them as the result of two different contributors:
- \(C(x)\), representing the camber of the airfoil:
\[C(x) = \dfrac{z_e (x) + z_i (x)}{2}.\label{eq3.2.1.1}\] - \(E(x)\), which gives the thickness of the airfoil:
\[E(x) = z_e (x) - z_i (x).\label{eq3.2.1.2}\]
According to Equation (\(\ref{eq3.2.1.1}\)) and Equation (\(\ref{eq3.2.1.2}\)), it yields:
\[z_e (x) = C(x) + \dfrac{1}{2} E(x).\]
\[z_i (x) = C(x) - \dfrac{1}{2} E(x).\]
A symmetric airfoil is that in which \(C(x) = 0 \forall x\).
The thickness of the airfoil is the maximum of \(E(x)\). The relative thickness of the airfoil is the quotient between thickness and camber, and it is usually expressed in percentage.
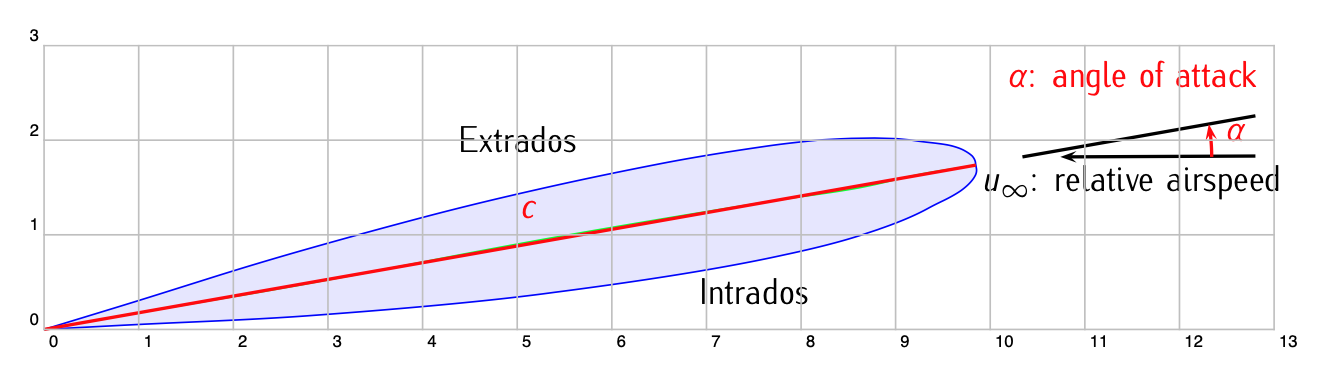
Figure 3.11: Description of an airfoil with angle of attack.
The angle of attack \(\alpha\) is the angle formed by the direction of the velocity (\(u_{\infty}\)) of the air current with no perturbation, that is, sufficiently far away, with a reference line in the airfoil, typically the chord line. See Figure 3.11. Therefore, to give an angle of attack to the airfoil it is only necessary to rotate it around an arbitrary point \(x_0\). In the hypothesis of a low relative thickness (\(\le\) 15 - 18%), a mathematical approximation of this rotation is obtained adding to both \(z_e (x)\) and \(z_i (x)\) the straight line \(z = (x_0 - x) \alpha\), so that it yields:
\[z_e (x) = C(x) + \dfrac{1}{2} E(x) + (x_0 - x) \alpha.\]
\[z_i (x) = C(x) - \dfrac{1}{2} E(x) + (x_0 - x) \alpha.\]
This breaking down analysis into different contributors will be very useful in the future to analyze the contributors of an airfoil to aerodynamic lift: camber, thickness, and angle of attack.


