3.2.2: Generation of aerodynamic forces
- Page ID
- 78104
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
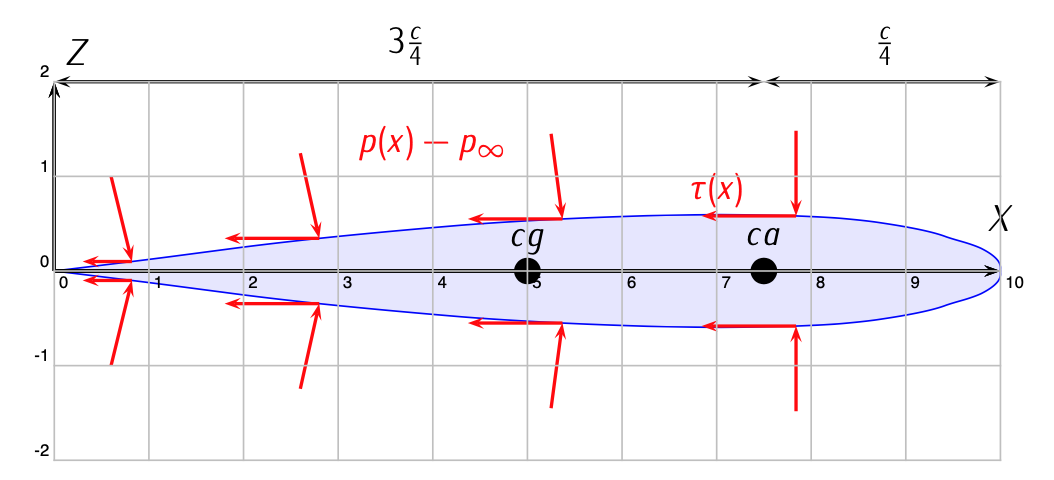
Figure 3.12: Pressure and friction stress over an airfoil.
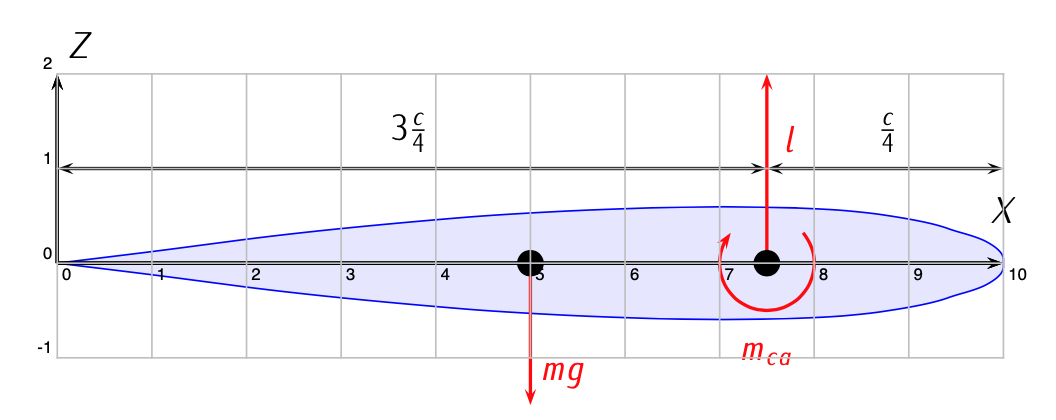
Figure 3.13: Aerodynamic forces and torques over an airfoil.
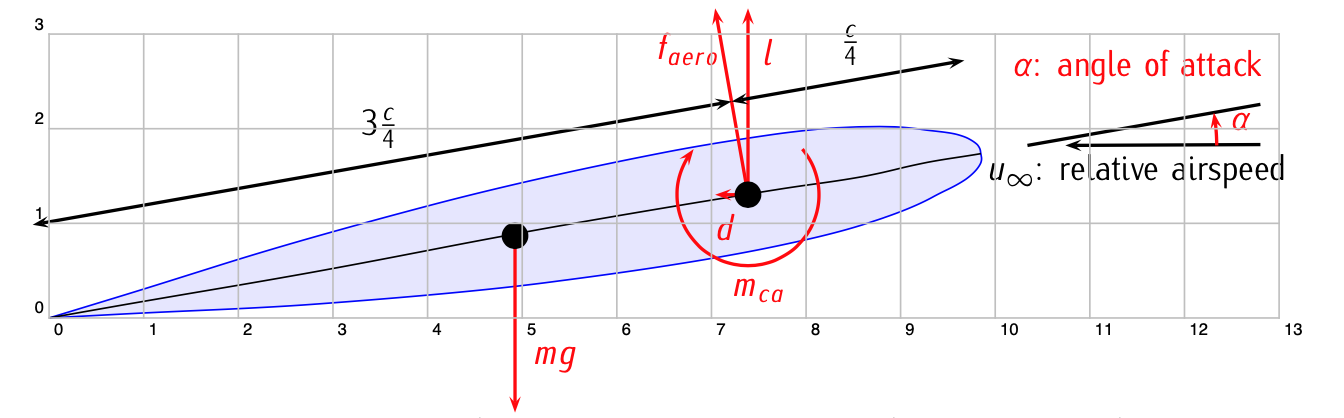
Figure 3.14: Aerodynamic forces and torques over an airfoil with angle of attack.
The actions of the air over a body which moves with respect to it give rise, at each point of the body’s surface, to a shear stress tangent to the surface due to viscosity and a perpendicular stress due to the pressure. Thus, a pressure distribution and a shear stress distribution are obtained over the surface of the body.
Integrating the distribution over the surface of the body, one obtains the aerodynamic forces:
\[f_{aero} = \int (p(x) - p_{\infty}) \cdot dx + \int \tau (x) \cdot dx.\]
Taking the resultant of the distribution and multiplying by the distance to a fixed point (typically the aerodynamic center, located approximately at \(c/4\)), one obtains the aerodynamic torques:
\[m_{ca} = \int (p(x) - p_{\infty}) (x - x_{c/4}) \cdot dx + \int \tau (x - x_{c/4}) \cdot dx.\]
Figure 3.12 , Figure 3.13, and Figure 3.14 illustrate it.
The lift in an airfoil comes, basically, from the pressure forces. The drag in an airfoil
comes from both the friction forces (shear stress) and the pressure forces.
Regarding drag forces, it is important to remember the already mentioned about the boundary layer. The thicker the boundary layer is, the greater the drag due to pressure effects is. In particular, when the flow drops off along the airfoil and becomes turbulent (boundary layer transition), the drag due to pressure effects increases dramatically. Furthermore, friction forces exist, which are greater in turbulent flow rather than in laminar flow. Typically, the contribution to drag of friction forces is lower than the contribution of pressure forces. Therefore, a smart design of an airfoil regarding the behavior of the boundary layer is key to minimize drag forces.
The lift forces are due to the camber, the angle of attack, and the thickness of the airfoil, which conform an airfoil shape so that the pressures in the extrados are lower that pressures in the intrados. The generation of lift can be summarized as follows:
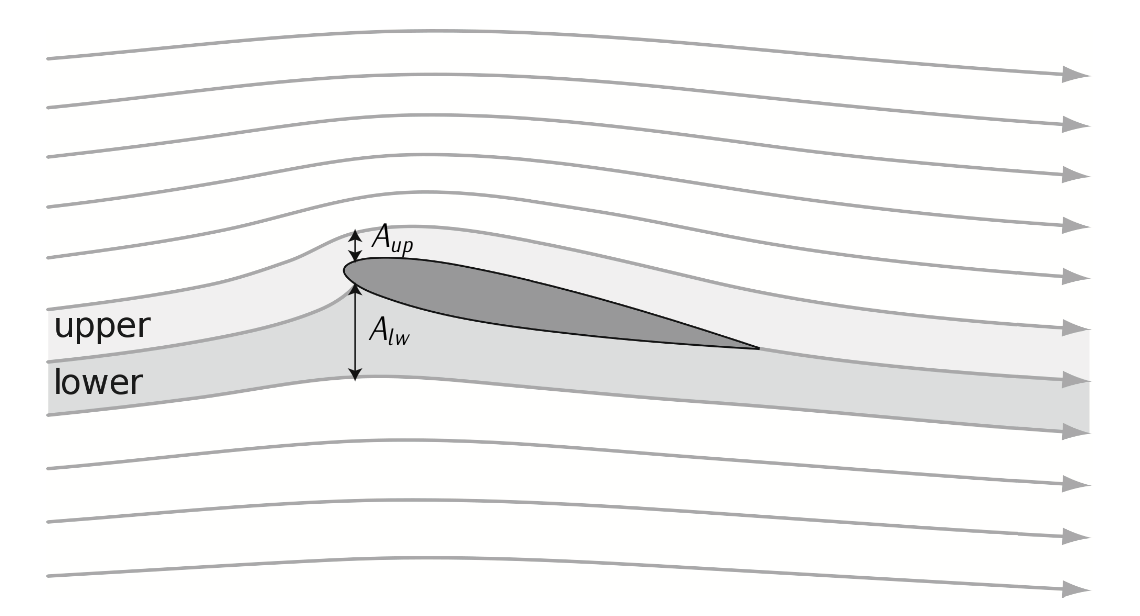
Figure 3.15: Lift generation. Modified from Wikimedia Commons / Public Domain.
- Because of the law of mass continuity (Equation (3.1.2.1)) the flow velocity increases over the top surface of the airfoil more than it does over the bottom surface. This is illustrated in Figure 3.15.
-
As a consequence of Bernoulli effect3 (Equation (3.1.3.5)), the pressure over the top surface of the airfoil is less than the pressure over the bottom surface.
-
Because of the lower pressure over the top surface of the airfoil is less than the pressure over the bottom surface, the airfoil experiences a lift force upwards.
Therefore, this simplified statement of the equations of fluid mechanics give a qualitative idea of the aerodynamic forces. However, the resolution of the equations of fluid mechanics (Navier-Stokes equations) is extremely difficult, even though counting with the most powerful numerical tools. From the theoretical point of view they are studied using simplifications. From the experimental point of view, it is common practice to test scale-models in wind tunnels. The wind tunnels is an experimental equipment able to produce a controlled air flow into a testing chamber.
3. For an incompressible flow, from Bernoulli Equation (3.1.3.5), where the velocity increases, the static pressure decreases.


