3.2.4: Compressibility and drag-divergence Mach number
- Page ID
- 78106
Given an airfoil with a specific angle of attack, if the speed of flight increases, the velocities of the air flow over the airfoil also increase. In that case, the coefficient of pressures increases and also the coefficient of lift does so. For Mach number close to \(M = 1\), \(c_p\) and \(c_l\) can be approximated by the Prandtl-Glauert transformation:
\[c_p = \dfrac{c_{p, inc}}{\sqrt{1 - M^2}};\]
\[c_l = \dfrac{c_{l, inc}}{\sqrt{1 - M^2}};\]
where subindex \(inc\) refers to the value of the coefficient in incompressible flow.
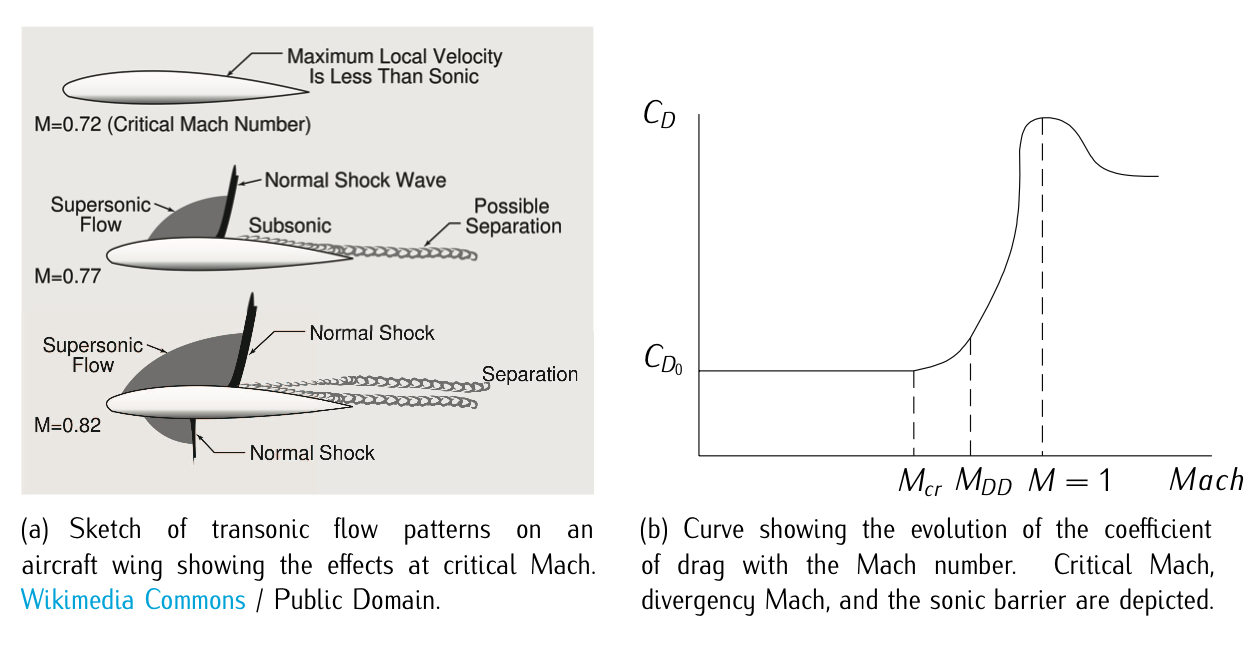
Figure 3.18: Divergence Mach.
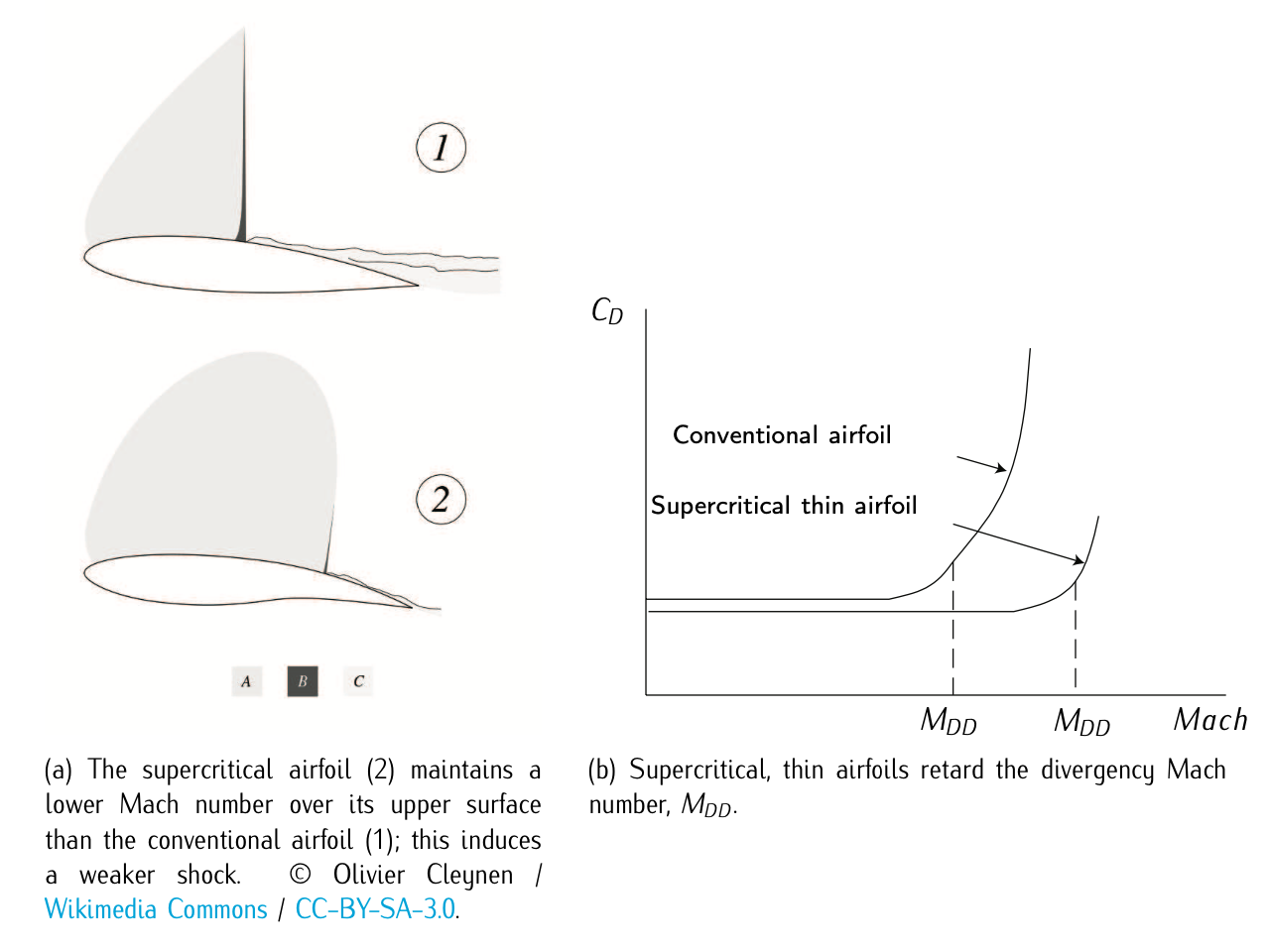
Figure 3.19: Supercritical airfoils.
On the other hand, the coefficient of drag remains practically constant until the airplane reaches the so called critic velocity, a subsonic velocity for which a point of extrados reaches the sonic velocity. It appears a supersonic region and waves shocks are created, giving rise to an important increase of drag. This phenomena is referred to as drag divergence.
The velocity at which this phenomena appears is refereed to as drag divergence Mach number, \(M_{DD}\). Commercial aircraft can not typically overpass this velocity. There is not a unique definition on how to calculate this velocity. Two of the most used conditions are:
\[\dfrac{\partial c_d}{\partial M} = 0.1; \text{ and }\]
\[\Delta c_d = 0.002.\]
Airlines seek to fly faster if the consumption does not raise too much. For that reason, it is interesting to increase \(M_{DD}\). In transonic regimes, airfoils can be designed with thin relative thickness. Another design is the so-called supercritical airfoils, whose shape permits reducing the intensity of the shock wave. In supersonic regimes, it appears another contributor to drag, the wave drag. Supersonic airfoils are designed very thin with very sharp leading edges.


