7.1.6: Performances in gliding
- Page ID
- 78152
In all generality, a glider is an aircraft with no thrust. In stationary linear motion in vertical plane, the equations are as follows:
\[D = mg \sin \gamma,\]
\[L = mg \cos \gamma,\]
and dividing:
\[\tan \gamma_d = \dfrac{D}{L} = \dfrac{C_D}{C_L} = \dfrac{1}{E(\alpha)},\]
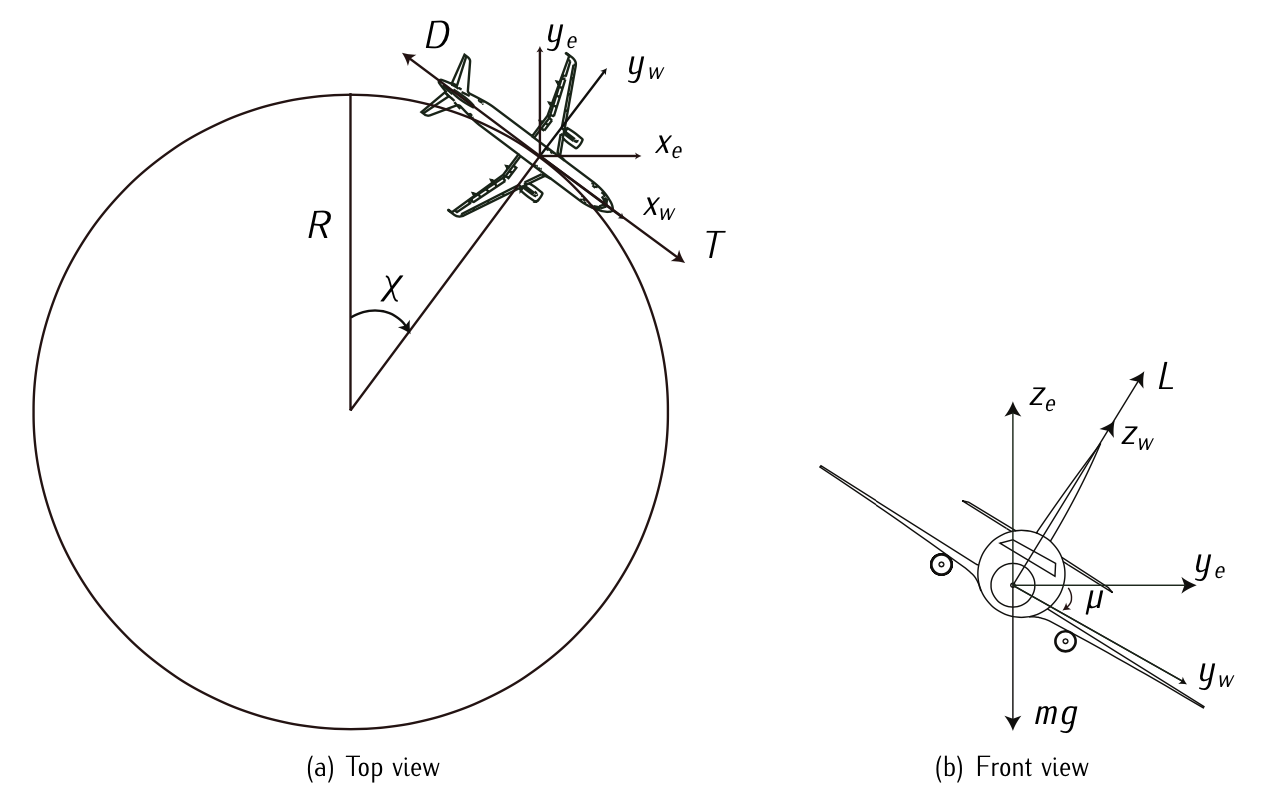
Figure 7.3: Aircraft forces in a horizontal loop.
where \(\gamma_d\) is the descent path angle \((\gamma_d = -\gamma)\). As in stationary linear-horizontal flight, in order to increase the velocity of a glider it is necessary to reduce the angle of attack. Moreover, the minimum gliding path angle will be obtained flying with the maximum aerodynamic efficiency. The descent velocity of a glider \((V_d)\) can be defined as the loss of altitude with time, that is:
\[V_d = V\sin \gamma_d \cong V \gamma_d.\]


