7.1.7: Performances in turn maneuvers
- Page ID
- 78153
Horizontal stationary turn
Consider the additional hypotheses:
- Consider a symmetric flight in the horizontal plane.
- There is no wind.
- The mass and the velocity of the aircraft are constant.
The 3DOF equations governing the motion of the airplane are:
\[T = D,\label{eq7.1.7.1}\]
\[m V \dot{\chi} = L \sin \mu ,\label{eq7.1.7.2}\]
\[L \cos \mu = mg,\label{eq7.1.7.3}\]
\[\dot{x}_e = V \cos \chi, \label{eq7.1.7.4}\]
\[\dot{y}_e = V \sin \chi.\label{eq7.1.7.5}\]
In a uniform (stationary) circular movement, it is well known that the tangential velocity is equal to the angular velocity (\(\dot{\chi}\)) multiplied by the radius of turn \((R)\):
\[V = \dot{\chi} R.\]
Therefore, System (\(ref{eq7.1.7.1}\), \(ref{eq7.1.7.2}\), \(ref{eq7.1.7.3}\), \(ref{eq7.1.7.4}\), \(ref{eq7.1.7.5}\)) can be rewritten as:
\[T = \dfrac{1}{2} \rho SC_{D_0} + \dfrac{2kn^2 (mg)^2}{\rho V^2 S},\]
\[n \sin \mu = \dfrac{V^2}{gR},\]
\[n = \dfrac{1}{\cos \mu} \to n > 1,\]
\[\dot{x}_e = V \cos \chi,\]
\[\dot{y}_e = V \sin \chi.\]
where \(n = \dfrac{L}{mg}\) is the load factor. Notice that the load factor and the bank angle are \(mg\) inversely proportional, that is, if one increases the other reduces and vice versa, until the bank angle reaches \(90^{\circ}\), where the load factor is infinity.
The stall speed in horizontal turn is defined as:
\[V_S = \sqrt{\dfrac{2mg}{\rho S C_{L_{\max}}} \dfrac{1}{\cos \mu}}\]
Ideal looping
The ideal looping is a circumference of radius R into a vertical plane performed at constant velocity. Consider then the following additional hypotheses:
- Consider a symmetric flight in the vertical plane.
- \(\chi\) can be considered constant.
- The aircraft performs a leveled wing flight, i.e., \(\mu = 0\).
- There is no wind.
- The mass and the velocity of the aircraft are constant.
The 3DOF equations governing the motion of the airplane are:
\[T = D + mg \sin \gamma,\]
\[L = mg \cos \gamma + mV \dot{\gamma},\]
\[\dot{x}_e = V \cos \gamma,\]
\[\dot{h}_e = V \sin \gamma,\]
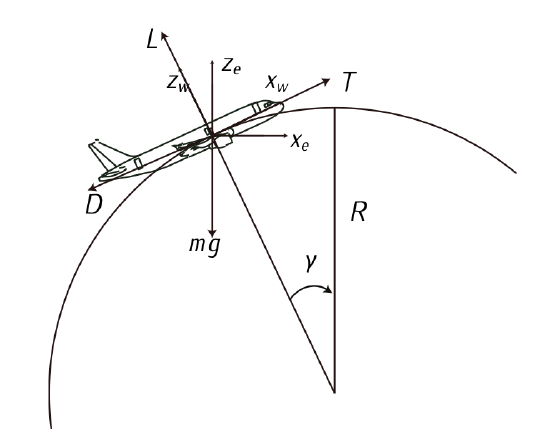
Figure 7.4: Aircraft forces in a vertical loop.
In a uniform (stationary) circular movement, it is well known that the tangential velocity is equal to the angular velocity (\(\dot{\gamma}\) in this case) multiplied by the radius of turn (\(R\)):
\[V = \dot{\gamma} R.\]
The load factor and the coefficient of lift in this case are:
\[n = \cos \gamma + \dfrac{V^2}{gR},\]
\[C_L = \dfrac{2mg}{\rho V^2 S} (\cos \gamma + \dfrac{V^2}{gR}).\]
Notice that the load factor vaires in a sinusoidal way along the loop, reaching a maximum value at the superior point (\(n_{\max} = 1 + \tfrac{V^2}{gR})\) and a minimum value at the inferior point (\(n_{\min} = \tfrac{V^2}{gR} - 1\)).


