4.6.1.1: Stability of Body with Shifting Mass Centroid
- Page ID
- 688

Fig. 4.44. The effects of liquid movement on the \(\overline{GM}\).
Ships and other floating bodies carry liquid or have a load which changes the mass location during tilting of the floating body. For example, a ship that carries wheat grains where the cargo is not properly secured to the ship. The movement of the load (grains, furniture, and/or liquid) does not occur in the same speed as the body itself or the displaced outside liquid. Sometimes, the slow reaction of the load, for stability analysis, is enough to be ignored. Exact analysis requires taking into account these shifting mass speeds. However, here, the extreme case where the load reacts in the same speed as the tilting of the ship/floating body is examined. For practical purposes, it is used as a limit for the stability analysis. There are situations where the real case approaches to this extreme. These situations involve liquid with a low viscosity (like water, alcohol) and ship with low natural frequency (later on the frequency of the ships). Moreover, in this analysis, the dynamics are ignored and only the statics is examined (see Figure 4.44). A body is loaded with liquid ``B'' and is floating in a liquid ``A'' as shown in Figure 4.44. When the body is given a tilting position the body displaces the liquid on the outside. At the same time, the liquid inside is changing its mass centroid. The moment created by the inside displaced liquid is \[M_{in} = g\rho_{lB}\beta I_{xxB}\] Note that \(I_{xxB}\) isn't the same as the moment of inertia of the outside liquid interface. The change in the mass centroid of the liquid ``A'' then is \[\overline{G_{1}G'_{1}} = \frac{\not{g} \not{\rho_{lB}}\beta I_{xxB}}{\not{g}V_{B}\not{\rho_{lB}}} = \frac{I_{xxB}}{V_{B}}\] Equation 50 shows that \(\overline{GG'}\) is only a function of the geometry. This quantity, \(\overline{G_{1}G'_{1}}\), is similar for all liquid tanks on the floating body. The total change of the vessel is then calculated similarly to center area calculations. \[\not{g}m_{total}\overline{GG'} = \rightarrow{gm_{body}} + \not{g} m_{f} \overline{G_{1}G'_{1}}\] For more than one tank, it can be written as \[\overline{GG'} = \frac{g}{W_{total}}\sum_{i=1}^{n} \overline{G_{i}G_{i}}\rho_{li}V_{i} = \frac{g}{W_{total}} \sum_{i=1}{n}\frac{I_{xxbi}}{V_{bi}}\] A new point can be defined as \(G_{c}\). This point is the intersection of the center line with the vertical line from \(G'\). \[\overline{GG_{c}} = \frac{\overline{GG'}}{sin\beta}\] The distance that was used before \(\overline{GM}\) is replaced by the criterion for stability by \(\overline{G_{c}M}\) and is expressed as \[\overline{G_{c}M} = \frac{g\rho_{A}I_{xxA}}{\rho_{s}V_{body}} - \overline{BG} - \frac{1}{m_{total}}\frac{I_{xxb}}{V_{b}}\] If there are more than one tank partially filled with liquid, the general formula is \[\overline{G_{c}M} = \frac{g\rho_{A}I_{xxA}}{\rho_{s}V_{body}} - \overline{BG} - \frac{1}{m_{total}}\sum_{i=1}^{n}\frac{I_{xxbi}}{V_{bi}}\]
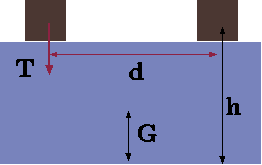
Fig. 4.45. Measurement of GM of floating body.
One way to reduce the effect of the moving mass center due to liquid is done by substituting a single tank with several tanks. The moment of inertial of the combine two tanks is smaller than the moment of inertial of a single tank. Increasing the number of tanks reduces the moment of inertia. The engineer could design the tanks in such a way that the moment of inertia is operationally changed. This control of the stability, \(\overline{GM}\), can be achieved by having some tanks spanning across the entire body with tanks spanning on parts of the body. Movement of the liquid (mostly the fuel and water) provides way to control the stability, \(GM\), of the ship.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


