6.8: Yagi et al. (1972)
- Page ID
- 30852
6.11.1 Introduction
Yagi et al. (1972) carried out experiments with sands and gravels in pipes with diameters of 0.087 m, 0.1003 m and 0.1552 m and spatial concentrations up to 40%. In the 0.087 m diameter pipe they used particles with diameters of 0.75 mm and 8.0 mm. In the 0.1003 m diameter pipe they used particles with diameters of 0.25 mm, 0.65 mm, 1.28 mm and 7.0 mm. In the 0.1552 m diameter pipe they used particles with diameters of 0.91 mm, 8.75 mm, 27.5 mm and 45 mm. The ratios of the larger particles to the pipe diameters is very large, up to about 30%. The wide range of particle diameters and particle diameter to pipe diameter ratios and the fact that they measured both the spatial volumetric concentration and the delivered volumetric concentration, makes these experiments very valuable, although almost forgotten in public literature. For the correlation of pressure losses and physical and operational parameters, they use the \(\ \phi\) and ψ according to Durand & Condolios (1952).
\[\ \phi=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v t}}}\]
\[\ \Psi=\frac{\mathrm{v}_{\mathrm{ls}}^{2} \cdot \sqrt{\mathrm{C}_{\mathrm{x}}}}{\mathrm{g} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{D}_{\mathrm{p}}}=\frac{2}{2} \cdot \frac{\mathrm{v}_{\mathrm{ls}}^{2} \cdot \sqrt{\mathrm{C}_{\mathrm{x}}}}{\mathrm{g} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{D}_{\mathrm{p}}}=2 \cdot \mathrm{F}_{\mathrm{L}}^{2} \cdot \sqrt{\mathrm{C}_{\mathrm{x}}}\]
Remark: Yagi et al. (1972) use the symbol √Cd or √CD, which normally is the square root of the drag coefficient, but according to their paper they use the √Cx of Durand & Condolios (1952), which is the square root of the particle Froude number.
6.11.2 Pressure Losses
Yagi et al. (1972) give different equations for constant transport (delivered) volumetric concentration and constant spatial volumetric concentration. However all equations have the following form:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v t}}}=\Phi=\mathrm{K} \cdot \Psi^{-\alpha}\]
Based on the Durand & Condolios (1952) FL value for large particles of 1.34 and √Cx of 0.84, Yagi et al. (1972) use a value of ψ=3 for the LDV. For very large particles this should be smaller than 3, about 2.22. For the smallest particles used here this should be larger than 3, about 7.5. Based on Durand & Condolios (1952) and others, the value of α is expected to have a value between 1.5 and 2 for heterogeneous flow (spatial concentration), so around and above the LDV. For large particles below the LDV and small particles far below the LDV a value of 1 is expected, based on the sliding bed regime (spatial concentration). For large particles above the LDV a value between 1 and 1.5 is expected based on the sliding flow regime (spatial concentration). For constant delivered volumetric concentration curves, slightly higher values of this power are expected, due to decreasing slip between particles and carrier liquid with increasing line speed. The values found by Yagi et al. (1972) match these trends well, however it should be mentioned that the value of ψ=3 is not always an accurate value to separate the sliding bed regime from the heterogeneous regime, sometimes resulting in slightly higher values than expected.
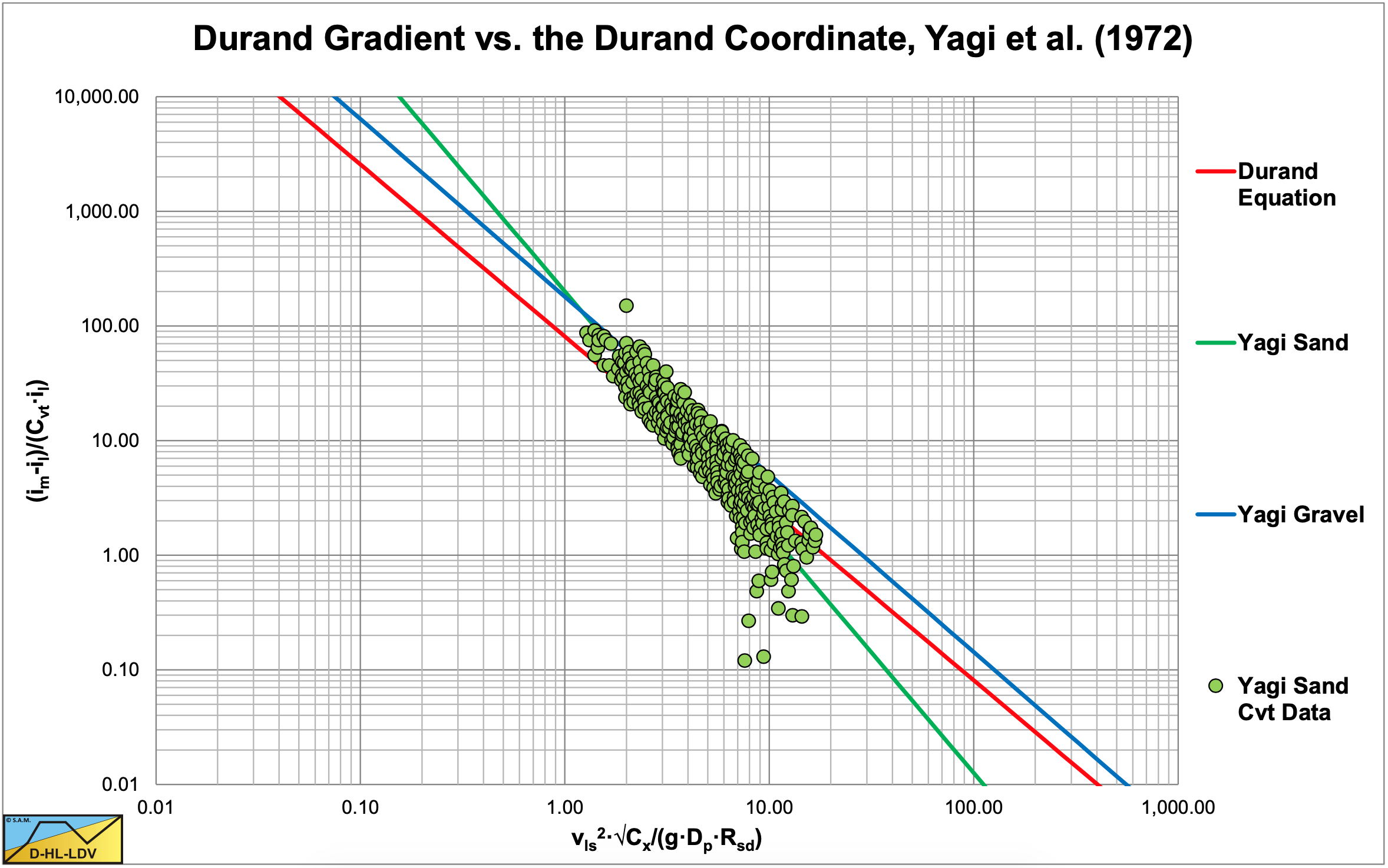
Figure 6.11-1 and Figure 6.11-2 show the data of Yagi et al. (1972) in the \(\ \phi\) and ψ coordinate system for delivered (transport) volumetric concentration. The sand curve is steeper than the Durand & Condolios (1952) curve, while the gravel curve has about the same steepness. The gravel curve however has a larger coefficient and is thus higher. The sand curve crosses the Durand & Condolios (1952) curve at about ψ=4.5, which is close to the LDV of the smaller particles.
In the \(\ \phi\) and ψ coordinate system, an ordinate equal to the Rsd of the solids gives the ELM curve. Now it is known that medium sized particles may have a resistance comparable to the pure liquid resistance, resulting in a sudden drop in Figure 6.11-1. This sudden drop results in a higher value of α for medium sands. Basically what happens is that the heterogeneous flow regime and the pseudo homogeneous flow regime are combined into one equation, one power. The same can happen when the sliding bed regime and the heterogeneous or sliding flow regime are combined into one power. Figure 6.11-5 gives an example of data points in two flow regimes.

6.11.2.1 Sand
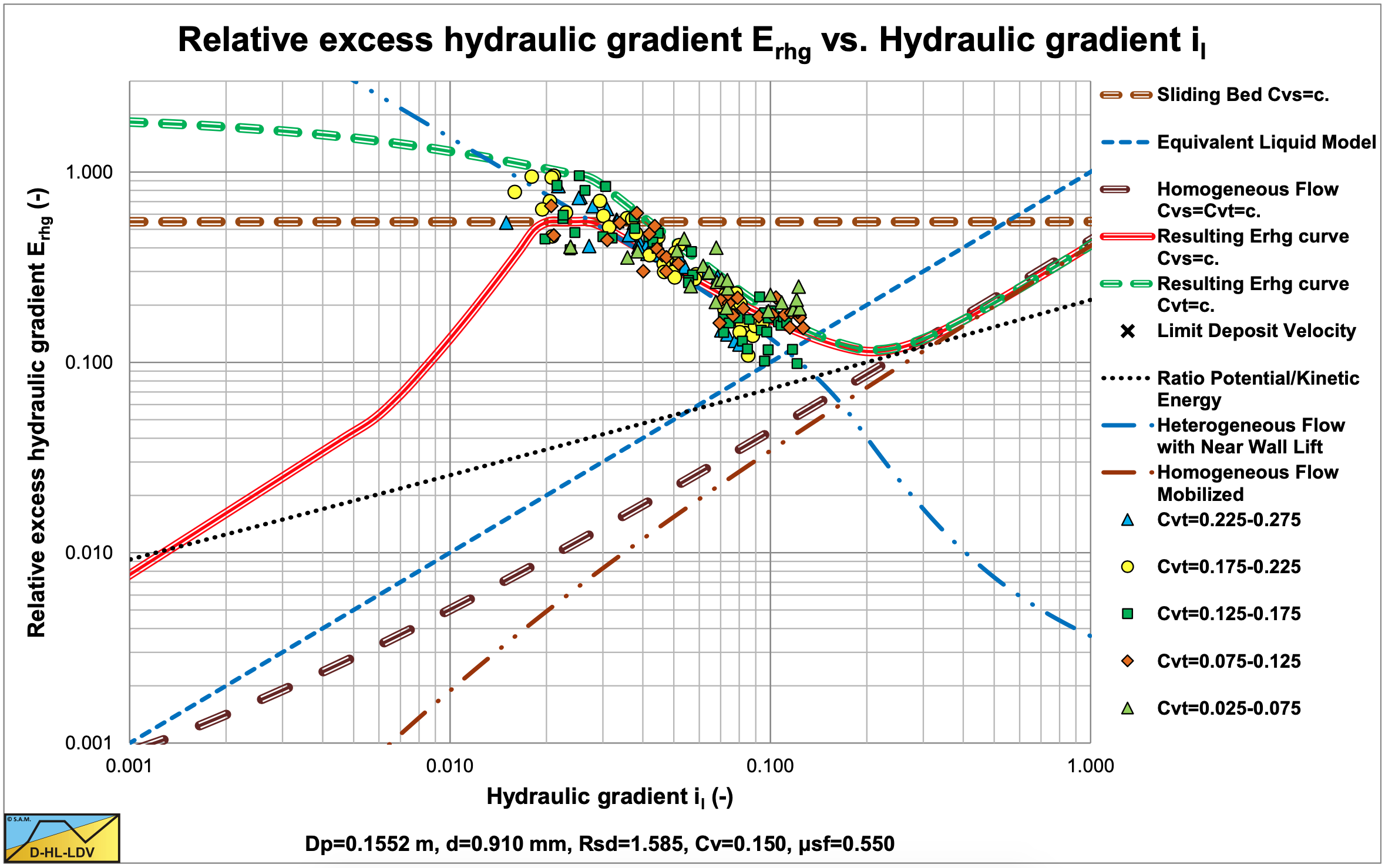
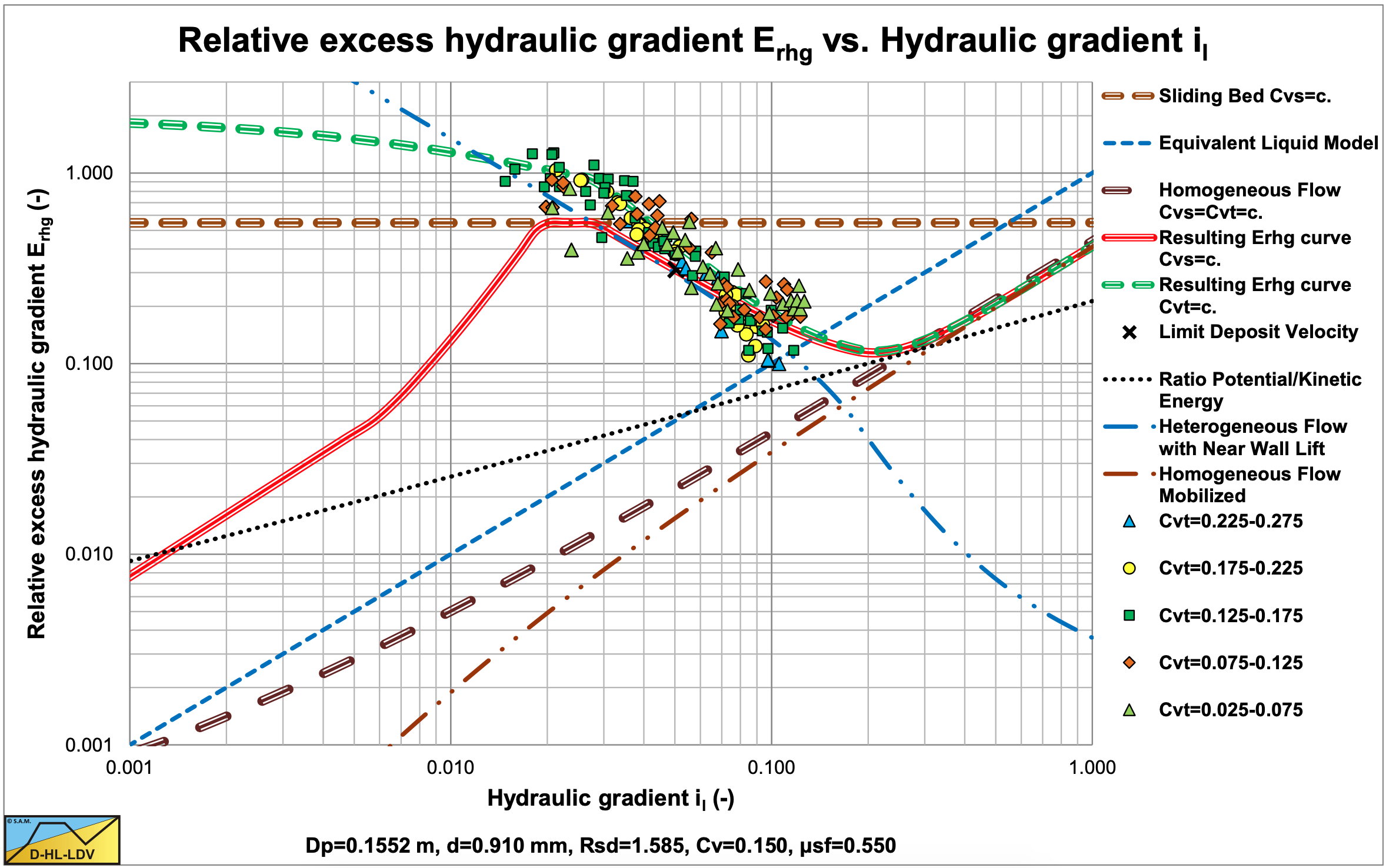
Only detailed data of the 0.91 mm particles in the 0.1552 m diameter pipe are reported for spatial and delivered volumetric concentrations. Figure 6.11-3 and Figure 6.11-4 show these data in a relative excess hydraulic gradient Erhg versus liquid hydraulic gradient il graph.
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}\]
For both cases one cannot distinguish an influence of the concentration. The data points are randomly scattered. The steepness of the delivered concentration data is a bit larger than the steepness of the spatial concentration and the values of the delivered concentration are a bit higher for smaller hydraulic gradient. Near the intersection with the ELM curve (homogeneous flow) the data points are at the same level. One can see in both figures that at the left there is the intersection of the sliding bed regime with the heterogeneous regime, while on the right there is the intersection of the heterogeneous regime with the homogeneous regime. These regime changes will also influence the coefficients found for the equations, which are given below. Above the LDV the powers are equal (α=2.1) which means there is hardly any slip between the particles and the carrier liquid. Below the LDV there is a difference of 0.55 in the power, giving an indication of the slip.
For sand ψ<3 (below LDV), spatial volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}=\phi=\mathrm{K} \cdot \Psi^{-1.55} \quad\text{ with: }\quad \mathrm{K}=\mathrm{1 0 0}\]
For sand ψ>3 (above LDV), spatial volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}=\Phi=\mathrm{K} \cdot \Psi^{-\mathrm{2 . 1}} \quad\text{ with: }\quad \mathrm{K}=\mathrm{1 8 0}\]
For sand, transport volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v t}}}=\Phi=\mathrm{K} \cdot \Psi^{-2.1} \quad\text{ with: }\quad \mathrm{K}=\mathrm{2 0 0}\]
6.11.2.2 Gravel
In the 0.087 m diameter pipe they used particles with a diameter of 8.0 mm. In the 0.1003 m diameter pipe they used particles with a diameters of 7.0 mm. In the 0.1552 m diameter pipe they used particles with diameters of 8.75 mm, 27.5 mm and 45 mm. Only detailed data of the 8.0 mm particles in the 0.087 m diameter pipe are reported for spatial and delivered volumetric concentrations. Figure 6.11-5 and Figure 6.11-6 show these data in a relative excess hydraulic gradient Erhg versus liquid hydraulic gradient il graph. The ratio between the particle diameter and the pipe diameter is about 0.09 which is much larger than the ratio of 0.015-0.018 as mentioned by Wilson et al. (2006) for full stratified flow. Figure 6.11-5 (spatial concentration) shows that the lowest concentrations tend to follow heterogeneous transport, while the higher concentrations tend to follow the sliding bed curve, in between the sliding bed and the heterogeneous curves. One cannot really find an influence of the concentration, as should follow from the Wilson et al. (2006) hydrostatic approach. The data points at lower hydraulic gradients concentrate around Erhg=0.8, which is the sliding friction coefficient, but it is rather high. Figure 6.11-6 shows higher Erhg values resulting from slip. At a certain delivered concentration, the spatial concentration is always higher, resulting in a higher Erhg value. The smaller the liquid hydraulic gradient, the higher the slip and the bigger the difference.
For gravel ψ<3 (below LDV), spatial volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}=\Phi=\mathrm{K} \cdot \Psi^{-\mathrm{1 . 1 6}} \quad\text{ with: }\quad \mathrm{K}=\mathrm{9 8}\]
For gravel ψ>3 (above LDV), spatial volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}=\Phi=\mathrm{K} \cdot \Psi^{-\mathrm{1 . 4 6}} \quad\text{ with: }\quad \mathrm{K}=\mathrm{138}\]
For gravel, transport volumetric concentration:
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v t}}}=\Phi=\mathrm{K} \cdot \Psi^{-1.55} \quad\text{ with: }\quad \mathrm{K}=\mathrm{1 8 0}\]
Below the LDV, the powers differ about 0.4, while above the LDV there is still a difference of 0.1.
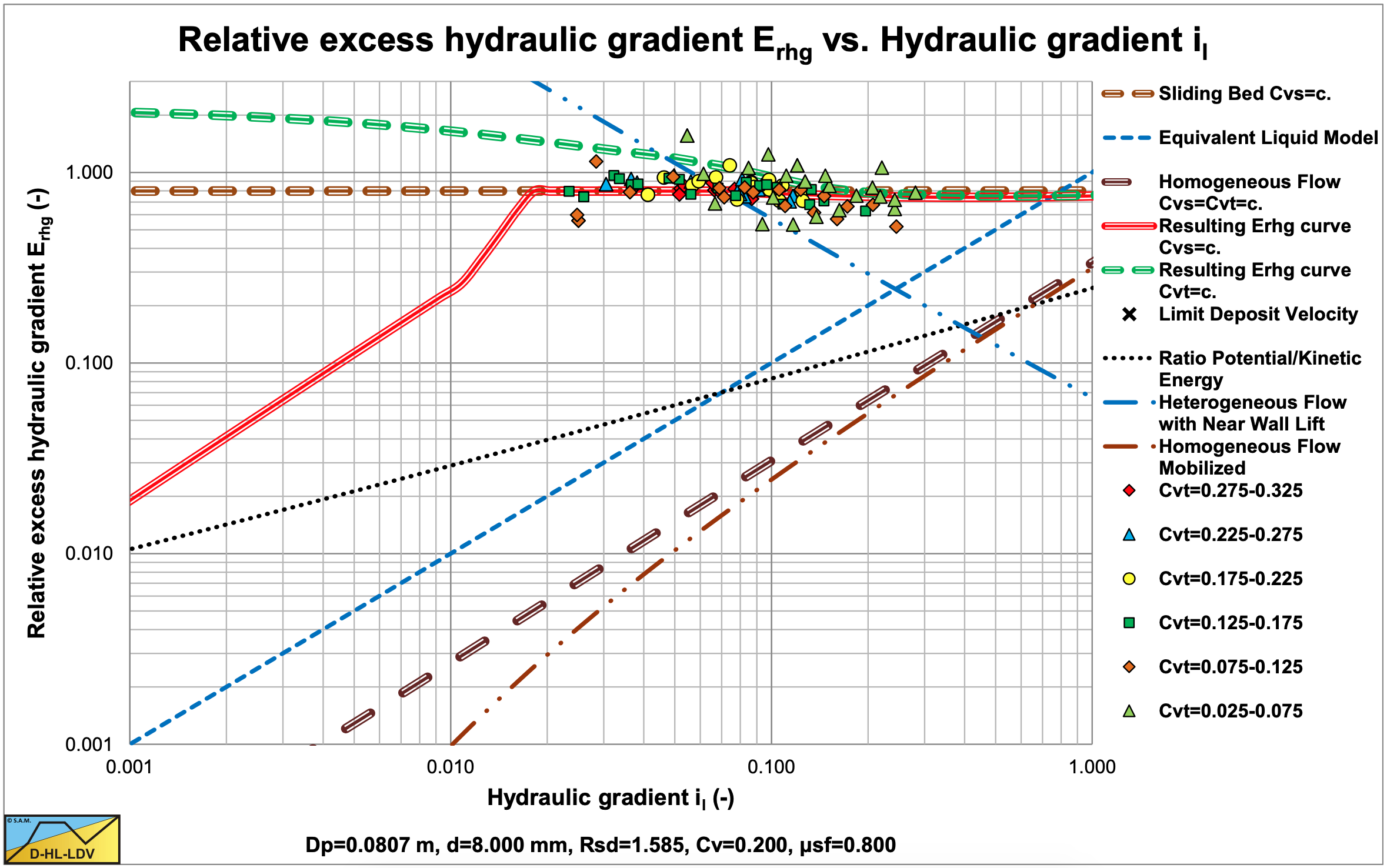
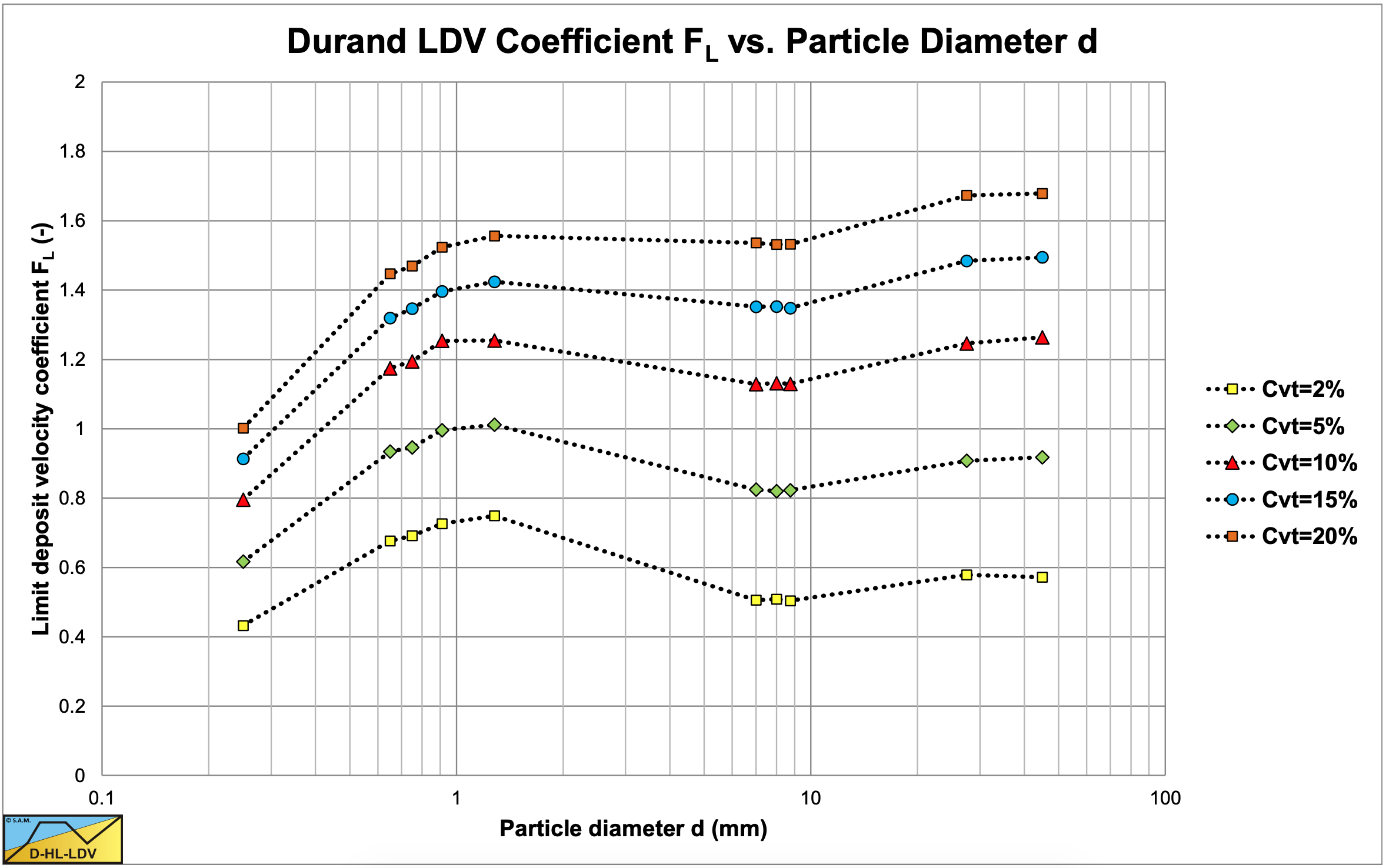
Figure 6.11-7 shows the LDV FL value, as defined by Durand & Condolios (1952) and measured by Yagi et al. (1972).
Yagi et al. (1972) however did not use the criterion that above the LDV no stationary or sliding bed exists, but they used the criterion of the line speed of minimum hydraulic gradient. For concentrations of about 20%, the line speed of minimum hydraulic gradient matches the LDV closely. However for smaller concentrations this minimum criterion results in much smaller FL values than the ones occurring from the real LDV. This can easily be proven by adding the solids contribution to the carrier liquid hydraulic gradient for a range of concentrations, starting at 1%. The result of this is that only the data points of the 20% concentration can be used to determine the FL value at the LDV.
A second complication is the particle size to pipe diameter ratio. According to Wilson et al. (2006), above a certain ratio there will always be a stratified flow resulting in a sort of bed transport. They use a ratio of 0.015-0.018. Large particles cannot be carried by turbulent eddies anymore because they are too large and the result is a sliding bed or sliding flow, high density flow over the bottom of the pipe. Durand & Condolios (1952) did not do experiments in this range and concluded that the FL value increases with increasing particle diameter to a maximum at a particle diameter of about 0.5 mm, after which it decreases slightly to an asymptotic value of about 1.34 for larger particles (base on the Durand (1953) graph). Here an increase is observed for very large particles. Maybe this is because of the large particle diameter to pipe diameter ratio.
It is also a question whether the LDV still has a meaning in the sliding flow regime, because the definition of the LDV states; the line speed above which there is no stationary or sliding bed. But in the case of high density flow over the bottom of the pipe, how to determine whether it is still a sliding bed with decreasing density with increasing line speed or a high density heterogeneous flow?
Still, also for very large particles an equivalent LDV has to be determined, since i twill be used later to determine the slip. This makes the observations of Yagi et al. (1972) very valuable.
6.11.4 The Slip Velocity
Yagi et al. (1972) derived an equation for the slip velocity vsl, based on some theoretical considerations and an empirical relation based on experiments. Particles move slower than the cross sectional averaged line speed, while the liquid moves a bit faster, assuming that the line speed equals the average volume flow divided by the total cross section of the pipe. The average velocity of the particles vp can be derived from the average line speed vls, the volumetric transport concentration Cvt and the volumetric spatial concentration Cvs, according to:
\[\ \mathrm{v}_{\mathrm{p}}=\mathrm{v}_{\mathrm{s}}=\mathrm{v}_{\mathrm{l s}} \cdot \frac{\mathrm{C}_{\mathrm{v t}}}{\mathrm{C}_{\mathrm{v s}}} \quad \Rightarrow \quad \frac{\mathrm{v}_{\mathrm{p}}}{\mathrm{v}_{\mathrm{l s}}}=\frac{\mathrm{C}_{\mathrm{vt}}}{\mathrm{C}_{\mathrm{v s}}}\]
The average line speed is the weighted average of the velocity of the volume fraction of liquid and the volume fraction of the solids (particles), according to:
\[\ \mathrm{v}_{\mathrm{l s}}=\mathrm{v}_{\mathrm{l}} \cdot\left(\mathrm{1}-\mathrm{C}_{\mathrm{v s}}\right)+\mathrm{v}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \quad \Rightarrow \quad \mathrm{v}_{\mathrm{l s}}=\mathrm{v}_{\mathrm{l}} \cdot\left(\mathrm{1}-\mathrm{C}_{\mathrm{v s}}\right)+\mathrm{v}_{\mathrm{l s}} \cdot \mathrm{C}_{\mathrm{v t}}\]
Based on this equation, the average liquid velocity can be derived, which is a bit higher than the average line speed.
\[\ \frac{\mathrm{v}_{\mathrm{l}}}{\mathrm{v}_{\mathrm{ls}}}=\frac{\left(\mathrm{1}-\mathrm{C}_{\mathrm{v t}}\right)}{\left(1-\mathrm{C}_{\mathrm{v s}}\right)}\]
The slip velocity vsl is the difference between the liquid velocity vl and the particle (solids) velocity vp, giving:
\[\ \xi=\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{l s}}}=\frac{\mathrm{v}_{\mathrm{l}}}{\mathrm{v}_{\mathrm{l s}}}-\frac{\mathrm{v}_{\mathrm{p}}}{\mathrm{v}_{\mathrm{l s}}}=\frac{\left(\mathrm{1}-\mathrm{C}_{\mathrm{v t}}\right)}{\left(\mathrm{1 - C}_{\mathrm{v s}}\right)}-\frac{\mathrm{C}_{\mathrm{v} \mathrm{t}}}{\mathrm{C}_{\mathrm{v} \mathrm{s}}}\]
The slip ratio ξ is unknown, but Yagi et al. (1972) found an empirical equation based on many experiments for both sands and gravels:
\[\ \xi=1.3 \cdot \Psi^{-1.4} \quad\text{ with: }\quad \Psi=\frac{\mathrm{v}_{\mathrm{ls}}^{2}}{\mathrm{g} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{D}_{\mathrm{p}}} \cdot \sqrt{\mathrm{C}_{\mathrm{D}}}\]
Once the slip ratio ξ is known, relations for the volumetric spatial concentration Cvs as a function of the volumetric transport concentration Cvt on one hand and for the volumetric transport concentration Cvt as a function of the volumetric spatial concentration Cvs on the other hand can be derived.
\[\ \mathrm{C}_{\mathrm{vs}}=\frac{\mathrm{1}}{2} \cdot\left(\left(\mathrm{1}-\frac{\mathrm{1}}{\xi}\right)+\sqrt{\left(\mathrm{1}-\frac{\mathrm{1}}{\xi}\right)^{2}+\frac{\mathrm{4} \cdot \mathrm{C}_{\mathrm{vt}}}{\xi}}\right)\]
\[\ \mathrm{C}_{\mathrm{v t}}=\mathrm{C}_{\mathrm{v s}}-\xi \cdot\left(\mathrm{C}_{\mathrm{v s}}-\mathrm{C}_{\mathrm{v s}}^{2}\right)\]
The validity of this approach completely depends on the correctness of the slip ratio ξ equation (6.11-15). Since this equation has been derived from the experiments of Yagi et al. (1972) the validity should be limited to pipes with diameters of Dp=0.08 m up to Dp=0.155 m and particles with a diameter d=0.25 mm up to d=45 mm. It should be noted that there was a lot of scatter in the experimental values of the slip ratio.
Yagi et al. (1972) did not distinguish between different flow regimes, where it is clear from their experiments that at low line speeds there was a sliding or fixed bed regime, while at higher line speeds there was a heterogeneous regime. So the slip ratio ξ equation (6.11-15) is an overall fit function. Analyzing the data of Yagi et al. (1972) shows that there is some curvature in the data points as is shown in Figure 6.11-8.
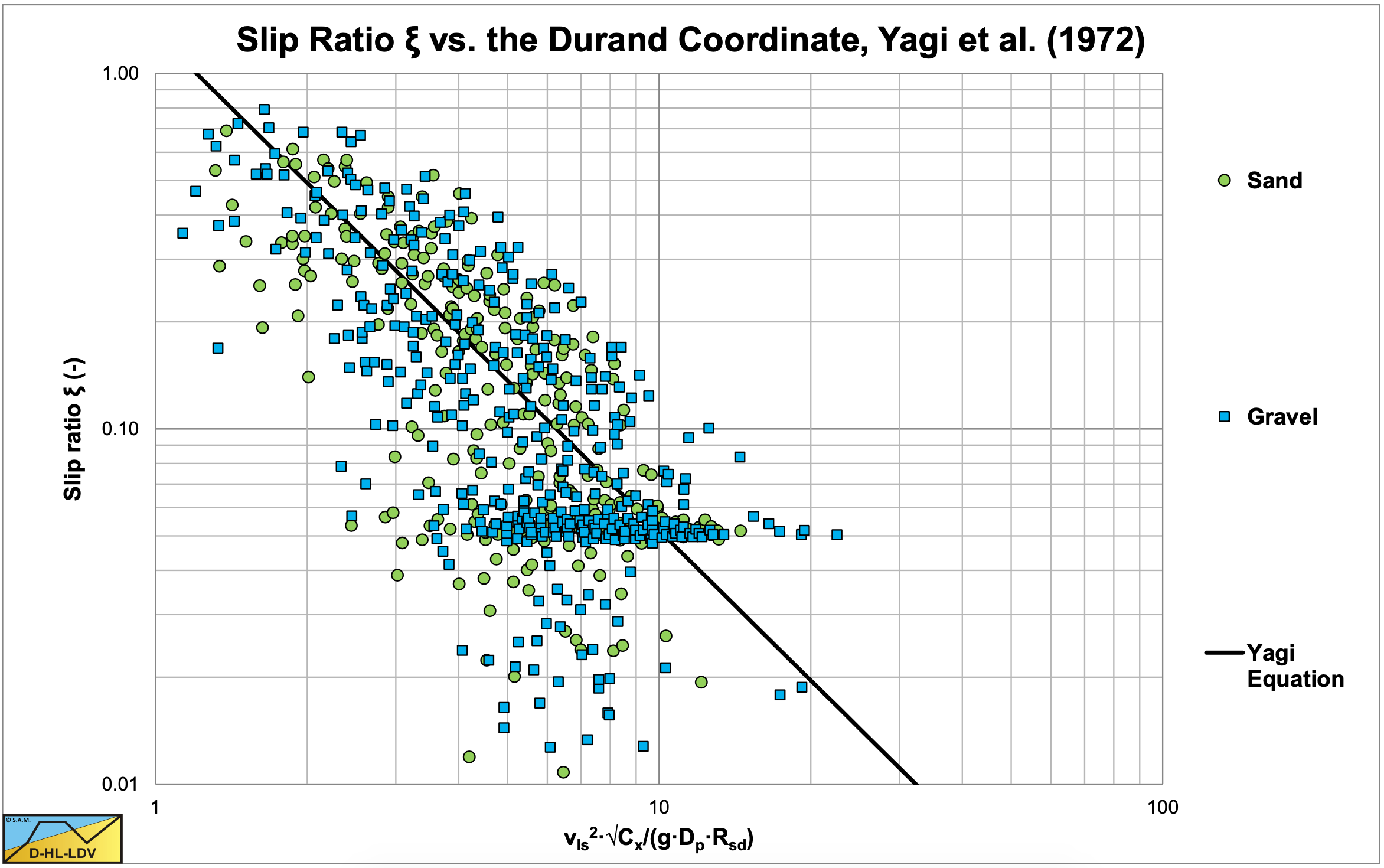
This curvature results from the fact that there were 2 regimes, the sliding or fixed bed regime and the heterogeneous regime. In other words, at low line speeds the regime was below the Limit Deposit Velocity and at higher line speeds the regime was above the Limit Deposit Velocity. According to Durand & Condolios (1952) the Limit Deposit Velocity of large particles will occur at about ψ=2.22 for gravel. For sands it may occur at ψ=3-10. Since most of the experiments of Yagi et al. (1972) were carried out in gravel and coarse sand, a ψ=3 is a reasonable transition between the two regimes.
Although the fit equation improves the prediction of the slip velocity to line speed ratio ξ, the enormous scatter as is shown in Figure 6.11-8 can only lead to the conclusion that there is something else governing the slip velocity to line speed ratio ξ. The main problem of many researchers is that they choose ψ as their dimensionless number with a fixed ratio between the different parameters. Since ψ is dominated by the line speed vls and this line speed is supposed to be reversely proportional to the 3rd power in the relative excess head loss equation, the following equation was proposed by Durand & Condolios (1952):
\[\ \frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{i}_{\mathrm{l}} \cdot \mathrm{C}_{\mathrm{v t}}}=\Phi=\mathrm{K} \cdot \Psi^{-3 / 2} \quad\text{ with: }\quad \mathrm{K}=\mathrm{8 5}\]
This gives a power of 3/2 to the term g . Rsd . Dp and a power of -3/2 to the term \(\ \sqrt{\mathrm{C}_{\mathrm{x}}}\). This is the result of the choice of choosing Froude numbers. Maybe the behavior of the excess head losses does not just follow the flow Froude number Frfl and the particle Froude number Frp, but (also) other dimensionless numbers. Note again that Yagi used the drag coefficient and not the particle Froude number.
At small values of the abscissa in Figure 6.11-8, the slip ratio seems to have a maximum value, although the fit curve would give values close to 1 or even exceeding 1. A value higher than 1 is physically impossible, because that means particles are moving in the opposite direction compared to the line speed. The maximum value is 1 for a stationary bed. However it is more likely that a sliding bed will occur at low line speeds and constant delivered concentration.
It should also be mentioned that often the slip velocity is related to the line speed and not to the liquid velocity. For small concentrations there is not much difference between the line speed and the liquid velocity, but for higher concentrations and a high slip ratio there is. So evaluating data one has to consider which definition is used for the slip velocity.


