3: Bernoulli Equation

The Bernoulli Equation is presented to most all engineering students and even high school students in a simplified form. This allows the development of a basic understanding of fundamental relationships between velocity and pressure within a flow field. It is typically written in the following form:

\[\frac{P}{\rho }+\frac{V^2}{2}+gz=constant\label{3.1} \]

The restrictions placed on the application of this equation are rather limiting, but still this form of the equation is very powerful and can be applied to a large number of applications. But since it is so restrictive care must be take in its application. The restrictions can be stated as:

• incompressible flow (density is constant)
• viscous forces are assumed to be negligible (no internal fluid friction)
• steady flow (no time dependence)
• flow is along a streamline (apply between two points on the same streamline)

The first condition usually means it can be applied to a liquid or to a gas that has a relatively low velocity such that large changes in pressure do not occur. The second condition is a bit vague at best but assumes other forces, such as caused by pressure changes or body forces are much larger than frictional forces which may be valid when the viscosity is low, and/or when spatial velocity derivatives are not too large. The third term is self explanatory and disallows local acceleration. The last term requires the identification of a streamline and that the evaluation of Equation \ref{3.1} occurs between two points along the streamline. A streamline by definition, and as is stated in Chapter 2, assures that the velocity vector is tangent to the streamline. The Bernoulli equation can also be expressed by saying that the constant in the equation is the same at the starting and ending point such that the three terms sum to the same value at these two points and as such can be set equal to each other. Most students reading this will have a fairly extensive use of Equation \ref{3.1} and there are many examples that can be found on the internet. The derivation of this equation is also available in many introductory fluid mechanics textbooks. The basic relationship stems from applying the momentum equation (without viscous forces included) along a streamline. This derivation will not be repeated here.

We wish to develop a more general form of the Bernoulli Equation that eliminates the restrictions to incompressible, steady flow along a streamline. The only restriction then is that viscous forces are ignored. The starting point for this development is the differential Euler’s Equation for the motion of a fluid element that relates the acceleration to the forces caused by pressure and gravity. This can be expressed using the material derivative from Chapter 2 as a balance of acceleration with pressure and body forces per unit mass of fluid:

\[\frac{D\boldsymbol{V}}{dt}=-\frac{1}{\rho }\frac{\partial P}{\partial \boldsymbol{x}}+\boldsymbol{g}\label{3.2} \]

Or in tensor notation as:

\[\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial P}{\partial x_i}+g_i\label{3.3} \]

The pressure term is representative of the net force caused by the compressive load of pressure along the direction of the vector component of interest, on a per mass basis. The body force term is again given as the “\({i}\)” vector component of the gravitational vector. The acceleration terms on the left can be recast using the vector identity for the convective acceleration given in Chapter 2.

\[u_j\frac{\partial u_i}{\partial x_j}=\frac{1}{2}\frac{\partial \left(u_ju_j\right)}{\partial x_j}-{\varepsilon }_{ijk}\left(u_j{\varepsilon }_{klm}\frac{\partial u_m}{\partial x_l}\right)\label{3.4} \]

The last term introduces the vorticity into the equation since the vorticity is defined as the curl of the velocity vector:

\[{\omega }_k={\varepsilon }_{klm}\frac{\partial u_m}{\partial x_l}\]

So the last term becomes the cross product of velocity and vorticity, or:

\[{\varepsilon }_{ijk}\left(u_j{\varepsilon }_{klm}\frac{\partial u_m}{\partial x_l}\right)={\varepsilon }_{ijk}u_j{\omega }_k\]

Notice that the result of this operation is a vector in the “\({i}\)” direction, consistent with the other terms in the Euler equation. By introducing the vorticity into the convective acceleration term, this term can now can be considered to have two components. One is half of the gradient of the magnitude of the velocity vector squared (the first term), and the other is the cross product between the velocity vector and vorticity (a vector). This latter term has been identified as the “Lamb vector”, after the applied mathematician, Horace Lamb (1849-1934).

Euler’s equation can now be rewritten as:

\[\frac{\partial u_i}{\partial t}+\frac{1}{2}\frac{\partial \left(u_ju_j\right)}{\partial x_i}-{\varepsilon }_{ijk}u_j{\omega }_k=-\frac{1}{\rho }\frac{\partial P}{\partial x_i}+g_i\label{3.5} \]

Next we write the Lamb vector as a gradient of some unknown function:

\[\frac{\partial \pi }{\partial x_i}={\varepsilon }_{ijk}u_j{\omega }_k\label{3.6} \]

In this expression \({\pi}\) must be a scalar quantity such that its gradient is a vector. This is done for convenience so that we can then integrate each term of our equation along any desired path, with elemental distance \({ds}\). That is we take the projection of each term along \({ds}\) (take the dot product of each term with vector \({ds})\). However, before we do this we make the following modification to the gravitational term such that we can integrate spatially along \({ds}\).

We can write the gravitational term as a “potential” as:

\[g_i=-g\frac{\partial h}{\partial x_i}\label{3.8} \]

where \(“{h}”\) is a scalar and \(g\) is the magnitude acceleration of gravity. The choice of the symbol \(“{h}”\) is because it will have units of length and if gravity is vertically downward then \(“{h}”\) is vertically upward and represents elevation above some arbitrarily chosen datum. Notice that if \(“{i}”\) is horizontal then \(\frac{\partial h}{\partial x_i}\) is the change in elevation over a differential change in the horizontal direction, consequently the value of \(\frac{\partial h}{\partial x_i}\) is zero. If \(“{i}”\) is in the vertical upward direction then \(\frac{\partial h}{\partial x_i}=1\) and \(g_i=-g\). If \(“{i}”\) is at some angle \({\theta}\) to the horizontal, then \(\frac{\partial h}{\partial x_i}={\mathrm{sin}\theta}\).

We are now able to write the integral along \({ds}\) of Euler’s equation. Note that the dot product of each term results in a scalar that defines the magnitude of the change of the term along direction \({ds}\):

\[\int_s{\frac{\partial u_i}{\partial t}}ds_i+\int_s{\frac{1}{2}\frac{\partial \left(u_ju_j\right)}{\partial x_j}}ds_i+\int_s{\frac{\partial \pi }{\partial x_i}}ds_i+\int_s{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i+\int_s{g\frac{\partial h}{\partial x_i}ds_i=f(t)}}\label{3.9} \]

Since the integration is in space there may be a time dependence of each term that is not accounted for which is why the term on the right hand side appears — a general function of time can be added such that if one takes the spatial derivatives this function will vanish. Note that if there is no time dependence then \({f(t)} = 0\), as well as the first term on the left.

Bringing the time derivative outside of the integral in the first term, and performing the integration along the arbitrary line \({ds}\):

\[\frac{\partial}{\partial{t}}\int_s{u_i}ds_i+\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \pi +\int_s{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i+\Delta \left(gh\right)=f(t)}\label{3.10} \]

where \(\Delta\) represents the change of the variable, or expression, along the line \({s}\). As shown we have two integrals that we can not evaluate at this point. The first represents the local acceleration and how it varies along the integration path. The second is the pressure term. Note however if the flow is incompressible, \({\rho }\) is constant, then we can say that:

\[\int _S{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i=\frac{1}{\rho }\int_s{\frac{\partial P}{\partial x_i}ds_i}}=\Delta \frac{P}{\rho }\]

Equation (3.10) excludes frictional or viscous forces, but that is about its only limitation. As such it is a general form of the Bernoulli Equation. But considering incompressible and steady flow the result is:

\[\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \pi +\Delta \frac{P}{\rho }+\Delta \left(gh\right)=0\label{3.11} \]

Consequently, the sum of these four terms which represent changes along any direction \({s}\) is zero, or

\[\frac{\left(u_ju_j\right)}{2}+\pi +\frac{P}{\rho }+\left(gh\right)=constant\label{3.12} \]

To satisfy some curiosity, one would expect that by applying the four conditions listed above for the specialized form of Equation \ref{3.10} will result in Equation \ref{3.1}. If density is constant the pressure integral term becomes 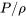. If the flow is steady then the time dependence terms are zero. If the integration is taken along a streamline then we can make the following argument. The velocity vector by definition is aligned with the streamline, therefore the direction of \({ds}\) and \({u{}_{i}}\) are identical. The vorticity may be in any arbitrary direction, but the cross product of \({u{}_{i}}\) and \({\omega_j}\) must be perpendicular to \({ u{}_{i}}\). Consequently, since the integration is for the projection of each term along \({ds}\), and the cross product of \({u{}_{i}}\) and \({\omega_j}\) is normal to \({ds}\) (since it is normal to \({u{}_{i}}\)) then the net effect of this term is zero (has no component along \({ds}\) if \({s }\) is a streamline). So if integration is along a streamline we can delete the Lamb vector effect,\(\Delta \pi =0\). Combining all of these conditions we end up with Eqn (3.1) as we hoped.

Other than along a streamline, another way in which \(\Delta \pi =0\) is if the vorticity is zero along any chosen integration path. That is to say, the vorticity is zero throughout the flow field. Let’s examine the consequences of this condition. If each component of vorticity is zero then we can write a set of conditions, one for each component of the vorticity,

\[{\omega }_i=\left(\frac{\partial u_k}{\partial x_j}-\frac{\partial u_j}{\partial x_k}\right)=0;\mathrm{where}\ i\neq j\neq k\label{3.13} \]

Now we define a “velocity potential” such that

\[u_j=\frac{\partial \phi }{\partial x_j}\label{3.14} \]

This is a rather powerful condition — that a single scalar function,\({\phi}\), can be used to define the velocity field through its partial derivatives. If one takes the derivatives of \({u{}_{k}}\) and \({u{}_{j}}\) as shown in Equation \ref{3.13} but rewrite this in terms of the velocity potential, the result is an identity for \(j\neq k\). That is to say, it is always = 0 since it is possible to reverse the order of differentiation. Therefore it is concluded that if one can replace the velocity vector with the derivatives of the scalar velocity potential defined in Equation \ref{3.14} then the vorticity is zero everywhere. This can also be stated as: a scalar velocity potential exists and can be used to define the velocity field if the flow is vorticity free. Since vorticity can be defined as the degree of local rotation occurring in the flow we say the flow is “irrotational” if the vorticity is zero everywhere.

Using the above definition of a velocity potential, that exists for irrotational flow, it can be said that irrotational flow results in a simplified form of the Bernoulli Equation since \(π\) is zero when the vorticity is zero.

Here we summarize the Bernoulli Equation and how it is modified for different conditions.

1. General form
   \(\int_s{\frac{\partial u_i}{\partial t}}ds_i+\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \pi +\int_s{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i+\Delta \left(gh\right)=f(t)}\)
2. Incompressible flow form
   \(\int_s{\frac{\partial u_i}{\partial t}}ds_i+\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \pi +\Delta \frac{P}{\rho }+\Delta \left(gh\right)=f(t)\)
3. Steady form
   \(\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \pi +\int_s{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i+\Delta \left(gh\right)=0}\)
4. Irrotational, or along a streamline, form
   \(\int_s{\frac{\partial u_i}{\partial t}}ds_i+\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\int_s{\frac{1}{\rho }\frac{\partial P}{\partial x_i}ds_i+\Delta \left(gh\right)=f(t)}\)
5. Combination, steady, incompressible along a streamline, or irrotational
   \(\Delta \left(\frac{\left(u_ju_j\right)}{2}\right)+\Delta \frac{P}{\rho }+\Delta \left(gh\right)=0\)

The last form is that which is most often introduced as a first exposure to the Bernoulli equation, yet it does come with a number of conditions, and one must be reminded that all of the above forms exclude any viscous, or frictional, force effects.

It is important to realize that the Bernoulli equation can be used for rotational or irrotational flow, but the former requires that it be applied along a streamline and viscous forces are not included. The later condition of irrotational flow, also neglects viscous forces but assumes irrotational flow so can be applied between any two points within the flow (not necessarily along a streamline).

In the chapters dealing with irrotational flow we will apply the Bernoulli equation between points where we know information, like far upstream of some object when there is flow over the object, to some point where we would like to calculate information, like on the surface of the object. However, since viscous forces are not included care must be taken to not apply the typical viscous boundary condition, of no-slip (forcing the fluid velocity to be equal to the surface boundary velocity.) Consequently inviscid flows allow slip, which means that the surface velocity of the fluid is some value that may need to be determined. This determination is the subject of the next two chapters.