9.10: Cameras
- Page ID
- 14628
# camerax and cameray are the top left of where the camera view is
camerax = 0
cameray = 0
The camerax and cameray variables track the game coordinates of the "camera". Imagine the game world as an infinite 2D space. This could, of course, never fit on any screen. We can only draw a portion of the infinite 2D space on the screen. We call the area of this portion a camera, because it is as though our screen is just the area of the game world in front what a camera would see. Here’s a picture of the game world (an infinite green field) and the area that the camera can view:
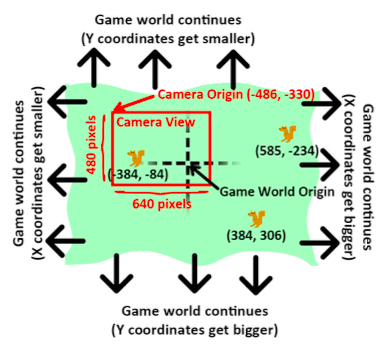
As you can see, the game world XY coordinates keep getting bigger and smaller forever. The game world origin is where the (0, 0) game world coordinates are. You can see that the three squirrels are located (in game world coordinates) at (-384, -84), (384, 306), and (585, -234).
But we can only display 640 x 480 pixel area on the screen (though this can change if we pass different numbers to the pygame.display.set_mode() function), so we need to track where the camera’s origin is located in game world coordinates. In the picture above, the camera is placed at (-486, -330) in game world coordinates.
The picture below shows the same field and squirrels, except everything is given in camera coordinates:
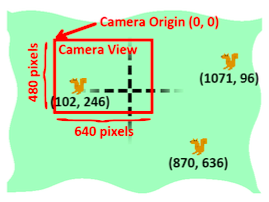
The area that the camera can see (called the camera view) has it’s center (that is, its origin) at the game world coordinates (-486, -330). Since what the camera sees is displayed on the player’s screen, the "camera" coordinates are the same as the "pixel" coordinates. To find out the pixel coordinates of the squirrels (that is, where on the screen they appear), take the game coordinates of the squirrel and subtract the game coordinates of the camera’s origin.
So the squirrel on the left has game world coordinates of (-384, -84) but appears at (102, 246) on the screen in pixel coordinates. (For the X coordinate, -384 - -486 = 102 and for the Y coordinate, -84 - -330 = 246.)
When we do the same calculation to find the pixel coordinates of the other two squirrels, we find that they exist outside of the range of the screen. This is why they don’t appear in the camera’s view.

