1.4: Predicates and Quantifiers
- Page ID
- 6711
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In propositional logic, we can let \(p\) stand for “Roses are red” and \(q\) stand for “Violets are blue.” Then \(p ∧ q\) will stand for “Roses are red and violets are blue.” But we lose a lot in the translation into logic. Since propositional logic only deals with truth values, there’s nothing we can do with \(p\) and \(q\) in propositional logic that has anything to do with roses, violets, or color. To apply logic to such things, we need predicates. The type of logic that uses predicates is called predicate logic, or, when the emphasis is on manipulating and reasoning with predicates, predicate calculus.
A predicate is a kind of incomplete proposition, which becomes a proposition when it is applied to some entity (or, as we’ll see later, to several entities). In the proposition “the rose is red,” the predicate is is red. By it- self, “is red” is not a proposition. Think of it as having an empty slot, that needs to be filled in to make a proposition: “— is red.” In the proposition “the rose is red,” the slot is filled by the entity “the rose,” but it could just as well be filled by other entities: “the barn is red”; “the wine is red”; “the banana is red.” Each of these propositions uses the same predicate, but they are different propositions and they can have different truth values.
If \(P\) is a predicate and a is an entity, then \(P(a)\) stands for the proposition that is formed when \(P\) is applied to \(a\). If \(P\) represents “is red” and \(a\) stands for “the rose,” then \(P(a)\) is “the rose is red.” If \(M\) is the predicate “is mortal” and \(s\) is “Socrates,” then \(M(s)\) is the proposition “Socrates is mortal.”
Now, you might be asking, just what is an entity anyway? I am using the term here to mean some specific, identifiable thing to which a predicate can be applied. Generally, it doesn’t make sense to apply a given predicate to every possible entity, but only to entities in a certain category. For example, it probably doesn’t make sense to apply the predicate “is mortal” to your living room sofa. This predicate only applies to entities in the category of living things, since there is no way something can be mortal unless it is alive. This category is called the domain of discourse for the predicate.\(^9\)
We are now ready for a formal definition of one-place predicates. A one-place predicate, like all the examples we have seen so far, has a single slot which can be filled in with one entity:
Definition 1.6
A one-place predicate associates a proposition with each entity in some collection of entities. This collection is called the domain of discourse for the predicate. If \(P\) is a predicate and a is an entity in the domain of discourse for \(P\), then \(P(a)\) denotes the proposition that is associated with \(a\) by \(P\). We say that \(P(a)\) is the result of applying \(P\) to \(a\).
We can obviously extend this to predicates that can be applied to two or more entities. In the proposition “John loves Mary,” loves is a two-place predicate. Besides John and Mary, it could be applied to other pairs of entities: “John loves Jane,” “Bill loves Mary,” “John loves Bill,” “John loves John.” If \(Q\) is a two-place predicate, then \(Q(a, b)\) denotes the proposition that is obtained when \(Q\) is applied to the entities \(a\) and \(b\). Note that each of the “slots” in a two-place predicate can have its own domain of discourse. For example, if \(Q\) represents the predicate “owns,” then \(Q(a, b)\) will only make sense when \(a\) is a person and \(b\) is an inanimate object. An example of a three-place predicate is “\(a\) gave \(b\) to \(c\),” and a four-place predicate would be “\(a\) bought \(b\) from \(c\) for \(d\) dollars.” But keep in mind that not every predicate has to correspond to an English sentence.
\(^9\) In the language of set theory, which will be introduced in the next chapter, we would say that a domain of discourse is a set, U, and a predicate is a function from U to the set of truth values. The definition should be clear enough without the formal language of set theory, and in fact you should think of this definition—and many others—as motivation for that language.
When predicates are applied to entities, the results are propositions, and all the operators of propositional logic can be applied to these propositions just as they can to any propositions. Let \(R\) be the predicate “is red,” and let \(L\) be the two-place predicate “loves.” If \(a, b, j, m,\) and \(b\) are entities belonging to the appropriate categories, then we can form compound propositions such as:
\(R(a) ∧ R(b)\) \(a\) is red and \(b\) is red
\(¬R(a)\) \(a\) is not red
\(L(j, m) ∧ ¬L(m, j)\) \(j\) loves \(m\), and \(m\) does not love \(j\)
\(L(j,m) → L(b,m)\) if \(j\) loves \(m\) then \(b\) loves \(m\)
\(R(a) ↔ L(j, j)\) \(a\) is red if and only if \(j\) loves \(j\)
Let’s go back to the proposition with which we started this section: “Roses are red.” This sentence is more difficult to handle than it might appear. We still can’t express it properly in logic. The problem is that this proposition is not saying something about some particular entity. It really says that all roses are red (which happens to be a false statement, but that’s what it means). Predicates can only be applied to individual entities.
Many other sentences raise similar difficulties: “All persons are mortal.” “Some roses are red, but no roses are black.” “All math courses are interesting.” “Every prime number greater than two is odd.” Words like all, no, some, and every are called quantifiers. We need to be able to express similar concepts in logic.
Suppose that \(P\) is a predicate, and we want to express the proposition that \(P\) is true when applied to any entity in the domain of discourse. That is, we want to say “for any entity x in the domain of discourse, \(P(x)\) is true.” In predicate logic, we write this in symbols as \(∀x(P(x))\). The \(∀\) symbol, which looks like an upside-down A, is usually read “for all,” so that \(∀x(P(x))\) is read as “for all \(x\), \(P(x)\).” (It is understood that this means for all \(x\) in the domain of discourse for \(P\) .) For example, if \(R\) is the predicate “is red” and the domain of discourse consists of all roses, then \(∀x(R(x))\) expresses the proposition “All roses are red.” Note that the same proposition could be expressed in English as “Every rose is red” or “Any rose is red.”
Now, suppose we want to say that a predicate, \(P\), is true for some entity in its domain of discourse. This is expressed in predicate logic as \(∃x(P(x))\). The \(∃\) symbol, which looks like a backwards E, is usually read “there exists,” but a more exact reading would be “there is at least one.” Thus, \(∃x(P (x))\) is read as “There exists an \(x\) such that \(P(x)\),” and it means “there is at least one \(x\) in the domain of discourse for \(P\) for which \(P(x)\) is true.” If, once again, \(R\) stands for “is red” and the domain of discourse is “roses,” then \(∃x(R(x))\) could be expressed in English as “There is a red rose” or “At least one rose is red” or “Some rose is red.” It might also be expressed as “Some roses are red,” but the plural is a bit misleading since \(∃x(R(x))\) is true even if there is only one red rose. We can now give the formal definitions:
Definition 1.7
Suppose that \(P\) is a one-place predicate. Then \(∀x(P(x))\) is a proposition, which is true if and only if \(P(a)\) is true for every entity \(a\) in the domain of discourse for \(P\) . And \(∃x(P (x))\) is a proposition which is true if and only if there is at least one entity, \(a\), in the domain of discourse for \(P\) for which \(P(a)\) is true. The \(∀\) symbol is called the universal quantifier, and \(∃\) is called the existential quantifier.
The \(x\) in \(∀x(P (x))\) and \(∃x(P (x))\) is a variable. (More precisely, it is an entity variable, since its value can only be an entity.) Note that a plain \(P(x)\)—without the \(∀x\) or \(∃x\)—is not a proposition. \(P(x)\) is neither true nor false because \(x\) is not some particular entity, but just a placeholder in a slot that can be filled in with an entity. \(P(x)\) would stand for something like the statement “\(x\) is red,” which is not really a statement in English at all. But it becomes a statement when the \(x\) is replaced by some particular entity, such as “the rose.” Similarly, \(P(x)\) becomes a proposition if some entity a is substituted for the \(x\), giving \(P(a)\).\(^10\)
An open statement is an expression that contains one or more entity variables, which becomes a proposition when entities are substituted for the variables. (An open statement has open “slots” that need to be filled in.) \(P(x)\) and “\(x\) is red” are examples of open statements that contain one variable. If \(L\) is a two-place predicate and \(x\) and \(y\) are variables, then \(L(x,y)\) is an open statement containing two variables. An example in English would be “\(x\) loves \(y\).” The variables in an open statement are called free variables. An open statement that contains \(x\) as a free variable can be quantified with \(∀x\) or \(∃x\). The variable \(x\) is then said to be bound. For example, \(x\) is free in \(P(x)\) and is bound in \(∀x(P(x))\) and \(∃x(P(x))\). The free variable \(y\) in \(L(x, y)\) becomes bound in \(∀y(L(x, y))\) and in \(∃y(L(x, y))\).
Note that \(∀y(L(x,y))\) is still an open statement, since it contains x as a free variable. Therefore, it is possible to apply the quantifier \(∀x\) or \(∃x\) to \(∀y(L(x,y))\), giving \(\forall x(\forall y(L(x,y))\) and \(\exists x (\forall y (L(x,y)))\). Since all the variables are bound in these expressions, they are propositions. If \(L(x,y)\) represents “\(x\) loves \(y\),” then \(∀y(L(x,y))\) is something like “\(x\) loves everyone,” and \(\exists x(\forall y(L(x, y))\) is the proposition, “There is someone who loves everyone.” Of course, we could also have started with \(∃x(L(x, y))\): “There is someone who loves \(y\).” Applying \(∀y\) to this gives \(\forall y(\exists x(L(x, y))\), which means “For every person, there is someone who loves that person.” Note that \(∀y(L(x,y))\) is still an open statement, since it contains \(x\) as a free variable. Therefore, it is possible to apply the quantifier \(∀x\) or \(∃x\) to \(∀y(L(x,y))\), giving \(∀x(∀y(L(x,y))\) and \(∃x(∀y(L(x,y))\). Since all the variables are bound in these expressions, they are propositions. If \(L(x,y)\) represents “\(x\) loves \(y\),” then \(∀y(L(x,y))\) is something like “\(x\) loves everyone,” and \(\exists x(\forall y(L(x, y))\) is the proposition, “There is someone who loves everyone.” Of course, we could also have started with \(∃x(L(x, y))\): “There is someone who loves \(y\).” Applying \(∀y\) to this gives \(\forall y(\exists x(L(x, y))\), which means “For every person, there is someone who loves that person.” Note in particular that \(\exists x(\forall y(L(x,y))\) and \(\forall y(\exists x(L(x,y))\) do not mean the same thing. Altogether, there are eight different propositions that can be obtained from \(L(x,y)\) by applying quantifiers, with six distinct meanings among them.
\(^{10}\) There is certainly room for confusion about names here. In this discussion, x is a variable and a is an entity. But that’s only because I said so. Any letter could be used in either role, and you have to pay attention to the context to figure out what is going on. Usually, x, y, and z will be variables.
(From now on, I will leave out parentheses when there is no ambiguity. For example, I will write \(∀xP(x)\) instead of \(∀x(P(x))\) and \(∃x∃yL(x,y)\) instead of \(\exists x(\exists y(L(x,y)))\). Furthermore, I will sometimes give predicates and entities names that are complete words instead of just letters, as in \(Red(x)\) and \(Loves(john,mary)\). This might help to make examples more readable.)
In predicate logic, the operators and laws of Boolean algebra still apply. For example, if P and Q are one-place predicates and a is an entity in the domain of discourse, then P (a) → Q(a) is a proposition, and it is logically equivalent to ¬P (a) ∨ Q(a). Furthermore, if x is a variable, then P (x) →Q(x) is an open statement, and ∀x(P (x) → Q(x)) is a proposition. So areP (a) ∧ (∃x Q(x)) and (∀x P (x)) → (∃xP (x)). Obviously, predicate logic can be very expressive. Unfortunately, the translation between predicate logic and English sentences is not always obvious.
Let’s look one more time at the proposition “Roses are red.” If the domain of discourse consists of roses, this translates into predicate logic as \(\forall xRed(x)\). However, the sentence makes more sense if the domain of discourse is larger—for example if it consists of all flowers. Then “Roses are red” has to be read as “All flowers which are roses are red,” or “For any flower, if that flower is a rose, then it is red.” The last form translates directly into logic as \(\forall xRose(x) → Red(x))\). Suppose we want to say that all red roses are pretty. The phrase “red rose” is saying both that the flower is a rose and that it is red, and it must be translated as a conjunction, \(Rose(x) ∧ Red(x)\). So, “All red roses are pretty” can be rendered as \(\forall x(Rose(x) ∧ Red(x)) → Pretty(x)\).
Here are a few more examples of translations from predicate logic to English. Let \(H(x)\) represent “\(x\) is happy,” let \(C(y)\) represent “\(y\) is a computer,” and let \(O(x, y)\) represent “\(x\) owns \(y\).” (The domain of discourse for \(x\) consists of people, and the domain for \(y\) consists of inanimate objects.) Then we have the following translations:
- Jack owns a computer: \(\exists xO(jack, x) ∧ C(x))\). (That is, there is at least one thing such that Jack owns that thing and that thing is a computer.)
- Everything Jack owns is a computer: \(\forall x(O(jack, x) → C(x)\).
- If Jack owns a computer, then he’s happy: \((\exists y(O(jack,y) ∧ C(y))) \to H(jack)\).
- Everyone owns a computer: \(\forall x \exists y (C(y) \top O(x,y))\). (Note that this allows each person to own a different computer. The proposition \(\exists y \forall x (C(y) \top O(x,y))\) would mean that there is a single computer which is owned by everyone.)
- Everyone is happy: \(\forall x H(x)\).
- Everyone is unhappy: \(\forall x(¬H(x))\).
- Someone is unhappy: \(\exists x(¬H(x))\).
- At least two people are happy: \(\exists x \exists y (H(x) \land H(y) \land (x \ne y)\). (The stipulation that \(x \ne y\) is necessary because two different variables can refer to the same entity. The proposition \(\exists x \exists y(H(x) \land H(y)\) is true even if there is only one happy person.)
- There is exactly one happy person: \((\exists x H(x)) \land (\forall y \forall z ((H(y) \land H(z)) \to (y=z)))\). (The first part of this conjunction says that there is at least one happy person. The second part says that if \(y\) and \(z\) are both happy people, then they are actually the same person. That is, it’s not possible to find two different people who are happy.
To calculate in predicate logic, we need a notion of logical equivalence. Clearly, there are pairs of propositions in predicate logic that mean the same thing. Consider the propositions \(¬(\forall xH(x))\) and \(\exists x(¬H(x))\), where \(H(x)\) represents “\(x\) is happy.” The first of these propositions means “Not every- one is happy,” and the second means “Someone is not happy.” These statements have the same truth value: If not everyone is happy, then someone is unhappy and vice versa. But logical equivalence is much stronger than just having the same truth value. In propositional logic, logical equivalence is defined in terms of propositional variables: two compound propositions are logically equivalent if they have the same truth values for all possible truth values of the propositional variables they contain. In predicate logic, two formulas are logically equivalent if they have the same truth value for all possible predicates.
Consider \(¬(\forall xP(x))\) and \(\exists x(¬P(x))\). These formulas make sense for any predicate \(P\), and for any predicate \(P\) they have the same truth value. Unfortunately, we can’t—as we did in propositional logic—just check this fact with a truth table: there are no subpropositions, connected by \(∧, ∨,\) etc, out of which to build a table. So, let’s reason it out: To say \(¬(\forall xP(x))\) is true is just to say that it is not the case that \(P(x)\) is true for all possible entities \(x\). So, there must be some entity a for which \(P(a)\) is false. Since \(P(a)\) is false, \(¬P(a)\) is true. But saying that there is an a for which \(¬P(a)\) is true is just saying that \(\exists x(¬P(x))\) is true. So, the truth of \(¬(\forall xP(x))\) implies the truth of \(\exists x(¬P(x))\). On the other hand, if \(¬(\forall xP(x))\) is false, then \(\forall xP(x)\) is true. Since \(P(x)\) is true for every \(x, ¬P(x)\) is false for every \(x\); that is, there is no entity \(a\) for which the statement \(¬P(a)\) is true. But this just means that the statement \(\exists x(¬P(x))\) is false. In any case, then, the truth values of \(¬(\forall xP(x))\) and \(\exists x(¬P(x))\) are the same. Since this is true for any predicate \(P\), we will say that these two formulas are logically equivalent and write \(¬(\forall xP (x)) ≡ \exists x(¬P (x))\).
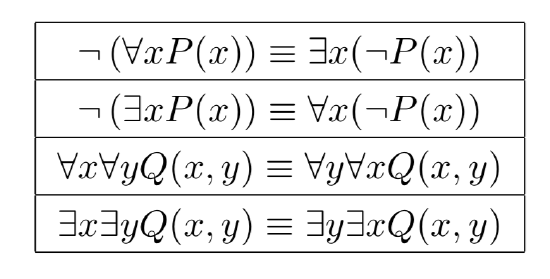
Figure 1.9: Four important rules of predicate logic. P can be any one-place predicate, and Q can be any two-place predicate. The first two rules are called DeMorgan’s Laws for predicate logic.
A similar argument would show that \(¬(\exists xP(x)) ≡ \forall x(¬P(x))\). These two equivalences, which explicate the relation between negation and quantification, are known as DeMorgan’s Laws for predicate logic. (They are closely related to DeMorgan’s Laws for propositional logic; see the exercises.) These laws can be used to help simplify expressions. For example,
\(¬ \forall y(R(y) ∨ Q(y)) ≡ \exists y(¬(R(y) ∨ Q(y)))\)
\(≡ \exists y((¬R(y)) ∧ (¬Q(y))\)
It might not be clear exactly why this qualifies as a “simplification,” but it’s generally considered simpler to have the negation operator applied to basic propositions such as \(R(y)\), rather than to quantified expressions such as \(\forall y(R(y) ∨ Q(y))\). For a more complicated example:
\(¬\exists x(P(x) \land (\forall y(Q(y) \to Q(x)))\)
\(≡ \forall x(\neg(P(x) \land (\forall y (Q(y) \to Q(x))))\)
\(≡ \forall x ((\neg P(x)) \lor (\neg \forall y (Q(y) \to Q(x))))\)
\(≡ \forall x((\neg P(x)) \lor (\exists y(\lor(\lor Q(y) \lor Q(x)))))\)
\(≡ \forall x ((\neg P(x)) \lor (\exists y (\neg \neg Q(y) \lor \neg Q(x))))\)
\(≡ \forall x((\neg P(x)) \lor (\exists y (Q(y) \lor \neg Q(x))))\)
��
DeMorgan’s Laws are listed in Figure 1.9 along with two other laws of predicate logic. The other laws allow you to interchange the order of the variables when two quantifiers of the same type (both \(\exists\) or \(\forall\)) occur together.
To define logical equivalence in predicate logic more formally, we need to talk about formulas that contain predicate variables, that is, variables that act as place-holders for arbitrary predicates in the same way that propositional variables are place-holders for propositions and entity variables are place-holders for entities. With this in mind, we can define logical equivalence and the closely related concept of tautology for predicate logic.
Definition 1.8
Let \(P\) be a formula of predicate logic which contains one or more predicate variables. \(P\) is said to be a tautology if it is true whenever all the predicate variables that it contains are replaced by actual predicates. Two formulas \(P\) and \(Q\) are said to be logically equivalent if \(P ↔ Q\) is a tautology, that is if \(P and Q\) always have the same truth value when the predicate variables they contain are replaced by actual predicates. The notation \(P ≡ Q\) asserts that \(P\) is logically equivalent to \(Q\).
Exercises
1. Simplify each of the following propositions. In your answer, the ¬ operator should be applied only to individual predicates.
a) \(¬ ∀x(¬P (x))\)
b) \(¬ ∃x(P (x) ∧ Q(x))\)
c) \(¬ ∀z(P (z) → Q(z))\)
d) \(\neg ((∀xP (x)) ∧ ∀y(Q(y)))\)
e) \(¬∀x∃yP(x,y)\)
f) \(¬∃x(R(x)∧∀yS(x,y))\)
g) \(¬ ∃y(P (y) ↔ Q(y))\)
h) \(¬(∀x(P (x) → (∃yQ(x, y))))\)
2. Give a careful argument to show that the second of DeMorgan’s laws for predicate calculus, ¬(∀xP (x)) ≡ ∃x(¬P (x)), is valid.
- Find the negation of each of the following propositions. Simplify the result; in your answer, the ¬ operator should be applied only to individual predicates.
a) \(¬∃n(∀sC (s, n))\)
b) \(¬∃n(∀s(L(s, n) → P (s)))\)
c) \(¬∃n(∀s(L(s, n) → (∃x∃y∃zQ(x, y, z)))).\)
d) \(¬∃n(∀s(L(s, n) → (∃x∃y∃z(s = xyz ∧ R(x, y) ∧ T (y) ∧ U (x, y, z)))).\) - Suppose that the domain of discourse for a predicate \(P\) contains only two entities. Show that \(∀xP(x)\) is equivalent to a conjunction of two simple propositions, and \(∃xP(x)\) is equivalent to a disjunction. Show that in this case, DeMorgan’s Laws for propositional logic and DeMorgan’s Laws for predicate logic actually say exactly the same thing. Extend the results to a domain of discourse that contains exactly three entities.
- Let \(H(x)\) stand for “\(x\) is happy,” where the domain of discourse consists of people. Express the proposition “There are exactly three happy people” in predicate logic.
- Let \(T(x,y)\) stand for “\(x\) has taken \(y\),” where the domain of discourse for \(x\) consists of students and the domain of discourse for \(y\) consists of math courses (at your school). Translate each of the following propositions into an unambiguous English sentence:
a) \(∀x∀yT(x,y)\)
b) \(∀x∃yT(x,y)\)
c) \(∀y∃xT(x,y)\)
d) \(∃x∃yT(x,y)\)
e) \(∃x∀yT(x,y)\)
f) \(∃y∀xT(x,y)\) - Let \(F (x, t)\) stand for “You can fool person \(x\) at time \(t\).” Translate the following sentence into predicate logic: “You can fool some of the people all of the time, and you can fool all of the people some of the time, but you can’t fool all of the people all of the time.”
- Translate each of the following sentences into a proposition using predicate logic. Make up any predicates you need. State what each predicate means and what its domain of discourse is.
a) All crows are black.
b) Any white bird is not a crow.
c) Not all politicians are honest.
d) All green elephants have purple feet.
e) There is no one who does not like pizza.
f) Anyone who passes the final exam will pass the course.
g) If x is any positive number, then there is a number y such that \(y2 = x.\) - The sentence “Someone has the answer to every question” is ambiguous. Give two translations of this sentence into predicate logic, and explain the difference in meaning.
- The sentence “Jane is looking for a dog” is ambiguous. One meaning is that there is some particular dog—maybe the one she lost—that Jane is looking for. The other meaning is that Jane is looking for any old dog—maybe because she wants to buy one. Express the first meaning in predicate logic. Explain why the second meaning is not expressed by \(∀x(Dog(x) → LooksFor(jane, x))\). In fact, the second meaning cannot be expressed in predicate logic. Philosophers of language spend a lot of time thinking about things like this. They are especially fond of the sentence “Jane is looking for a unicorn,” which is not ambiguous when applied to the real world. Why is that?


