2.1: Memory
- Page ID
- 13421
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Let’s say that you are fast asleep some night and begin dreaming. In your dream, you have a time machine and a few 500-MHz four-way superscalar processors. You turn the time machine back to 1981. Once you arrive back in time, you go out and purchase an IBM PC with an Intel 8088 microprocessor running at 4.77 MHz. For much of the rest of the night, you toss and turn as you try to adapt the 500-MHz processor to the Intel 8088 socket using a soldering iron and Swiss Army knife. Just before you wake up, the new computer finally works, and you turn it on to run the Linpack1 benchmark and issue a press release. Would you expect this to turn out to be a dream or a nightmare? Chances are good that it would turn out to be a nightmare, just like the previous night where you went back to the Middle Ages and put a jet engine on a horse. (You have got to stop eating double pepperoni pizzas so late at night.)
Even if you can speed up the computational aspects of a processor infinitely fast, you still must load and store the data and instructions to and from a memory. Today’s processors continue to creep ever closer to infinitely fast processing. Memory performance is increasing at a much slower rate (it will take longer for memory to become infinitely fast). Many of the interesting problems in high performance computing use a large amount of memory. As computers are getting faster, the size of problems they tend to operate on also goes up. The trouble is that when you want to solve these problems at high speeds, you need a memory system that is large, yet at the same time fast—a big challenge. Possible approaches include the following:
- Every memory system component can be made individually fast enough to respond to every memory access request.
- Slow memory can be accessed in a round-robin fashion (hopefully) to give the effect of a faster memory system.
- The memory system design can be made “wide” so that each transfer contains many bytes of information.
- The system can be divided into faster and slower portions and arranged so that the fast portion is used more often than the slow one.
Again, economics are the dominant force in the computer business. A cheap, statistically optimized memory system will be a better seller than a prohibitively expensive, blazingly fast one, so the first choice is not much of a choice at all. But these choices, used in combination, can attain a good fraction of the performance you would get if every component were fast. Chances are very good that your high performance workstation incorporates several or all of them.
Once the memory system has been decided upon, there are things we can do in software to see that it is used efficiently. A compiler that has some knowledge of the way memory is arranged and the details of the caches can optimize their use to some extent. The other place for optimizations is in user applications, as we’ll see later in the book. A good pattern of memory access will work with, rather than against, the components of the system.
In this chapter we discuss how the pieces of a memory system work. We look at how patterns of data and instruction access factor into your overall runtime, especially as CPU speeds increase. We also talk a bit about the performance implications of running in a virtual memory environment.
Memory Technology
Almost all fast memories used today are semiconductor-based.2 They come in two flavors: dynamic random access memory (DRAM) and static random access memory (SRAM). The term random means that you can address memory locations in any order. This is to distinguish random access from serial memories, where you have to step through all intervening locations to get to the particular one you are interested in. An example of a storage medium that is not random is magnetic tape. The terms dynamic and static have to do with the technology used in the design of the memory cells. DRAMs are charge-based devices, where each bit is represented by an electrical charge stored in a very small capacitor. The charge can leak away in a short amount of time, so the system has to be continually refreshed to prevent data from being lost. The act of reading a bit in DRAM also discharges the bit, requiring that it be refreshed. It’s not possible to read the memory bit in the DRAM while it’s being refreshed.
SRAM is based on gates, and each bit is stored in four to six connected transistors. SRAM memories retain their data as long as they have power, without the need for any form of data refresh.
DRAM offers the best price/performance, as well as highest density of memory cells per chip. This means lower cost, less board space, less power, and less heat. On the other hand, some applications such as cache and video memory require higher speed, to which SRAM is better suited. Currently, you can choose between SRAM and DRAM at slower speeds — down to about 50 nanoseconds (ns). SRAM has access times down to about 7 ns at higher cost, heat, power, and board space.
In addition to the basic technology to store a single bit of data, memory performance is limited by the practical considerations of the on-chip wiring layout and the external pins on the chip that communicate the address and data information between the memory and the processor.
Access Time
The amount of time it takes to read or write a memory location is called the memory access time. A related quantity is the memory cycle time. Whereas the access time says how quickly you can reference a memory location, cycle time describes how often you can repeat references. They sound like the same thing, but they’re not. For instance, if you ask for data from DRAM chips with a 50-ns access time, it may be 100 ns before you can ask for more data from the same chips. This is because the chips must internally recover from the previous access. Also, when you are retrieving data sequentially from DRAM chips, some technologies have improved performance. On these chips, data immediately following the previously accessed data may be accessed as quickly as 10 ns.
Access and cycle times for commodity DRAMs are shorter than they were just a few years ago, meaning that it is possible to build faster memory systems. But CPU clock speeds have increased too. The home computer market makes a good study. In the early 1980s, the access time of commodity DRAM (200 ns) was shorter than the clock cycle (4.77 MHz = 210 ns) of the IBM PC XT. This meant that DRAM could be connected directly to the CPU without worrying about over running the memory system. Faster XT and AT models were introduced in the mid-1980s with CPUs that clocked more quickly than the access times of available commodity memory. Faster memory was available for a price, but vendors punted by selling computers with wait states added to the memory access cycle. Wait states are artificial delays that slow down references so that memory appears to match the speed of a faster CPU — at a penalty. However, the technique of adding wait states begins to significantly impact performance around 25?33MHz. Today, CPU speeds are even farther ahead of DRAM speeds.
The clock time for commodity home computers has gone from 210 ns for the XT to around 3 ns for a 300-MHz Pentium-II, but the access time for commodity DRAM has decreased disproportionately less — from 200 ns to around 50 ns. Processor performance doubles every 18 months, while memory performance doubles roughly every seven years.
The CPU/memory speed gap is even larger in workstations. Some models clock at intervals as short as 1.6 ns. How do vendors make up the difference between CPU speeds and memory speeds? The memory in the Cray-1 supercomputer used SRAM that was capable of keeping up with the 12.5-ns clock cycle. Using SRAM for its main memory system was one of the reasons that most Cray systems needed liquid cooling.
Unfortunately, it’s not practical for a moderately priced system to rely exclusively on SRAM for storage. It’s also not practical to manufacture inexpensive systems with enough storage using exclusively SRAM.
The solution is a hierarchy of memories using processor registers, one to three levels of SRAM cache, DRAM main memory, and virtual memory stored on media such as disk. At each point in the memory hierarchy, tricks are employed to make the best use of the available technology. For the remainder of this chapter, we will examine the memory hierarchy and its impact on performance.
In a sense, with today’s high performance microprocessor performing computations so quickly, the task of the high performance programmer becomes the careful management of the memory hierarchy. In some sense it’s a useful intellectual exercise to view the simple computations such as addition and multiplication as “infinitely fast” in order to get the programmer to focus on the impact of memory operations on the overall performance of the program.
Registers
At least the top layer of the memory hierarchy, the CPU registers, operate as fast as the rest of the processor. The goal is to keep operands in the registers as much as possible. This is especially important for intermediate values used in a long computation such as:
X = G * 2.41 + A / W - W * M
While computing the value of A divided by W, we must store the result of multiplying G by 2.41. It would be a shame to have to store this intermediate result in memory and then reload it a few instructions later. On any modern processor with moderate optimization, the intermediate result is stored in a register. Also, the value W is used in two computations, and so it can be loaded once and used twice to eliminate a “wasted” load.
Compilers have been very good at detecting these types of optimizations and efficiently making use of the available registers since the 1970s. Adding more registers to the processor has some performance benefit. It’s not practical to add enough registers to the processor to store the entire problem data. So we must still use the slower memory technology.
Caches
Once we go beyond the registers in the memory hierarchy, we encounter caches. Caches are small amounts of SRAM that store a subset of the contents of the memory. The hope is that the cache will have the right subset of main memory at the right time.
The actual cache architecture has had to change as the cycle time of the processors has improved. The processors are so fast that off-chip SRAM chips are not even fast enough. This has lead to a multilevel cache approach with one, or even two, levels of cache implemented as part of the processor. [Table 1] shows the approximate speed of accessing the memory hierarchy on a 500-MHz DEC 21164 Alpha.
| Registers | 2 ns |
| L1 On-Chip | 4 ns |
| L2 On-Chip | 5 ns |
| L3 Off-Chip | 30 ns |
| Memory | 220 ns |
When every reference can be found in a cache, you say that you have a 100% hit rate. Generally, a hit rate of 90% or better is considered good for a level-one (L1) cache. In level-two (L2) cache, a hit rate of above 50% is considered acceptable. Below that, application performance can drop off steeply.
One can characterize the average read performance of the memory hierarchy by examining the probability that a particular load will be satisfied at a particular level of the hierarchy. For example, assume a memory architecture with an L1 cache speed of 10 ns, L2 speed of 30 ns, and memory speed of 300 ns. If a memory reference were satisfied from L1 cache 75% of the time, L2 cache 20% of the time, and main memory 5% of the time, the average memory performance would be:
(0.75 * 10 ) + ( 0.20 * 30 ) + ( 0.05 * 300 ) = 28.5 ns
You can easily see why it’s important to have an L1 cache hit rate of 90% or higher.
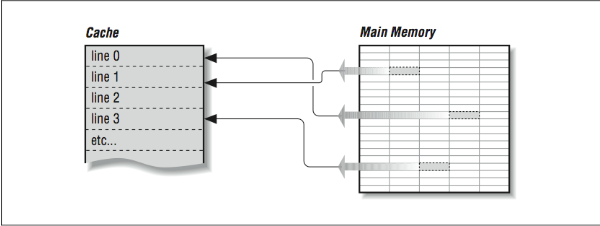
Given that a cache holds only a subset of the main memory at any time, it’s important to keep an index of which areas of the main memory are currently stored in the cache. To reduce the amount of space that must be dedicated to tracking which memory areas are in cache, the cache is divided into a number of equal sized slots known as lines. Each line contains some number of sequential main memory locations, generally four to sixteen integers or real numbers. Whereas the data within a line comes from the same part of memory, other lines can contain data that is far separated within your program, or perhaps data from somebody else’s program, as in [Figure 1]. When you ask for something from memory, the computer checks to see if the data is available within one of these cache lines. If it is, the data is returned with a minimal delay. If it’s not, your program may be delayed while a new line is fetched from main memory. Of course, if a new line is brought in, another has to be thrown out. If you’re lucky, it won’t be the one containing the data you are just about to need.
On multiprocessors (computers with several CPUs), written data must be returned to main memory so the rest of the processors can see it, or all other processors must be made aware of local cache activity. Perhaps they need to be told to invalidate old lines containing the previous value of the written variable so that they don’t accidentally use stale data. This is known as maintaining coherency between the different caches. The problem can become very complex in a multiprocessor system.3
Caches are effective because programs often exhibit characteristics that help kep the hit rate high. These characteristics are called spatial and temporal locality of reference; programs often make use of instructions and data that are near to other instructions and data, both in space and time. When a cache line is retrieved from main memory, it contains not only the information that caused the cache miss, but also some neighboring information. Chances are good that the next time your program needs data, it will be in the cache line just fetched or another one recently fetched.
Caches work best when a program is reading sequentially through the memory. Assume a program is reading 32-bit integers with a cache line size of 256 bits. When the program references the first word in the cache line, it waits while the cache line is loaded from main memory. Then the next seven references to memory are satisfied quickly from the cache. This is called unit stride because the address of each successive data element is incremented by one and all the data retrieved into the cache is used. The following loop is a unit-stride loop:
DO I=1,1000000
SUM = SUM + A(I)
END DO
When a program accesses a large data structure using “non-unit stride,” performance suffers because data is loaded into cache that is not used. For example:
DO I=1,1000000, 8
SUM = SUM + A(I)
END DO
This code would experience the same number of cache misses as the previous loop, and the same amount of data would be loaded into the cache. However, the program needs only one of the eight 32-bit words loaded into cache. Even though this program performs one-eighth the additions of the previous loop, its elapsed time is roughly the same as the previous loop because the memory operations dominate performance.
While this example may seem a bit contrived, there are several situations in which non-unit strides occur quite often. First, when a FORTRAN two-dimensional array is stored in memory, successive elements in the first column are stored sequentially followed by the elements of the second column. If the array is processed with the row iteration as the inner loop, it produces a unit-stride reference pattern as follows:
REAL*4 A(200,200)
DO J = 1,200
DO I = 1,200
SUM = SUM + A(I,J)
END DO
END DO
Interestingly, a FORTRAN programmer would most likely write the loop (in alphabetical order) as follows, producing a non-unit stride of 800 bytes between successive load operations:
REAL*4 A(200,200)
DO I = 1,200
DO J = 1,200
SUM = SUM + A(I,J)
END DO
END DO
Because of this, some compilers can detect this suboptimal loop order and reverse the order of the loops to make best use of the memory system. As we will see in [Section 1.2], however, this code transformation may produce different results, and so you may have to give the compiler “permission” to interchange these loops in this particular example (or, after reading this book, you could just code it properly in the first place).
while ( ptr != NULL ) ptr = ptr->next;
The next element that is retrieved is based on the contents of the current element. This type of loop bounces all around memory in no particular pattern. This is called pointer chasing and there are no good ways to improve the performance of this code.
A third pattern often found in certain types of codes is called gather (or scatter) and occurs in loops such as:
SUM = SUM + ARR ( IND(I) )
where the IND array contains offsets into the ARR array. Again, like the linked list, the exact pattern of memory references is known only at runtime when the values stored in the IND array are known. Some special-purpose systems have special hardware support to accelerate this particular operation.
Cache Organization
The process of pairing memory locations with cache lines is called mapping. Of course, given that a cache is smaller than main memory, you have to share the same cache lines for different memory locations. In caches, each cache line has a record of the memory address (called the tag) it represents and perhaps when it was last used. The tag is used to track which area of memory is stored in a particular cache line.
The way memory locations (tags) are mapped to cache lines can have a beneficial effect on the way your program runs, because if two heavily used memory locations map onto the same cache line, the miss rate will be higher than you would like it to be. Caches can be organized in one of several ways: direct mapped, fully associative, and set associative.
Direct-Mapped Cache
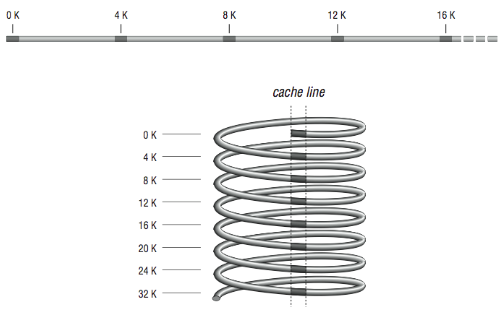
Direct mapping, as shown in [Figure 2], is the simplest algorithm for deciding how memory maps onto the cache. Say, for example, that your computer has a 4-KB cache. In a direct mapped scheme, memory location 0 maps into cache location 0, as do memory locations 4K, 8K, 12K, etc. In other words, memory maps onto the cache size. Another way to think about it is to imagine a metal spring with a chalk line marked down the side. Every time around the spring, you encounter the chalk line at the same place modulo the circumference of the spring. If the spring is very long, the chalk line crosses many coils, the analog being a large memory with many locations mapping into the same cache line.
Problems occur when alternating runtime memory references in a direct-mapped cache point to the same cache line. Each reference causes a cache miss and replaces the entry just replaced, causing a lot of overhead. The popular word for this is thrashing. When there is lots of thrashing, a cache can be more of a liability than an asset because each cache miss requires that a cache line be refilled — an operation that moves more data than merely satisfying the reference directly from main memory. It is easy to construct a pathological case that causes thrashing in a 4-KB direct-mapped cache:
REAL*4 A(1024), B(1024)
COMMON /STUFF/ A,B
DO I=1,1024
A(I) = A(I) * B(I)
END DO
END
The arrays A and B both take up exactly 4 KB of storage, and their inclusion together in COMMON assures that the arrays start exactly 4 KB apart in memory. In a 4-KB direct mapped cache, the same line that is used for A(1) is used for B(1), and likewise for A(2) and B(2), etc., so alternating references cause repeated cache misses. To fix it, you could either adjust the size of the array A, or put some other variables into COMMON, between them. For this reason one should generally avoid array dimensions that are close to powers of two.
Fully Associative Cache
At the other extreme from a direct mapped cache is a fully associative cache, where any memory location can be mapped into any cache line, regardless of memory address. Fully associative caches get their name from the type of memory used to construct them — associative memory. Associative memory is like regular memory, except that each memory cell knows something about the data it contains.
When the processor goes looking for a piece of data, the cache lines are asked all at once whether any of them has it. The cache line containing the data holds up its hand and says “I have it”; if none of them do, there is a cache miss. It then becomes a question of which cache line will be replaced with the new data. Rather than map memory locations to cache lines via an algorithm, like a direct- mapped cache, the memory system can ask the fully associative cache lines to choose among themselves which memory locations they will represent. Usually the least recently used line is the one that gets overwritten with new data. The assumption is that if the data hasn’t been used in quite a while, it is least likely to be used in the future.
Fully associative caches have superior utilization when compared to direct mapped caches. It’s difficult to find real-world examples of programs that will cause thrashing in a fully associative cache. The expense of fully associative caches is very high, in terms of size, price, and speed. The associative caches that do exist tend to be small.
Set-Associative Cache
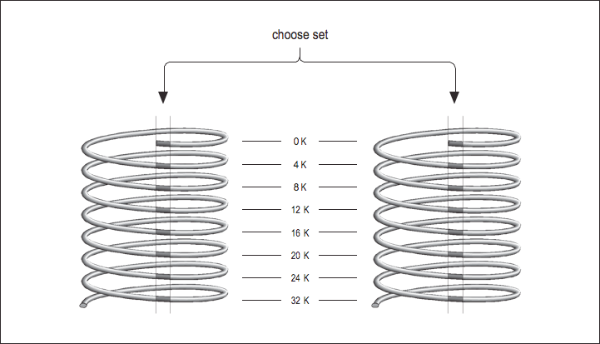
Now imagine that you have two direct mapped caches sitting side by side in a single cache unit as shown in [Figure 3]. Each memory location corresponds to a particular cache line in each of the two direct-mapped caches. The one you choose to replace during a cache miss is subject to a decision about whose line was used last — the same way the decision was made in a fully associative cache except that now there are only two choices. This is called a set-associative cache. Set-associative caches generally come in two and four separate banks of cache. These are called two-way and four-way set associative caches, respectively. Of course, there are benefits and drawbacks to each type of cache. A set-associative cache is more immune to cache thrashing than a direct-mapped cache of the same size, because for each mapping of a memory address into a cache line, there are two or more choices where it can go. The beauty of a direct-mapped cache, however, is that it’s easy to implement and, if made large enough, will perform roughly as well as a set-associative design. Your machine may contain multiple caches for several different purposes. Here’s a little program for causing thrashing in a 4-KB two-way set-associative cache:
REAL*4 A(1024), B(1024), C(1024)
COMMON /STUFF/ A,B,C
DO I=1,1024
A(I) = A(I) * B(I) + C(I)
END DO
END
Like the previous cache thrasher program, this forces repeated accesses to the same cache lines, except that now there are three variables contending for the choose set same mapping instead of two. Again, the way to fix it would be to change the size of the arrays or insert something in between them, in COMMON. By the way, if you accidentally arranged a program to thrash like this, it would be hard for you to detect it — aside from a feeling that the program runs a little slow. Few vendors provide tools for measuring cache misses.
Instruction Cache
So far we have glossed over the two kinds of information you would expect to find in a cache between main memory and the CPU: instructions and data. But if you think about it, the demand for data is separate from the demand for instructions. In superscalar processors, for example, it’s possible to execute an instruction that causes a data cache miss alongside other instructions that require no data from cache at all, i.e., they operate on registers. It doesn’t seem fair that a cache miss on a data reference in one instruction should keep you from fetching other instructions because the cache is tied up. Furthermore, a cache depends on locality of reference between bits of data and other bits of data or instructions and other instructions, but what kind of interplay is there between instructions and data? It would seem possible for instructions to bump perfectly useful data from cache, or vice versa, with complete disregard for locality of reference.
Many designs from the 1980s used a single cache for both instructions and data. But newer designs are employing what is known as the Harvard Memory Architecture, where the demand for data is segregated from the demand for instructions.
Main memory is a still a single large pool, but these processors have separate data and instruction caches, possibly of different designs. By providing two independent sources for data and instructions, the aggregate rate of information coming from memory is increased, and interference between the two types of memory references is minimized. Also, instructions generally have an extremely high level of locality of reference because of the sequential nature of most programs. Because the instruction caches don’t have to be particularly large to be effective, a typical architecture is to have separate L1 caches for instructions and data and to have a combined L2 cache. For example, the IBM/Motorola PowerPC 604e has separate 32-K four-way set-associative L1 caches for instruction and data and a combined L2 cache.
Virtual Memory
Virtual memory decouples the addresses used by the program (virtual addresses) from the actual addresses where the data is stored in memory (physical addresses). Your program sees its address space starting at 0 and working its way up to some large number, but the actual physical addresses assigned can be very different. It gives a degree of flexibility by allowing all processes to believe they have the entire memory system to themselves. Another trait of virtual memory systems is that they divide your program’s memory up into pages — chunks. Page sizes vary from 512 bytes to 1 MB or larger, depending on the machine. Pages don’t have to be allocated contiguously, though your program sees them that way. By being separated into pages, programs are easier to arrange in memory, or move portions out to disk.
Page Tables
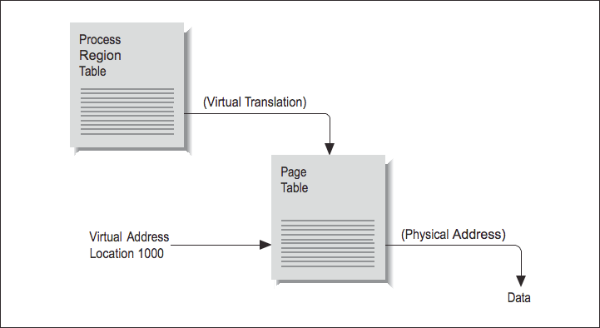
Say that your program asks for a variable stored at location 1000. In a virtual memory machine, there is no direct correspondence between your program’s idea of where location 1000 is and the physical memory systems’ idea. To find where your variable is actually stored, the location has to be translated from a virtual to a physical address. The map containing such translations is called a page table. Each process has a several page tables associated with it, corresponding to different regions, such as program text and data segments.
To understand how address translation works, imagine the following scenario: at some point, your program asks for data from location 1000. [Figure 4] shows the steps required to complete the retrieval of this data. By choosing location 1000, you have identified which region the memory reference falls in, and this identifies which page table is involved. Location 1000 then helps the processor choose an entry within the table. For instance, if the page size is 512 bytes, 1000 falls within the second page (pages range from addresses 0–511, 512–1023, 1024–1535, etc.).
Therefore, the second table entry should hold the address of the page housing the value at location 1000.
The operating system stores the page-table addresses virtually, so it’s going to take a virtual-to-physical translation to locate the table in memory. One more virtual-to- physical translation, and we finally have the true address of location 1000. The memory reference can complete, and the processor can return to executing your program.
Translation Lookaside Buffer
As you can see, address translation through a page table is pretty complicated. It required two table lookups (maybe three) to locate our data. If every memory reference was that complicated, virtual memory computers would be horrible performers. Fortunately, locality of reference causes virtual address translations to group together; a program may repeat the same virtual page mapping millions of times a second. And where we have repeated use of the same data, we can apply a cache.
All modern virtual memory machines have a special cache called a translation lookaside buffer (TLB) for virtual-to-physical-memory-address translation. The two inputs to the TLB are an integer that identifies the program making the memory request and the virtual page requested. From the output pops a pointer to the physical page number. Virtual address in; physical address out. TLB lookups occur in parallel with instruction execution, so if the address data is in the TLB, memory references proceed quickly.
Like other kinds of caches, the TLB is limited in size. It doesn’t contain enough entries to handle all the possible virtual-to-physical-address translations for all the programs that might run on your computer. Larger pools of address translations are kept out in memory, in the page tables. If your program asks for a virtual-to- physical-address translation, and the entry doesn’t exist in the TLB, you suffer a TLB miss. The information needed may have to be generated (a new page may need to be created), or it may have to be retrieved from the page table.
The TLB is good for the same reason that other types of caches are good: it reduces the cost of memory references. But like other caches, there are pathological cases where the TLB can fail to deliver value. The easiest case to construct is one where every memory reference your program makes causes a TLB miss:
REAL X(10000000)
COMMON X
DO I=0,9999
DO J=1,10000000,10000
SUM = SUM + X(J+I)
END DO
END DO
Assume that the TLB page size for your computer is less than 40 KB. Every time through the inner loop in the above example code, the program asks for data that is 4 bytes*10,000 = 40,000 bytes away from the last reference. That is, each reference falls on a different memory page. This causes 1000 TLB misses in the inner loop, taken 1001 times, for a total of at least one million TLB misses. To add insult to injury, each reference is guaranteed to cause a data cache miss as well. Admittedly, no one would start with a loop like the one above. But presuming that the loop was any good to you at all, the restructured version in the code below would cruise through memory like a warm knife through butter:
REAL X(10000000)
COMMON X
DO I=1,10000000
SUM = SUM + X(I)
END DO
The revised loop has unit stride, and TLB misses occur only every so often. Usually it is not necessary to explicitly tune programs to make good use of the TLB. Once a program is tuned to be “cache-friendly,” it nearly always is tuned to be TLB friendly.
Because there is a performance benefit to keeping the TLB very small, the TLB entry often contains a length field. A single TLB entry can be over a megabyte in length and can be used to translate addresses stored in multiple virtual memory pages.
Page Faults
A page table entry also contains other information about the page it represents, including flags to tell whether the translation is valid, whether the associated page can be modified, and some information describing how new pages should be initialized. References to pages that aren’t marked valid are called page faults.
Taking a worst-case scenario, say that your program asks for a variable from a particular memory location. The processor goes to look for it in the cache and finds it isn’t there (cache miss), which means it must be loaded from memory. Next it goes to the TLB to find the physical location of the data in memory and finds there is no TLB entry (a TLB miss). Then it tries consulting the page table (and refilling the TLB), but finds that either there is no entry for your particular page or that the memory page has been shipped to disk (both are page faults). Each step of the memory hierarchy has shrugged off your request. A new page will have to be created in memory and possibly, depending on the circumstances, refilled from disk.
Although they take a lot of time, page faults aren’t errors. Even under optimal conditions every program suffers some number of page faults. Writing a variable for the first time or calling a subroutine that has never been called can cause a page fault. This may be surprising if you have never thought about it before. The illusion is that your entire program is present in memory from the start, but some portions may never be loaded. There is no reason to make space for a page whose data is never referenced or whose instructions are never executed. Only those pages that are required to run the job get created or pulled in from the disk.4
The pool of physical memory pages is limited because physical memory is limited, so on a machine where many programs are lobbying for space, there will be a higher number of page faults. This is because physical memory pages are continually being recycled for other purposes. However, when you have the machine to yourself, and memory is less in demand, allocated pages tend to stick around for a while. In short, you can expect fewer page faults on a quiet machine. One trick to remember if you ever end up working for a computer vendor: always run short benchmarks twice. On some systems, the number of page faults will go down. This is because the second run finds pages left in memory by the first, and you won’t have to pay for page faults again.5
Paging space (swap space) on the disk is the last and slowest piece of the memory hierarchy for most machines. In the worst-case scenario we saw how a memory reference could be pushed down to slower and slower performance media before finally being satisfied. If you step back, you can view the disk paging space as having the same relationship to main memory as main memory has to cache. The same kinds of optimizations apply too, and locality of reference is important. You can run programs that are larger than the main memory system of your machine, but sometimes at greatly decreased performance. When we look at memory optimizations in [Section 2.4], we will concentrate on keeping the activity in the fastest parts of the memory system and avoiding the slow parts.
Improving Memory Performance
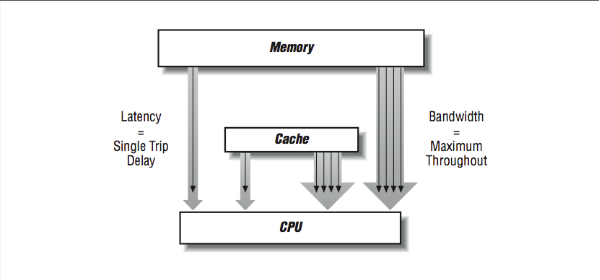
Given the importance, in the area of high performance computing, of the performance of a computer’s memory subsystem, many techniques have been used to improve the performance of the memory systems of computers. The two attributes of memory system performance are generally bandwidth and latency. Some memory system design changes improve one at the expense of the other, and other improvements positively impact both bandwidth and latency. Bandwidth generally focuses on the best possible steady-state transfer rate of a memory system. Usually this is measured while running a long unit-stride loop reading or reading and writing memory. Latency is a measure of the worst-case performance of a memory system as it moves a small amount of data such as a 32- or 64-bit word between the processor and memory. Both are important because they are an important part of most high performance applications.
Because memory systems are divided into components, there are different bandwidth and latency figures between different components as shown in [Figure 5]. The bandwidth rate between a cache and the CPU will be higher than the bandwidth between main memory and the cache, for instance. There may be several caches and paths to memory as well. Usually, the peak memory bandwidth quoted by vendors is the speed between the data cache and the processor.
In the rest of this section, we look at techniques to improve latency, bandwidth, or both.
Large Caches
As we mentioned at the start of this chapter, the disparity between CPU speeds and memory is growing. If you look closely, you can see vendors innovating in several ways. Some workstations are being offered with 4- MB data caches! This is larger than the main memory systems of machines just a few years ago. With a large enough cache, a small (or even moderately large) data set can fit completely inside and get incredibly good performance. Watch out for this when you are testing new hardware. When your program grows too large for the cache, the performance may drop off considerably, perhaps by a factor of 10 or more, depending on the memory access patterns. Interestingly, an increase in cache size on the part of vendors can render a benchmark obsolete.
Up to 1992, the Linpack 100×100 benchmark was probably the single most- respected benchmark to determine the average performance across a wide range of applications. In 1992, IBM introduced the IBM RS-6000 which had a cache large enough to contain the entire 100×100 matrix for the duration of the benchmark. For the first time, a workstation had performance on this benchmark on the same order of supercomputers. In a sense, with the entire data structure in a SRAM cache, the RS-6000 was operating like a Cray vector supercomputer. The problem was that the Cray could maintain and improve the performance for a 120×120 matrix, whereas the RS-6000 suffered a significant performance loss at this increased matrix size. Soon, all the other workstation vendors introduced similarly large caches, and the 100×100 Linpack benchmark ceased to be useful as an indicator of average application performance.
Wider Memory Systems
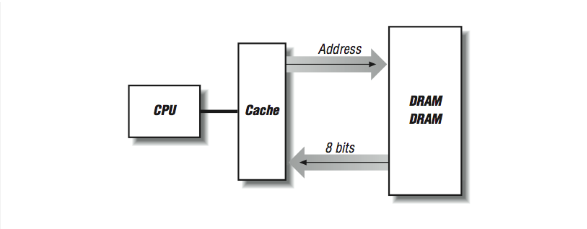
Consider what happens when a cache line is refilled from memory: consecutive memory locations from main memory are read to fill consecutive locations within the cache line. The number of bytes transferred depends on how big the line is — anywhere from 16 bytes to 256 bytes or more. We want the refill to proceed quickly because an instruction is stalled in the pipeline, or perhaps the processor is waiting for more instructions. In [Figure 6], if we have two DRAM chips that provide us with 4 bits of data every 100 ns (remember cycle time), a cache fill of a 16-byte line takes 1600 ns.
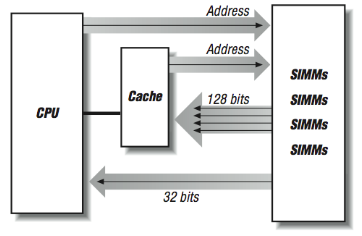
One way to make the cache-line fill operation faster is to “widen” the memory system as shown in [Figure 7]. Instead of having two rows of DRAMs, we create multiple rows of DRAMs. Now on every 100-ns cycle, we get 32 contiguous bits, and our cache-line fills are four times faster.

We can improve the performance of a memory system by increasing the width of the memory system up to the length of the cache line, at which time we can fill the entire line in a single memory cycle. On the SGI Power Challenge series of systems, the memory width is 256 bits. The downside of a wider memory system is that DRAMs must be added in multiples. In many modern workstations and personal computers, memory is expanded in the form of single inline memory modules (SIMMs). SIMMs currently are either 30-, 72-, or 168-pin modules, each of which is made up of several DRAM chips ready to be installed into a memory sub-system.
Bypassing Cache
It’s interesting that we have spent nearly an entire chapter on how great a cache is for high performance computers, and now we are going to bypass the cache to improve performance. As mentioned earlier, some types of processing result in non-unit strides (or bouncing around) through memory. These types of memory reference patterns bring out the worst-case behavior in cache-based architectures. It is these reference patterns that see improved performance by bypassing the cache. Inability to support these types of computations remains an area where traditional supercomputers can significantly outperform high-speed RISC processors. For this reason, RISC processors that are serious about number crunching may have special instructions that bypass data cache memory; the data are transferred directly between the processor and the main memory system.7 In [Figure 8] we have four banks of SIMMs that can do cache fills at 128 bits per 100 ns memory cycle. Remember that the data is available after 50 ns but we can’t get more data until the DRAMs refresh 50–60 ns later. However, if we are doing 32-bit non-unit- stride loads and have the capability to bypass cache, each load will be satisfied from one of the four SIMMs in 50 ns. While that SIMM refreshed, another load can occur from any of the other three SIMMs in 50 ns. In a random mix of non-unit loads there is a 75% chance that the next load will fall on a “fresh” DRAM. If the load falls on a bank while it is refreshing, it simply has to wait until the refresh completes.
A further advantage of bypassing cache is that the data doesn’t need to be moved through the SRAM cache. This operation can add from 10–50 ns to the load time for a single word. This also avoids invalidating the contents of an entire cache line in the cache.
Adding cache bypass, increasing memory-system widths, and adding banks increases the cost of a memory system. Computer-system vendors make an economic choice as to how many of these techniques they need to apply to get sufficient performance for their particular processor and system. Hence, as processor speed increases, vendors must add more of these memory system features to their commodity systems to maintain a balance between processor and memory-system speed.
Interleaved and Pipelined Memory Systems
Vector supercomputers, such as the CRAY Y/MP and the Convex C3, are machines that depend on multibanked memory systems for performance. The C3, in particular, has a memory system with up to 256-way interleaving. Each interleave (or bank) is 64 bits wide. This is an expensive memory system to build, but it has some very nice performance characteristics. Having a large number of banks helps to reduce the chances of repeated access to the same memory bank. If you do hit the same bank twice in a row, however, the penalty is a delay of nearly 300 ns — a long time for a machine with a clock speed of 16 ns. So when things go well, they go very well.
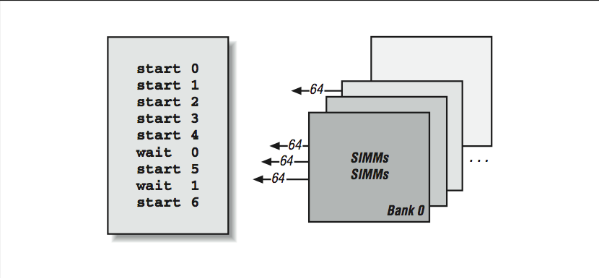
However, having a large number of banks alone is not sufficient to feed a 16-ns processor using 50 ns DRAM. In addition to interleaving, the memory subsystem also needs to be pipelined. That is, the CPU must begin the second, third, and fourth load before the CPU has received the results of the first load as shown in [Figure 9]. Then each time it receives the results from bank “n,” it must start the load from bank “n+4” to keep the pipeline fed. This way, after a brief startup delay, loads complete every 16 ns and so the memory system appears to operate at the clock rate of the CPU. This pipelined memory approach is facilitated by the 128-element vector registers in the C3 processor.
Using gather/scatter hardware, non-unit-stride operations can also be pipelined. The only difference for non-unit-stride operations is that the banks are not accessed in sequential order. With a random pattern of memory references, it’s possible to reaccess a memory bank before it has completely refreshed from a previous access. This is called a bank stall.
Different access patterns are subject to bank stalls of varying severity. For instance, accesses to every fourth word in an eight-bank memory system would also be subject to bank stalls, though the recovery would occur sooner. References to every second word might not experience bank stalls at all; each bank may have recovered by the time its next reference comes around; it depends on the relative speeds of the processor and memory system. Irregular access patterns are sure to encounter some bank stalls.
In addition to the bank stall hazard, single-word references made directly to a multibanked memory system carry a greater latency than those of (successfully) cached memory accesses. This is because references are going out to memory that is slower than cache, and there may be additional address translation steps as well. However, banked memory references are pipelined. As long as references are started well enough in advance, several pipelined, multibanked references can be in flight at one time, giving you good throughput.
The CDC-205 system performed vector operations in a memory-to-memory fashion using a set of explicit memory pipelines. This system had superior performance for very long unit-stride vector computations. A single instruction could perform 65,000 computations using three memory pipes.
Software Managed Caches
Here’s an interesting thought: if a vector processor can plan far enough in advance to start a memory pipe, why can’t a RISC processor start a cache-fill before it really needs the data in those same situations? In a way, this is priming the cache to hide the latency of the cache-fill. If this could be done far enough in advance, it would appear that all memory references would operate at the speed of the cache.
This concept is called prefetching and it is supported using a special prefetch instruction available on many RISC processors. A prefetch instruction operates just like a standard load instruction, except that the processor doesn’t wait for the cache to fill before the instruction completes. The idea is to prefetch far enough ahead of the computation to have the data ready in cache by the time the actual computation occurs. The following is an example of how this might be used:
DO I=1,1000000,8
PREFETCH(ARR(I+8))
DO J=0,7
SUM=SUM+ARR(I+J)
END DO
END DO
This is not the actual FORTRAN. Prefetching is usually done in the assembly code generated by the compiler when it detects that you are stepping through the array using a fixed stride. The compiler typically estimate how far ahead you should be prefetching. In the above example, if the cache-fills were particularly slow, the value 8 in I+8 could be changed to 16 or 32 while the other values changed accordingly.
In a processor that could only issue one instruction per cycle, there might be no payback to a prefetch instruction; it would take up valuable time in the instruction stream in exchange for an uncertain benefit. On a superscalar processor, however, a cache hint could be mixed in with the rest of the instruction stream and issued alongside other, real instructions. If it saved your program from suffering extra cache misses, it would be worth having.
Post-RISC Effects on Memory References
Memory operations typically access the memory during the execute phase of the pipeline on a RISC processor. On the post-RISC processor, things are no different than on a RISC processor except that many loads can be half finished at any given moment. On some current processors, up to 28 memory operations may be active with 10 waiting for off-chip memory to arrive. This is an excellent way to compensate for slow memory latency compared to the CPU speed. Consider the following loop:
LOADI R6,10000 Set the Iterations
LOADI R5,0 Set the index variable
LOOP: LOAD R1,R2(R5) Load a value from memory
INCR R1 Add one to R1
STORE R1,R3(R5) Store the incremented value back to memory
INCR R5 Add one to R5
COMPARE R5,R6 Check for loop termination
BLT LOOP Branch if R5 < R6 back to LOOP
In this example, assume that it take 50 cycles to access memory. When the fetch/ decode puts the first load into the instruction reorder buffer (IRB), the load starts on the next cycle and then is suspended in the execute phase. However, the rest of the instructions are in the IRB. The INCR R1 must wait for the load and the STORE must also wait. However, by using a rename register, the INCR R5, COMPARE, and BLT can all be computed, and the fetch/decode goes up to the top of the loop and sends another load into the IRB for the next memory location that will have to wait. This looping continues until about 10 iterations of the loop are in the IRB. Then the first load actually shows up from memory and the INCR R1 and STORE from the first iteration begins executing. Of course the store takes a while, but about that time the second load finishes, so there is more work to do and so on…
Like many aspects of computing, the post-RISC architecture, with its out-of-order and speculative execution, optimizes memory references. The post-RISC processor dynamically unrolls loops at execution time to compensate for memory subsystem delay. Assuming a pipelined multibanked memory system that can have multiple memory operations started before any complete (the HP PA-8000 can have 10 off- chip memory operations in flight at one time), the processor continues to dispatch memory operations until those operations begin to complete.
Unlike a vector processor or a prefetch instruction, the post-RISC processor does not need to anticipate the precise pattern of memory references so it can carefully control the memory subsystem. As a result, the post-RISC processor can achieve peak performance in a far-wider range of code sequences than either vector processors or in-order RISC processors with prefetch capability.
This implicit tolerance to memory latency makes the post-RISC processors ideal for use in the scalable shared-memory processors of the future, where the memory hierarchy will become even more complex than current processors with three levels of cache and a main memory.
Unfortunately, the one code segment that doesn’t benefit significantly from the post-RISC architecture is the linked-list traversal. This is because the next address is never known until the previous load is completed so all loads are fundamentally serialized.
Dynamic RAM Technology Trends
Much of the techniques in this section have focused on how to deal with the imperfections of the dynamic RAM chip (although when your clock rate hits 300–600 MHz or 3–2 ns, even SRAM starts to look pretty slow). It’s clear that the demand for more and more RAM will continue to increase, and gigabits and more DRAM will fit on a single chip. Because of this, significant work is underway to make new super-DRAMs faster and more tuned to the extremely fast processors of the present and the future. Some of the technologies are relatively straightforward, and others require a major redesign of the way that processors and memories are manufactured.
Some DRAM improvements include:
- Fast page mode DRAM
- Extended data out RAM (EDO RAM)
- Synchronous DRAM (SDRAM)
- RAMBUS
- Cached DRAM (CDRAM)
Fast page mode DRAM saves time by allowing a mode in which the entire address doesn’t have to be re-clocked into the chip for each memory operation. Instead, there is an assumption that the memory will be accessed sequentially (as in a cache-line fill), and only the low-order bits of the address are clocked in for successive reads or writes.
EDO RAM is a modification to output buffering on page mode RAM that allows it to operate roughly twice as quickly for operations other than refresh.
Synchronous DRAM is synchronized using an external clock that allows the cache and the DRAM to coordinate their operations. Also, SDRAM can pipeline the retrieval of multiple memory bits to improve overall throughput.
RAMBUS is a proprietary technology capable of 500 MB/sec data transfer. RAMBUS uses significant logic within the chip and operates at higher power levels than typical DRAM.
Cached DRAM combines a SRAM cache on the same chip as the DRAM. This tightly couples the SRAM and DRAM and provides performance similar to SRAM devices with all the limitations of any cache architecture. One advantage of the CDRAM approach is that the amount of cache is increased as the amount of DRAM is increased. Also when dealing with memory systems with a large number of interleaves, each interleave has its own SRAM to reduce latency, assuming the data requested was in the SRAM.
An even more advanced approach is to integrate the processor, SRAM, and DRAM onto a single chip clocked at say 5 GHz, containing 128 MB of data. Understandably, there is a wide range of technical problems to solve before this type of component is widely available for $200 — but it’s not out of the question. The manufacturing processes for DRAM and processors are already beginning to converge in some ways (RAMBUS). The biggest performance problem when we have this type of system will be, “What to do if you need 160 MB?”
Closing Notes
They say that the computer of the future will be a good memory system that just happens to have a CPU attached. As high performance microprocessor systems take over as the high performance computing engines, the problem of a cache-based memory system that uses DRAM for main memory must be solved. There are many architecture and technology efforts underway to transform workstation and personal computer memories to be as capable as supercomputer memories.
As CPU speed increases faster than memory speed, you will need the techniques in this book. Also, as you move into multiple processors, memory problems don’t get better; usually they get worse. With many hungry processors always ready for more data, a memory subsystem can become extremely strained.
With just a little skill, we can often restructure memory accesses so that they play to your memory system’s strengths instead of its weaknesses.
Exercises
Exercise \(\PageIndex{1}\)
The following code segment traverses a pointer chain: while ((p = (char *) *p) != NULL); How will such a code interact with the cache if all the references fall within a small portion of memory? How will the code interact with the cache if references are stretched across many megabytes?
Exercise \(\PageIndex{2}\)
How would the code in [Exercise 1] behave on a multibanked memory system that has no cache?
Exercise \(\PageIndex{3}\)
A long time ago, people regularly wrote self-modifying code — programs that wrote into instruction memory and changed their own behavior. What would be the implications of self-modifying code on a machine with a Harvard memory architecture?
Exercise \(\PageIndex{4}\)
Assume a memory architecture with an L1 cache speed of 10 ns, L2 speed of 30 ns, and memory speed of 200 ns. Compare the average memory system performance with (1) L1 80%, L2 10%, and memory 10%; and (2) L1 85% and memory 15%.
Exercise \(\PageIndex{5}\)
On a computer system, run loops that process arrays of varying length from 16 to 16 million: ARRAY(I) = ARRAY(I) + 3 How does the number of additions per second change as the array length changes? Experiment with REAL*4, REAL*8, INTEGER*4, and INTEGER*8.
Which has more significant impact on performance: larger array elements or integer versus floating-point? Try this on a range of different computers.
Exercise \(\PageIndex{6}\)
Create a two-dimensional array of 1024×1024. Loop through the array with rows as the inner loop and then again with columns as the inner loop. Perform a simple operation on each element. Do the loops perform differently? Why? Experiment with different dimensions for the array and see the performance impact.
Exercise \(\PageIndex{7}\)
Write a program that repeatedly executes timed loops of different sizes to determine the cache size for your system.
Footnotes
- See Chapter 15, Using Published Benchmarks, for details on the Linpack benchmark.
- Magnetic core memory is still used in applications where radiation “hardness” — resistance to changes caused by ionizing radiation — is important.
- [Section 3.2.1] describes cache coherency in more detail.
- The term for this is demand paging.
- Text pages are identified by the disk device and block number from which they came.
- See the STREAM section in Chapter 15 for measures of memory bandwidth.
- By the way, most machines have uncached memory spaces for process synchronization and I/O device registers. However, memory references to these locations bypass the cache because of the address chosen, not necessarily because of the instruction chosen.


