12.6: Coloring Planar Graphs

We’ve covered a lot of ground with planar graphs, but not nearly enough to prove the famous 4-color theorem. But we can get awfully close. Indeed, we have done almost enough work to prove that every planar graph can be colored using only 5 colors.

There are two familiar facts about planarity that we will need.

Lemma 12.6.1. Any subgraph of a planar graph is planar.

Lemma 12.6.2. Merging two adjacent vertices of a planar graph leaves another planar graph.

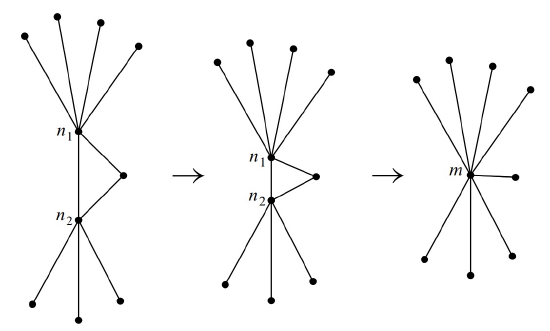
Merging two adjacent vertices, \(n_1\) and \(n_2\) of a graph means deleting the two vertices and then replacing them by a new “merged” vertex, \(m\), adjacent to all the vertices that were adjacent to either of \(n_1\) or \(n_2\), as illustrated in Figure 12.12.

Figure 12.12 Merging adjacent vertices \(n_1\) and \(n_2\) into new vertex, \(m\).

Many authors take Lemmas 12.6.1 and 12.6.2 for granted for continuous drawings of planar graphs described by Definition 12.2.1. With the recursive Definition 12.2.2 both Lemmas can actually be proved using structural induction (see Problem 12.9).

We need only one more lemma:

Lemma 12.6.3. Every planar graph has a vertex of degree at most five.

Proof. Assuming to the contrary that every vertex of some planar graph had degree at least 6, then the sum of the vertex degrees is at least \(6v\). But the sum of the vertex degrees equals \(2e\) by the Handshake Lemma 11.2.1, so we have \(e \geq 3v\) contradicting the fact that \(e \leq 3v - 6 < 3v\) by Theorem 12.4.3. \(\quad \blacksquare\)

Theorem \(\PageIndex{4}\)

Every planar graph is five-colorable.

Proof

The proof will be by strong induction on the number, \(v\), of vertices, with induction hypothesis:

Every planar graph with \(v\) vertices is five-colorable.

Base cases (\(v \leq 5\)): immediate.

Inductive case: Suppose \(G\) is a planar graph with \(v + 1\) vertices. We will describe a five-coloring of \(G\).

First, choose a vertex, \(g\), of \(G\) with degree at most 5; Lemma 12.6.3 guarantees there will be such a vertex.

Case 1: (\(\text{deg}(g) < 5\)): Deleting \(g\) from \(G\) leaves a graph, \(H\), that is planar by Lemma 12.6.1, and, since \(H\) has \(v\) vertices, it is five-colorable by induction hypothesis. Now define a five coloring of \(G\) as follows: use the five-coloring of \(H\) for all the vertices besides \(g\), and assign one of the five colors to \(g\) that is not the same as the color assigned to any of its neighbors. Since there are fewer than 5 neighbors, there will always be such a color available for \(g\).

Case 2: (\(\text{deg}(g) = 5\)): If the five neighbors of \(g\) in \(G\) were all adjacent to each other, then these five vertices would form a nonplanar subgraph isomorphic to \(K_5\), contradicting Lemma 12.6.1 (since \(K_5\) is not planar). So there must be two neighbors, \(n_1\) and \(n_2\), of \(g\) that are not adjacent. Now merge \(n_1\) and \(g\) into a new vertex, \(m\). In this new graph, \(n_2\) is adjacent to \(m\), and the graph is planar by Lemma 12.6.2. So we can then merge \(m\) and \(n_2\) into a another new vertex, \(m'\), resulting in a new graph, \(G'\), which by Lemma 12.6.2 is also planar. Since \(G'\) has \(v\) 1 vertices, it is five-colorable by the induction hypothesis.

Now define a five coloring of \(G\) as follows: use the five-coloring of \(G'\) for all the vertices besides \(g, n_1\) and \(n_2\). Next assign the color of \(m'\) in \(G'\) to be the color of the neighbors \(n_1\) and \(n_2\). Since \(n_1\) and \(n_2\) are not adjacent in \(G\), this defines a proper five-coloring of \(G\) except for vertex \(g\). But since these two neighbors of \(g\) have the same color, the neighbors of \(g\) have been colored using fewer than five colors altogether. So complete the five-coloring of \(G\) by assigning one of the five colors to \(g\) that is not the same as any of the colors assigned to its neighbors. \(\quad \blacksquare\)