6.1: Slow Saturable Absorber Mode Locking
- Page ID
- 44661
Due to the small cross section for stimulated emission in solid state lasers, typical intracavity pulse energies are much smaller than the saturation energy of the gain. Therefore, we neglected the effect of gain saturation due to one pulse sofar, the gain only saturates with the average power. However, there are gain media which have large gain cross sections like semiconductors and dyes, see Table 4.1, and typical intracavity pulse energies may become large enough to saturate the gain considerably in a single pass. In fact, it is this effect, which made the mode-locked dye laser so sucessful. The model for the slow saturable absorber mode locking has to take into account the change of gain in the passage of one pulse [1, 2]. In the following, we consider a modelocked laser, that experiences in one round-trip a saturable gain and a slow saturable absorber. In the dye laser, both media are dyes with different saturation intensities or with different focusing into the dye jets so that gain and loss may show different saturation energies. The relaxation equation of the gain, in the limit of a pulse short compared with its relaxation time, can be approximated by
\[\dfrac{dg}{dt} = -g \dfrac{|A(t)|^2}{E_L} \nonumber \]
The coefficient \(E_L\) is the saturation energy of the gain. Integration of the equation shows, that the gain saturates with the pulse energy \(E(t)\)
\[E(t) = \int_{T_{R/2}}^t dt|A(t)|^2 \nonumber \]
when passing the gain
\[g(t) = g_i \exp [-E(t)/E_L] \nonumber \]
where \(g_i\) is the initial small signal gain just before the arrival of the pulse. A similar equation holds for the loss of the saturable absorber whose response (loss) is represented by \(q(t)\)
\[g(t) = q_0 \exp [-E(t)/E_A] \nonumber \]
where \(E_A\) is the saturation energy of the saturable absorber. If the background loss is denoted by \(l\), the master equation of mode-locking becomes
\[\dfrac{1}{T_R} \dfrac{\partial}{\partial T} A = [g_i (\exp (-E(t)/E_L)) A - l A - q_0 \exp (-E(t)/E_A)]A + \dfrac{1}{\Omega_f^2} \dfrac{\partial^2}{\partial t^2} A\label{eq6.1.5} \]
Here, we have replaced the filtering action of the gain \(D_g = \dfrac{1}{\Omega_f^2}\) as produced by a separate fixed filter. An analytic solution to this integro-differential equation can be obtained with one approximation: the exponentials are expanded to second order. This is legitimate if the population depletions of the gain and saturable absorber media are not excessive. Consider one of these expansions:
\[q_0 \exp (-E(t)/E_A) \approx q_0 [ 1 - (E(t)/E_A) + \dfrac{1}{2} (E(t)/E_A)^2].\label{eq6.1.6} \]
We only consider the saturable gain and loss and the finite gain bandwidth. Than the master equation is given by
\[T_R \dfrac{\partial A(T, t)}{\partial T} = \left [ g(t) - q(t) - l + D_f \dfrac{\partial ^2}{\partial t^2} \right ] A(T, t). \nonumber \]
The filter dispersion, \(D_f = 1/\Omega_f^2\), effectively models the finite bandwidth of the laser, that might not be only due to the finite gain bandwidth, but includes all bandwidth limiting effects in a parabolic approximation. Suppose the pulse is a symmetric function of time. Then the first power of the integral gives an antisymmetric function of time, its square is symmetric. An antisymmetric function acting on the pulse \(A(t)\) causes a displacement. Hence, the steady state solution does not yield zero for the change per pass, the derivative \(\dfrac{1}{T_R} \dfrac{\partial A}{\partial T}\) must be equated to a time shift \(\Delta t\) of the pulse. When this is done one can confirm easily that \(A(t) = A_o \text{sech}(t/\tau)\) is a solution of (\(\ref{eq6.1.6}\)) with constraints on its coefficients. Thus we, are looking for a "steady state" solution \(A(t, T ) = A_o \text{sech}(\tfrac{t}{\tau} + \alpha \tfrac{T}{T_R})\). Note, that α is the fraction of the pulsewidth, the pulse is shifted in each round-trip due to the shaping by loss and gain. The constraints on its coefficients can be easily found using the following relations for the sech-pulse
\[E(t) = \int_{-T_{R/2}}^t dt |A(t)|^2 = \dfrac{W}{2} \left (1 + \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) \nonumber \]
\[E(t)^2 = \left (\dfrac{W}{2} \right )^2 \left (2 + 2 \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) - \text{sech}^2 (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) \nonumber \]
\[T_R \dfrac{\partial}{\partial T} A(t, T) = -\alpha \text{tanh} (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) A(t, T) \nonumber \]
\[\dfrac{1}{\Omega_f^2} \dfrac{\partial^2}{\partial t^2} A(t, T) = \dfrac{1}{\Omega_f^2 \tau^2} \left ( 1 - 2 \text{sech}^2 (\dfrac{t}{\tau} + \alpha \dfrac{T}{T_R}) \right ) A(t, T). \nonumber \]
substituing them into the master equation (\(\ref{eq6.1.5}\)) and collecting the coefficients in front of the different temporal functions. The constant term gives the necessary small signal gain
\[g_i \left [1 - \dfrac{W}{2E_L} + \left (\dfrac{W}{2E_L} \right )^2 \right ] = l + q_0 \left [1 - \dfrac{W}{2E_L} + \left (\dfrac{W}{2E_L} \right )^2 \right ] - \dfrac{1}{\Omega_f^2 \tau^2}.\label{eq6.1.12} \]
The constant in front of the odd tanh−function delivers the timing shift per round-trip
\[\alpha = \dfrac{\Delta}{\tau} = g_i \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ]-q_0 \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ]. \nonumber \]
And finally the constant in front of the \(\text{sech}^2\)-function determines the pulsewidth
\[\dfrac{1}{\tau^2} = \dfrac{\Omega_f^2 W^2}{8} \left (\dfrac{q_0}{E_A^2} - \dfrac{g_i}{E_L^2} \right )\label{eq6.1.14} \]
These equations have important implications. Consider first the equation for the inverse pulsewidth, (6.14). In order to get a real solution, the right hand side has to be positive. This implies that \(q_0/E_A^2 > g_i/E_L^2\). The saturable absorber must saturate more easily, and, therefore more strongly, than the gain medium in order to open a net window of gain (Figure 6.2).
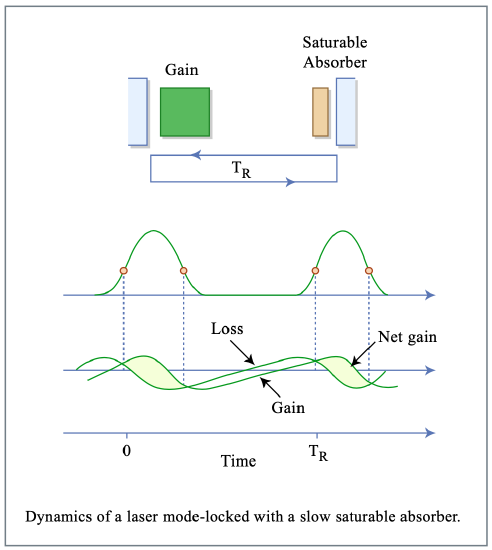
Figure by MIT OCW.
This was accomplished in a dye laser system by stronger focusing into the saturable absorber-dye jet (Reducing the saturation energy for the saturable absorber) than into the gain-dye jet (which was inverted, i.e. optically pumped). Equation (\(\ref{eq6.1.12}\)) makes a statement about the net gain before passage of the pulse. The net gain before passage of the pulse is
\[g_i - q_0 - l = -\dfrac{1}{\Omega_f^2 \tau^2} + g_i \left [\dfrac{W}{2E_L} - \left (\dfrac{W}{2E_L} \right )^2 \right ] - q_0 \left [\dfrac{W}{2E_A} - \left (\dfrac{W}{2E_A} \right )^2 \right ]. \nonumber \]
Using condition (\(\ref{eq6.1.14}\)) this can be expressed as
\[g_i - g_0 - l = g_i \left [\dfrac{W}{2E_L} \right ] - q_0 \left [ \dfrac{W}{2E_A}\right ] + \dfrac{1}{\Omega_f^2 \tau^2}. \nonumber \]
This gain is negative since the effect of the saturable absorber is larger than that of the gain. Since the pulse has the same exponential tail after passage as before, one concludes that the net gain after passage of the pulse is the same as before passage and thus also negative. The pulse is stable against noise build-up both in its front and its back. This principle works if the ratio between the saturation energies for the saturable absorber and gain \(\chi_P = E_A/E_P\) is very small. Then the shortest pulsewidth achievable with a given system is
\[\tau = \dfrac{4}{\sqrt{q_0} \Omega_f} \dfrac{E_A}{W} > \dfrac{2}{\sqrt{q_0} \Omega_f}. \nonumber \]
The greater sign comes from the fact that our theory is based on the expansion of the exponentials, which is only true for \(\dfrac{W}{2E_A} < 1\). If the filter dispersion \(1/\Omega_f^2\) that determines the bandwidth of the system is again replaced by an average gain dispersion \(g/\Omega_g^2\) and assuming \(g = q_0\). Note that the modelocking principle of the dye laser is a very faszinating one due to the fact that actually non of the elements in the system is fast. It is the interplay between two media that opens a short window in time on the scale of femtoseconds. The media themselves just have to be fast enough to recover completely between one round trip, i.e. on a nanosecond timescale.
Over the last fifteen years, the dye laser has been largely replaced by solid state lasers, which offer even more bandwidth than dyes and are on top of that much easier to handle because they do not show degradation over time. With it came the need for a different mode locking principle, since the saturation energy of these broadband solid-state laser media are much higher than the typical intracavity pulse energies. The absorber has to open and close the net gain window.


