8.8: Problems
- Page ID
- 18990
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)8.1. In a \(1 mm^3\) volume, \(10^{15}\) atoms of argon are at a temperature of \(T = 300\) K. Calculate the pressure of the gas.
8.2. Argon gas is enclosed in a container of a fixed volume. At \(T = 300\) K, the pressure of the gas is 50,000 Pa. At \(T = 350\) K, calculate the pressure of the gas.
8.3. A balloon is filled with helium atoms at room temperature, \(72 ^{\circ}F\). It has a volume of \(5 \cdot 10^{-5} m^3\), and the gas in the balloon has a pressure of \(10^6 \frac{N} {m^2}\). How many helium atoms are in the balloon, and what is the mass of the gas?
8.4. A resistive heater is used to supply heat into an insulated box. The heater has current \(0.04 A\) and resistance \(1 k\Omega\), and it operates for one hour. Energy is either stored in the box or used to spin a shaft. If the box gains 2,500 J of energy in that one hour, how much energy was used to turn the shaft?
8.5. Qualitatively, explain the difference between each pair of related quantities.
(a) Seebeck effect and Peltier effect
(b) Thermal conductivity and electrical conductivity
8.6. Match the description with the quantity measured.
| A. Electrical conductivity |
| B. Peltier coefficient |
| C. Seebeck coefficient |
| D. Thermal conductivity |
| E. Thomson coefficient |
| 1. A bar is made from a junction of two metals. A current of 1 mA is placed through the bar. The temperature at each end of the bar is measured as a function of time. The rate of heat generated across the bar divided by the current is what quantity? |
| 2. A bar is made from a junction of two metals. One end of the bar is held at a temperature of \(20 ^{\circ}C\) while the other is held at \(45 ^{\circ}C\). The voltage between the ends of the bar is measured with a voltmeter. This voltage divided by \(15 ^{\circ}C\) is what quantity? |
| 3. One end of a metal bar of is held at \(45 ^{\circ}C\) while the other end is held at \(20 ^{\circ}C\). A current of 1 mA is placed through the bar. The rate of heat generated across the bar is measured. The rate of heat generated divided by the product of 1 mA and \(1 ^{\circ}C\) is which quantity? |
| 4. One end of a metal bar of cross sectional area \(A\) is heated to a temperature of \(45 ^{\circ}C\). A thermocouple is placed 3 cm down the bar away from the heater. The product of the power dissipated in the heater times 3 cm divided by the product of A and temperature difference measured is what quantity? |
| 5. A current of 1 mA is put through a metal bar of cross sectional area \(A\). The voltage drop across the bar is measured with a voltmeter. The current times the length of the bar divided by the product of the voltage measured and \(A\) is what quantity? |
8.7. Explain how to measure each of the following quantities, and list the tools needed to make the measurement.
(a) Electrical conductivity
(b) Thermal conductivity
(c) Peltier coefficient
8.8. A thermoelectric device has a figure of merit of \(Z = 0.7 K^{-1}\). A second device is made out of the same semiconducting materials, but it has been doped so that the electrical conductivity is 20% higher. Find the figure of merit of the second device.
8.9. A thermoelectric device is made from a material with resistivity \(5 \cdot 10^{-8} \Omega \cdot m\) and Seebeck coefficient \(8.5 \cdot 10^{-5} \frac{V}{K}\). A cube, 1 cm on each side, was used to determine the thermal conductivity. One side of the cube was heated. At a steady state, the rate of energy transfer by conduction through the cube is 1.8 W. The temperature distribution through the material is linear, and a temperature difference across is measured to be 20 K across the cube. Find the thermal conductivity \(\kappa\), and find the figure of merit \(Z\) for the material.
8.10. As shown in Fig. 8.5.2, a heater supplies heat to one side of an iron rod. The rod is cylindrical with length 30 cm and radius 2 cm. The heater supplies 2 W of power to the edge of the rod. Iron has a thermal conductivity of \(\kappa = 80 \frac{W}{m \cdot K}\). Two thermocouples are are spaced 15 cm apart as shown in the figure. What is the difference in temperature (in degrees Celsius) measured between the two thermocouples?
8.11. A thermoelectric device is used to build a small refrigerator that can hold two pop cans. When the device is operating, the cold side of the device is at \(T = 10 ^{\circ}C\) while the hot side of the device, outside the refrigerator, is at \(T = 42 ^{\circ}C\). What is the maximum possible efficiency of this device?
8.12. The cold side of a thermoelectric device, used to generate electricity, is at a temperature of \(100 ^{\circ}C\). What is the minimum temperature of the hot side of the device needed to achieve an efficiency of \(\eta_{ef\,f}\) = 15%?
8.13. The Carnot efficiency describes the limit of the efficiency for some devices. Does it apply to the following types of devices? (Answer yes or no.)
- Hall effect device
- Semiconductor laser
- Photovoltaic device
- Piezoelectric device
- Pyroelectric device
- Thermoelectric device used as a temperature sensor
- Thermoelectric device used as a refrigerator
- Thermoelectric device used to generate electricity for a sensor system
8.14. The figures show Seebeck coefficient \($(T)\), electrical resistivity \(\rho(T)\) = \(\frac{1} {\sigma(T)}\), and thermal conductivity \(\kappa(T)\) plotted versus temperature \(T\) for a family of materials known as skutterudites. These materials have the composition Tl\(_x\)Co\(_{4-y}\)Fe\(_y\)Sb\(_{12}\) and Tl\(_x\)Co\(_4\)Sb\(_{12-y}\)Sn\(_y\) where \(x\) and \(y\) range from zero to 1. The figures used with permission from reference [121]. Recently, scientists have been studying the possibility of making thermoelectric devices from these materials. Using the data in the figures, approximate the thermoelectric figure of merit \(Z\) in units \(K^{-1}\) at a temperature of \(T = 200\) K for the material with \(x = 0.1\).
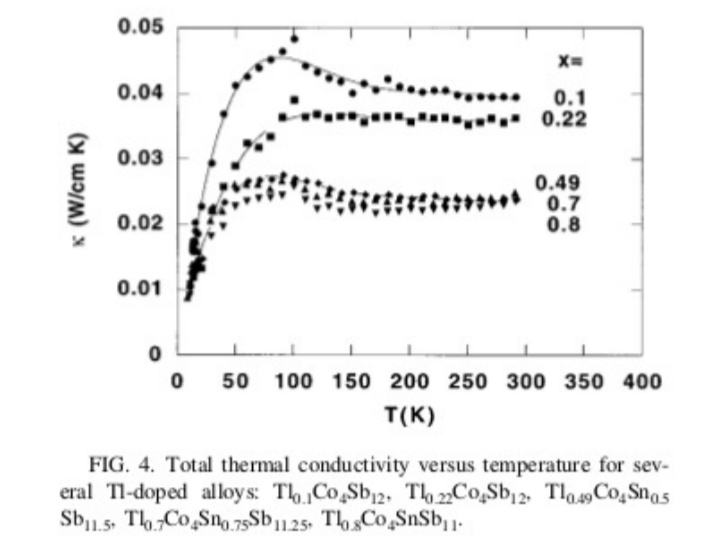
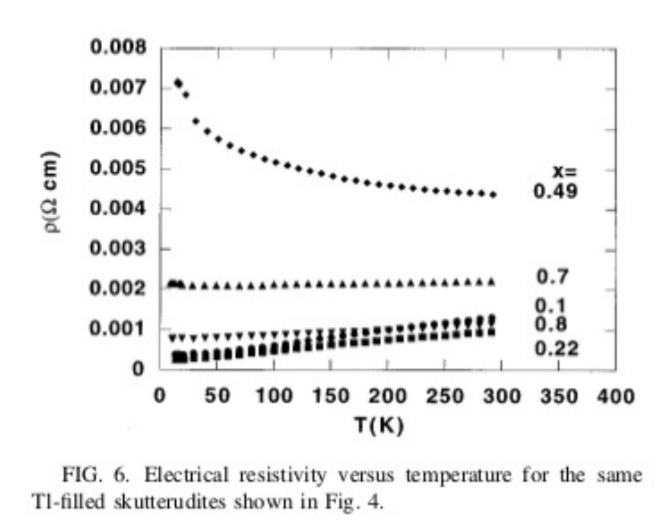
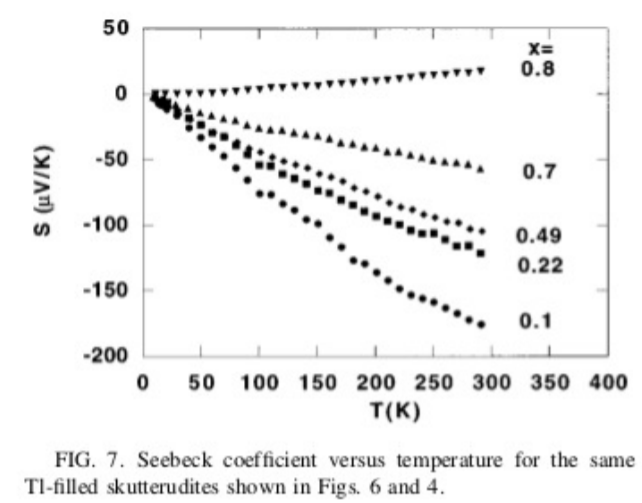
Figure \(\PageIndex{1}\)
8.15. Consider the data in the figures of the previous problem over the range \(50 < T < 300\) K for the material with \(x = 0.1\). At what temperature, within this range, is the product of the figure of merit times the temperature, \(ZT\), the largest, and what is the corresponding value of \(ZT\)? Show your work.
8.16. The figures show the Seebeck coefficient, electrical resistivity, and thermal conductivity for three different materials. Assume that we would like to use these materials to build thermoelectric devices which generate electricity where the cold side of the device is slightly below \(T \approx 400\) K, and the hot side is slightly above \(T \approx 400\) K. The figures are used with permission from reference [122].
(a) Approximately, calculate the Peltier coefficient and the Thomson coefficient for CeFe\(_4\)As\(_{12}\) near \(T \approx 400\) K.
(b) Assume you have a cube of CeFe\(_4\)As\(_{12}\), 1 cm on each side. What is the resistance R of the cube?
(c) What is the thermoelectric figure of merit \(Z\) for CeFe\(_4\)As\(_{12}\) near \(T \approx 400\) K. Include units in your answer.
(d) All else equal, which of the three materials would produce the largest voltage for a given temperature difference. Justify your answer.
(e) Which of the three materials has the largest thermoelectric figure of merit? Justify your answer.
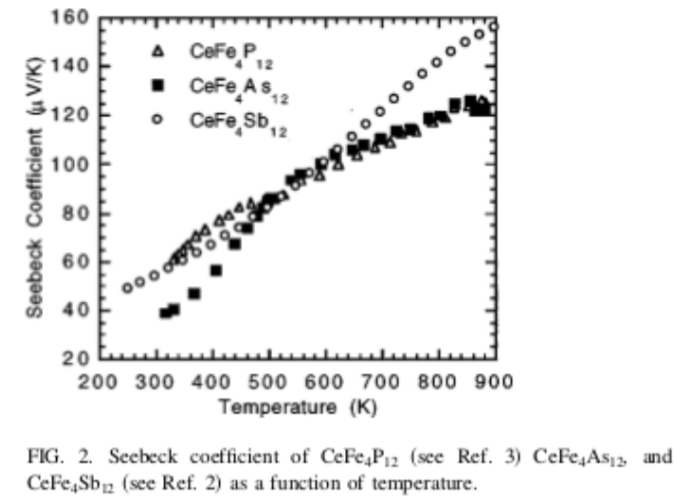
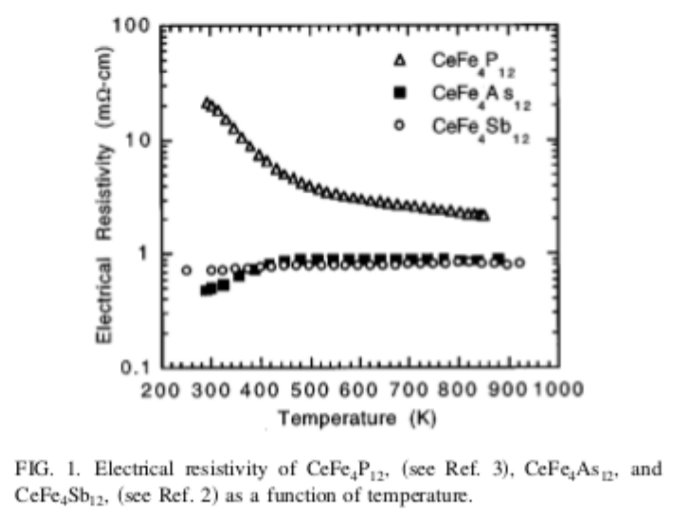
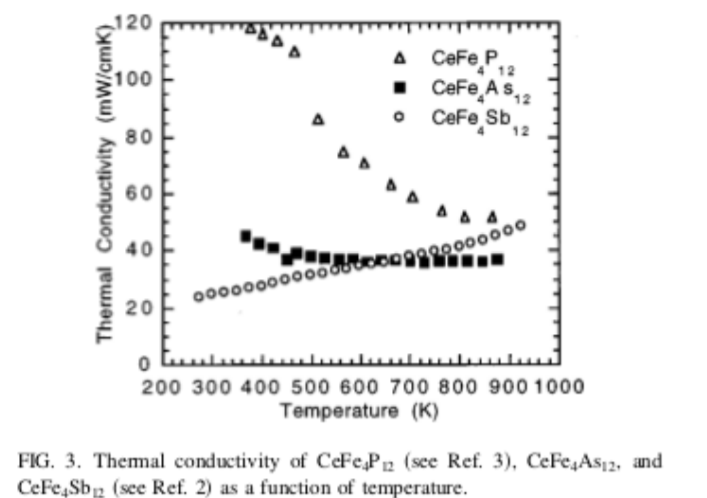
Figure \(\PageIndex{2}\)


