2.2: Complex Exponential Notation

Start by recognizing a geometric interpretation for a complex number. If we plot the real part on the horizontal (x) axis and the imaginary part on the vertical (y) axis, then the complex number \(\ \underline{z}=x+j y\) (where \(\ j=\sqrt{-1}\)) represents a vector as shown in Figure 1. Note that this vector may be represented not only by its real and imaginary components, but also by a magnitude and a phase angle:

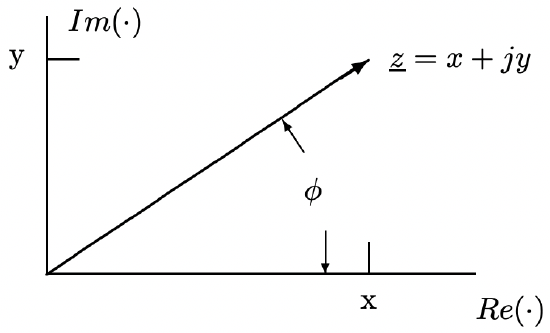Figure 1: Representation of the complex number \(\ \underline{z}=x+j y\)

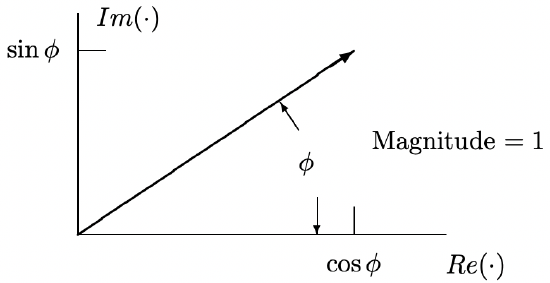Figure 2: Representation of \(\ e^{j \phi}\)

\[\ |\underline{z}|=\sqrt{x^{2}+y^{2}}\label{1} \]

\[\ \phi=\arctan \left(\frac{y}{x}\right)\label{2} \]

The basis for complex exponential notation is the celebrated Euler Relation:

\[\ e^{j \phi}=\cos (\phi)+j \sin (\phi)\label{3} \]

which has a representation as shown in Figure 2.

Now, a comparison of Figures 1 and 2 makes it clear that, with definitions (1) and (2),

\[\ \underline{z}=x+j y=|\underline{z}| e^{j \phi}\label{4} \]

It is straightforward, using (3) to show that:

\[\ \cos (\phi)=\frac{e^{j \phi}+e^{-j \phi}}{2}\label{5} \]

\[\ \sin (\phi)=\frac{e^{j \phi}-e^{-j \phi}}{2 j}\label{6} \]

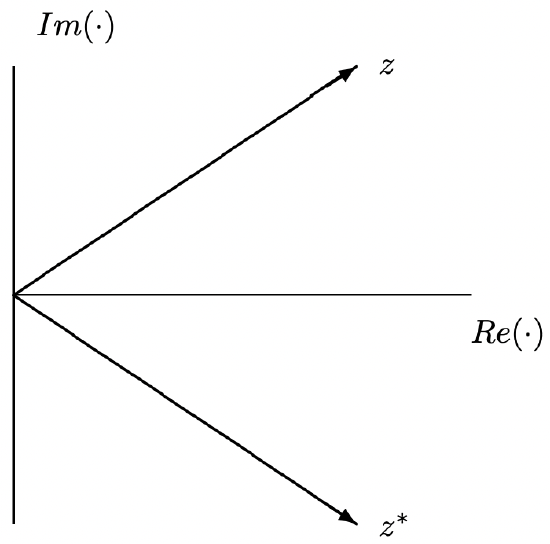Figure 3: Representation Of A Complex Number And Its Conjugate

The complex exponential is a tremendously useful type of function. Note that the product of two numbers expressed as exponenentials is the same as the exponential of the sums of the two exponents:

\[\ e^{a} e^{b}=e^{a+b}\label{8} \]

Note that it is also true that the reciprocal of a number in exponential notation is just the exponential of the negative of the exponent:

\[\ \frac{1}{e^{a}}=e^{-a}\label{9} \]

Then, if we have two numbers \(\ \underline{z}_{1}=\left|\underline{z}_{1}\right| e^{j \phi_{1}}\) and \(\ \underline{z}_{2}=\left|\underline{z}_{2}\right| e^{j \phi_{2}}\), then the product of the two numbers is:

\[\ \underline{z}_{1} \underline{z}_{2}=\left|\underline{z}_{1} \| \underline{z}_{2}\right| e^{j\left(\phi_{1}+\phi_{2}\right)}\label{10} \]

and the ratio of the two numbers is:

\[\ \frac{\underline{z}_{1}}{\underline{z}_{2}}=\frac{\left|\underline{z}_{1}\right|}{\left|\underline{z}_{2}\right|} e^{j\left(\phi_{1}-\phi_{2}\right)}\label{11} \]

The complex conjugate of a number \(\ \underline{z}=x+j y\) is given by:

\[\ z^{*}=x-j y\label{12} \]

The sum of a complex number and its conjugate is real:

\[\ \underline{z}+\underline{z}^{*}=2 \operatorname{Re}(\underline{z})=2 x\label{13} \]

while the difference is imaginary:

\[\ \underline{z}-\underline{z}^{*}=2 j \operatorname{Im}(\underline{z})=2 j y\label{14} \]

where we have used the two symbols \(\ {Re}(\cdot)\) and \(\ {Im}(\cdot)\) to represent the operators which extract the real and imaginary parts of the complex number.

The complex conjugate of a complex number \(\ \underline{z}=|\underline{z}| e^{j \phi}\) may also be written as:

\[\ \underline{z}^{*}=|\underline{z}| e^{-j \phi}\label{15} \]

so that the product of a complex number and its conjugate is real:

\[\ \underline{z z}^{*}=|\underline{z}| e^{j \phi}|\underline{z}| e^{-j \phi}=|\underline{z}|^{2}\label{16} \]