2.2: Complex Exponential Notation
- Page ID
- 55516
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Start by recognizing a geometric interpretation for a complex number. If we plot the real part on the horizontal (x) axis and the imaginary part on the vertical (y) axis, then the complex number \(\ \underline{z}=x+j y\) (where \(\ j=\sqrt{-1}\)) represents a vector as shown in Figure 1. Note that this vector may be represented not only by its real and imaginary components, but also by a magnitude and a phase angle:
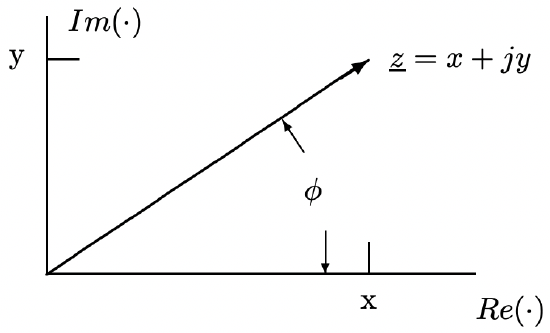Figure 1: Representation of the complex number \(\ \underline{z}=x+j y\)
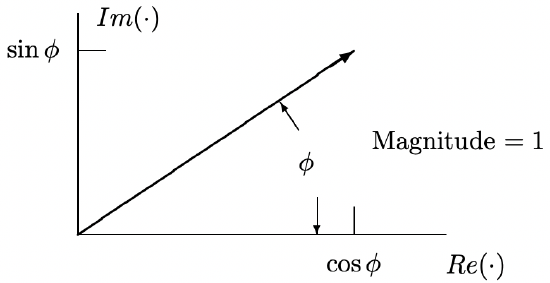Figure 2: Representation of \(\ e^{j \phi}\)\[\ |\underline{z}|=\sqrt{x^{2}+y^{2}}\label{1} \]
\[\ \phi=\arctan \left(\frac{y}{x}\right)\label{2} \]
The basis for complex exponential notation is the celebrated Euler Relation:
\[\ e^{j \phi}=\cos (\phi)+j \sin (\phi)\label{3} \]
which has a representation as shown in Figure 2.
Now, a comparison of Figures 1 and 2 makes it clear that, with definitions (1) and (2),
\[\ \underline{z}=x+j y=|\underline{z}| e^{j \phi}\label{4} \]
It is straightforward, using (3) to show that:
\[\ \cos (\phi)=\frac{e^{j \phi}+e^{-j \phi}}{2}\label{5} \]
\[\ \sin (\phi)=\frac{e^{j \phi}-e^{-j \phi}}{2 j}\label{6} \]
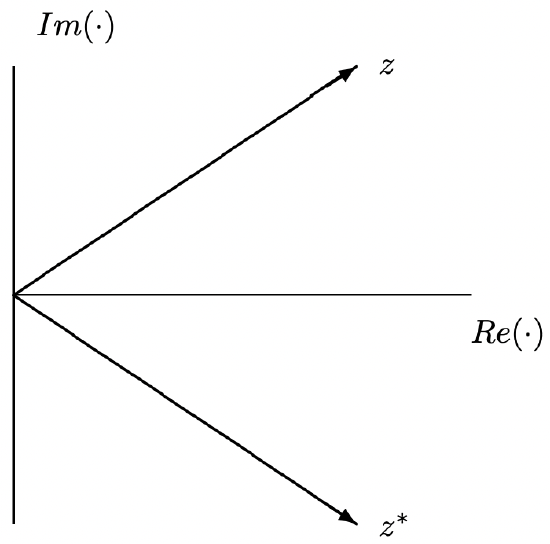Figure 3: Representation Of A Complex Number And Its ConjugateThe complex exponential is a tremendously useful type of function. Note that the product of two numbers expressed as exponenentials is the same as the exponential of the sums of the two exponents:
\[\ e^{a} e^{b}=e^{a+b}\label{8} \]
Note that it is also true that the reciprocal of a number in exponential notation is just the exponential of the negative of the exponent:
\[\ \frac{1}{e^{a}}=e^{-a}\label{9} \]
Then, if we have two numbers \(\ \underline{z}_{1}=\left|\underline{z}_{1}\right| e^{j \phi_{1}}\) and \(\ \underline{z}_{2}=\left|\underline{z}_{2}\right| e^{j \phi_{2}}\), then the product of the two numbers is:
\[\ \underline{z}_{1} \underline{z}_{2}=\left|\underline{z}_{1} \| \underline{z}_{2}\right| e^{j\left(\phi_{1}+\phi_{2}\right)}\label{10} \]
and the ratio of the two numbers is:
\[\ \frac{\underline{z}_{1}}{\underline{z}_{2}}=\frac{\left|\underline{z}_{1}\right|}{\left|\underline{z}_{2}\right|} e^{j\left(\phi_{1}-\phi_{2}\right)}\label{11} \]
The complex conjugate of a number \(\ \underline{z}=x+j y\) is given by:
\[\ z^{*}=x-j y\label{12} \]
The sum of a complex number and its conjugate is real:
\[\ \underline{z}+\underline{z}^{*}=2 \operatorname{Re}(\underline{z})=2 x\label{13} \]
while the difference is imaginary:
\[\ \underline{z}-\underline{z}^{*}=2 j \operatorname{Im}(\underline{z})=2 j y\label{14} \]
where we have used the two symbols \(\ {Re}(\cdot)\) and \(\ {Im}(\cdot)\) to represent the operators which extract the real and imaginary parts of the complex number.
The complex conjugate of a complex number \(\ \underline{z}=|\underline{z}| e^{j \phi}\) may also be written as:
\[\ \underline{z}^{*}=|\underline{z}| e^{-j \phi}\label{15} \]
so that the product of a complex number and its conjugate is real:
\[\ \underline{z z}^{*}=|\underline{z}| e^{j \phi}|\underline{z}| e^{-j \phi}=|\underline{z}|^{2}\label{16} \]