5.9: Transconductance

A field effect transistor is a voltage controlled current source. Its input is the gate potential, and the output is the source-drain current. In applications, we usually desire that the FET amplifies small changes in \(V_{GS}\). Thus, an important figure of merit for an FET is the transconductance, defined as

\[ g_{m} = \frac{dI_{ds}}{dV_{gs}} \nonumber \]

In the OFF state, the quantum capacitance is small and the gate‟s only influence on the FET is its electrostatic control of the channel potential. From Equation (5.3.1), we see that this control is maximized when

\[ C_{G} \gg C_{S},C_{D} \nonumber \]

This is an important design goal for FETs. Under this limit the transconductance is commonly expressed as:

\[ \frac{g_{m}}{I_{ds}} = \frac{1}{I_{ds}}\frac{dI_{ds}}{dV_{gs}} = \frac{q}{kT} \nonumber \]

Good electrostatic control of the channel may be achieved either by increasing the dielectric constant of the gate insulator, or by reducing the thickness of the gate insulator.

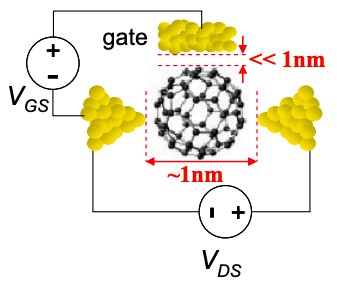
A good rule of thumb is that the gate must be much closer to the channel than either the source or drain contacts. Figure 5.9.1 shows the impact of varying \(C_{G}\) on our C60 molecular transistor. Increasing \(C_{G}\) shifts the switching gate voltage much lower.

Interestingly, to obtain this ideal characteristic, we increased \(C_{G}\) by three orders of magnitude relative to the more practical value used originally. This corresponds to increasing dielectric constant or reducing the gate-channel separation by three orders of magnitude.

Figure \(\PageIndex{1}\): A comparison of two C60 FETs. In (a) the gate has poor electrostatic control over the channel as evidenced by the small \(C_{G}\). In (b) the control is better, and the switching voltage is much lower.

For a molecular transistor with source-drain separation of a few nanometers, the gate insulator should be only a few Ångstroms – too thin to sufficiently insulate the gate. This represents a possibly insurmountable obstacle to 0-d channel devices such as single molecule FETs.

Figure \(\PageIndex{2}\): For high transconductance, the gate capacitance must be much higher than the source or drain channel capacitances. This forces impractically small gate-channel seperations in molecular transistors.

1d and 2d FETs

The central equation of conduction is

\[ I=\frac{q(N_{S}-N_{D})}{\tau} \nonumber \]

In 0-d the time constant, \(\tau\), was defined as the sum of the interfacial electron transfer time \(\tau_{S}\) and \(\tau_{D}\), which in turn can be thought of as representations of the interaction energy between the 0-d conductor and the source and drain contacts: \(\tau_{S}=\Gamma_{S}/\hbar\) and \(\tau_{D}=\Gamma_{D}/\hbar\), respectively.

Figure \(\PageIndex{3}\): (a) Electron transfer times in a 0-d conductor are related to the interaction energy \(\Gamma\) between the contact and the conductor. (b) In higher dimensions, we must determine the transit time from the electron velocity.

In higher dimensions, however, the electron transfer times at the contacts are less important. Rather, \(\tau\) is the transit time for an electron in the conductor. It is given by

\[ \tau=\frac{L_{x}}{v_{x}} \nonumber \]

where \(L_{x}\) is the length of the channel, and \(v_{x}\) is the velocity component of the electron parallel to the source-drain current. It is important to note that in 1-d, 2-d and 3-d conductors the transit time is dependent on the energy of the electron since the electron velocity, \(v_{x}\), is dependent on energy.

The other important change from the 0-d model concerns the density of states. In 0-d all states are accessible to electrons from both the source and drain contacts. But in higher dimensional ballistic devices, electrons injected from the source are only able to access states with momenta directed away from the source. We call these +k states. Similarly, the drain only injects electrons into –k states. Thus, we break the dispersion relation and density of states into two pieces, the density of +k states is given by \(g^{+}(E)dE\) and the density of –k states is given by \(g^{-}(E)dE\).

To summarize, in 1-d, 2-d and 3-d the fundamental equations for a transistor are:

\[ U_{ES} = -qV_{GS}\frac{C_{G}}{C_{ES}}-qV_{DS}\frac{C_{D}}{C_{ES}}+\frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber \]

\[ N=N_{S}+N_{D} \nonumber \]

\[ I=\frac{q}{\tau}(N_{S}-N_{D}) \nonumber \]

where

\[ N_{S} = \int^{\infty}_{-\infty} g^{+}(E-U)f(E, \mu_{S})dE \nonumber \]

\[ N_{D} = \int^{+\infty}_{-\infty} g^{-}(E-U)f(E, \mu_{D})dE \nonumber \]