6.3: Terminated Lines

Last updated
Save as PDF

Page ID: 88575

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

If, on the other hand, we have a finite line terminated with some load impedance, we have a somewhat more complicated problem to deal with, as shown in Figure $\PageIndex{1}$.

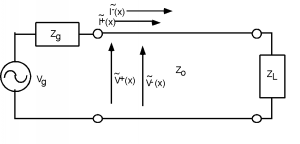
A transmission line of impedance z_0 has its left end connected to a sinusoidal voltage source v_g with source impedance z_g, and its right end connected to a load impedance z_L. There are voltages of tilde V+(x) and tilde V-(x) between the left endpoints of the transmission line, and currents of tilde I+(x) and I-(x) entering the transmission line from the source. — Figure $\PageIndex{1}$: A Finite Terminated Transmission Line

There are several things we should note before we head off into equation-land again. First of all, unlike the transient problems we looked at in a previous chapter, there can be no more than two voltage and current signals on the line, just $V^{+}$ and $V^{-}$ , (and $I^{+}$ and $I^{-}$ ). We no longer have the luxury of having $V_{1}^{+}$ , $V_{2}^{+}$ , etc., because we are talking now about a steady state system. All of the transient solutions which built up when the generator was first connected to the line have been summed together into just two waves.

Thus, on the line we have a single total voltage function, which is just the sum of the positive and negative going voltage waves

V (x) = V^{+} e^{- (i β x)} + V^{-} e^{i β x}

and a total current function

I (x) = I^{+} e^{- (i β x)} + I^{-} e^{i β x}

Note also that until we have solved for $V^{+}$ and $V^{-}$ , we do not know $V (x)$ or $I (x)$ anywhere on the line. In particular, we do not know $V (0)$ and $I (0)$ which would tell us what the apparent impedance is looking into the line.

\begin{array}{rcl} Z_{in} & = & Z (0) \\ = & \frac{V^{+} + V^{-}}{I^{+} + I^{-}} \end{array}

Until we know what kind of impedance the generator is seeing, we can not figure out how much of the generator's voltage will be coupled to the line! The input impedance looking into the line is now a function of the load impedance, the length of the line, and the phase velocity on the line. We have to solve this before we can figure out how the line and generator will interact.

The approach we shall have to take is the following. We will start at the load end of the line, and in a manner similar to the one we used previously, find a relationship between $V^{+}$ and $V^{-}$ , leaving their actual magnitude and phase as something to be determined later. We can then propagate the two voltages (and currents) back down to the input, determine what the input impedance is by finding the ratio of ( $V^{+} + V^{-}$ ) to ( $I^{+} + I^{-}$ ), and from this, and knowledge of properties of the generator and its impedance, determine what the actual voltages and currents are.

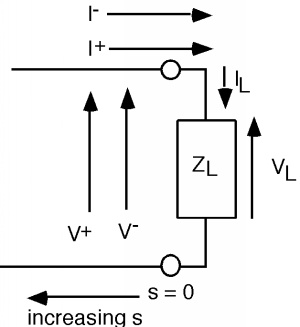
Let's take a look at the load. We again use KVL and KCL (Figure $\PageIndex{2}$) to match voltages and currents in the line and voltages and currents in the load:

V^{+} e^{- (i β L)} + V^{-} e^{i β L} = V_{L}

and

I^{+} e^{- (i β L)} + I^{-} e^{i β L} = I_{L}

The circuit from Figure 1 above has the left end of its transmission line labeled x=0, with x increasing towards the right, and the right end of its transmission line labeled s=0, with s increasing towards the left. The transmission line has length L. The voltage across the load impedance from bottom to top is V_L, the sum of V+ exp(j beta L) and V- exp(j beta L). The current entering the load impedance is I_L, the sum of I+ exp(j beta L) and I- exp(j beta L). — Figure $\PageIndex{2}$: Doing Kirchoff at the end of the line. Change variables!

Now, we could substitute $\frac{\pm (V)}{Z_{0}}$ for the two currents on the line and $\frac{V_{L}}{Z_{L}}$ for $I_{L}$ , and then try to solve for $V^{-}$ in terms of $V^{+}$ using Equation and Equation, but we can be a little clever at the outset and make our (complex) algebra a good bit cleaner, as shown in Figure $\PageIndex{3}$. Let's make a change of variable and let

s \equiv L - x

The right end of the circuit from Figure 2 above, where s=0. The exponential terms are gone, so I_L is the sum of I+ and I- and V_L is the sum of V+ and V-. — Figure $\PageIndex{3}$: $s=0$ at the load, and so the exponentials go away!

This then gives us for the voltage on the line (using $x = L - s$ )

V (s) = V^{+} e^{- (i β L)} e^{i β s} + V^{-} e^{i β L} e^{- (i β s)}

Usually, we just fold the (constant) phase terms $e^{\pm (i β L)}$ terms in with the $V^{+}$ and $V^{-}$ and so we have:

V (s) = V^{+} e^{i β s} + V^{-} e^{- (i β s)}

Note that when we do this, we now have a positive exponential in the first term associated with $V^{+}$ and a negative exponential associated with the $V^{-}$ term. Of course, we also get for $I (s)$ :

I (s) = I^{+} e^{i β s} + I^{-} e^{- (i β s)}

This change now moves our origin to the load end of the line, and reverses the direction of positive motion. But, now when we plug into $e^{i β s}$ the value for $s$ at the load ( $s = 0$ ), the equations simplify to:

V^{+} + V^{-} = V_{L}

and

I^{+} + I^{-} = I_{L}

which we then re-write as

\frac{V^{+}}{Z_{0}} - \frac{V^{-}}{Z_{0}} = \frac{V_{L}}{Z_{L}}

This is beginning to look almost exactly like a previous chapter. As a reminder, we solve Equation for $V_{L}$

V_{L} = \frac{Z_{L}}{Z_{0}} (V^{+} - V^{-})

and substitute for $V_{L}$ in Equation

V^{+} + V^{-} = \frac{Z_{L}}{Z_{0}} (V^{+} - V^{-})

From which we then solve for the reflection coefficient $Γ_{ν}$ , the ratio of $V^{-}$ to $V^{+}$ .

\frac{V^{-}}{V^{+}} \equiv Γ_{ν} = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}}

Note that since, in general, $Z_{L}$ will be complex, we can expect that $Γ_{ν}$ will also be a complex number with both a magnitude $| Γ_{ν} |$ and a phase angle $θ_{Γ}$ . Also, as with the case when we were looking at transients, $| Γ_{ν} | < 1$ .

Since we now know $V^{-}$ in terms of $V^{+}$ , we can now write an expression for $V (s)$ the voltage anywhere on the line.

V (s) = V^{+} e^{i β s} + V^{-} e^{- (i β s)}

Note again the change in signs in the two exponentials. Since our spatial variable $s$ is going in the opposite direction from $x$ , the $V^{+}$ phasor now goes as $i β s$ and the $V^{-}$ phasor now goes as $- (i β s)$ .

We now substitute in $Γ_{ν} V^{+}$ for $V^{-}$ in Equation, and for reasons that will become apparent soon, factor out an $e^{i β s}$ .

\begin{array}{rcl} V (s) & = & V^{+} e^{i β s} + Γ_{ν} V^{+} e^{- (i β s)} \\ = & V^{+} (e^{i β s} + Γ_{ν} e^{- (i β s)}) \\ = & V^{+} e^{i β s} (1 + Γ_{ν} e^{- (2 i β s)}) \end{array}

We could have also written down an equation for $I (s)$ , the current along the line. It will be a good test of your understanding of the basic equations we are developing here to show yourself that indeed

I (s) = \frac{V^{+} e^{i β s}}{Z_{0}} (1 - Γ_{ν} e^{- (2 i β s)})