6.5: Crank Diagram

Last updated
Save as PDF

Page ID: 88577

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We actually still have some options open to us. One of the nicest, at least in terms of getting some insight, is called a crank diagram. Note that this equation is a complex equation, which requires us to take the ratio of two complex numbers: $1 + Γ_{ν} e^{- (i 2 β s)}$ and $1 - Γ_{ν} e^{- (i 2 β s)}$ .

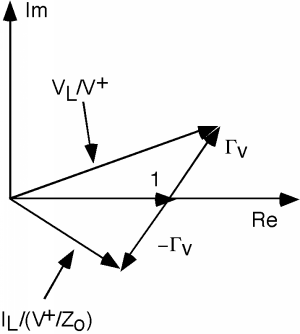
Let's plot these two quantities on the complex plane, starting at $s = 0$ (the load end of the line). We can represent $Γ_{ν}$ , the reflection coefficient, by its magnitude and its phase, which are $| Γ_{ν} |$ and $φ_{Γ}$ . For the numerator we plot a 1, and then add the complex vector $Γ$ which has a length $| Γ |$ and sits at an angle $φ_{Γ}$ with respect to the real axis, as shown in Figure $\PageIndex{1}$. The denominator is just the same thing, except that the $\Gamma$ vector points in the opposite direction as shown in Figure $\PageIndex{2}$.

First-quadrant graph with real components represented on the horizontal axis and imaginary components represented on the vertical axis. The vector representing 1 + Gamma_v extends up and to the right from the origin. The vector representing Gamma_v, with the magnitude of Gamma_v, extends up and to the right from the value of 1 on the real axis, at an angle of theta_Gamma from the real axis. The two vectors intersect at their heads. — Figure $\PageIndex{1}$: Plotting $1 + Γ_{ν}$

A plot with real components represented by the x-axis and imaginary components represented by the y-axis. A vector 1 - Gamma_v extends downwards and to the right from the origin. A vector representing Gamma_v, with the magnitude of Gamma_v, extends downwards and to the left, starting at the same point as the vector for Gamma_v from Figure 1 above but heading in the opposite direction. The two vectors intersect at their heads. — Figure $\PageIndex{2}$: Plotting $1 - Γ_{ν}$

The top vector is proportional to $V (s)$ and the bottom vector is proportional to $I (s)$ Figure $\PageIndex{3}$. Of course, for $s = 0$ we are at the load, so $V (s = 0) = V_{L}$ and $I (s = 0) = I_{L}$ .

The two plots from Figures 1 and 2 above are depicted on a single set of axes. The vector previously labeled 1 + Gamma_v now represents V_L / V+, and the vector previously labeled 1 - Gamma_v now represents I_L/(V+ / Z_0). — Figure $\PageIndex{3}$: Another crank diagram showing that $1 + Γ_{ν} = \frac{V_{L}}{V^{+}}$ and $1 - Γ_{ν} = \frac{Z_{0} I_{L}}{V^{+}}$

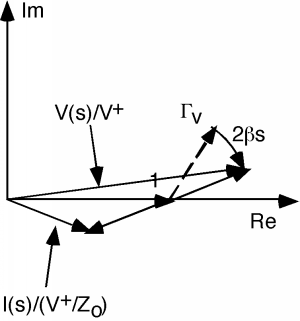
As we move down the line, the two " $Γ$ " vectors rotate around at a rate of $-2 β s$ as shown in Figure $\PageIndex{4}$. As they rotate, one vector gets longer and the other gets shorter, and then the opposite occurs. In any event, to get $Z (s)$ we have to divide the first vector by the second. In general, this is not easy to do, but there are some places where it is not too bad. One of these is when $2 β s = - θ_{Γ}$ , which is shown in Figure $\PageIndex{5}$.

The system of vectors from Figure 3 above is rotated a small amount clockwise so that the angle of the Gamma_v with respect to the real axis is decreased, with the rotation rate equal to 2 beta s. All contacts between heads and tails of the vectors and the vectors' points of contact with the axes that were present in Figure 3 are maintained here. — Figure $\PageIndex{4}$: Rotating the phasors on the crank diagram

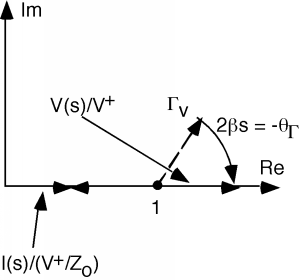
Continuation of the rotation of the crank diagram from Figure 4 above, so that all four vectors lie flat on the real axis. The value of 2 beta s is equal to -theta_Gamma. — Figure $\PageIndex{5}$: Rotating a crank diagram to a $V_{\max}$

At this point, the voltage vector has rotated around so that it is just lying on the real axis. Obviously its length is now $1 + | Γ |$ . By the same token, the current vector is also lying on the real axis, and has a length $1 - | Γ |$ . Dividing one by the other, and multiplying by $Z_{0}$ gives us $Z (s)$ at this point.

Z (s) = Z_{0} \frac{1 + | Γ_{ν} |}{1 - | Γ_{ν} |}

Where is this point, and does it have any special meaning? For this, we need to go back to our expression for $V (s)$ in this equation.

\begin{array}{rcl} V (s) & = & V^{+} e^{i β s} (1 + Γ_{ν} e^{-2 i β s}) \\ = & V^{+} e^{i β s} (1 + | Γ_{ν} | e^{i (θ_{Γ} - 2 β s)}) \\ = & V^{+} e^{i β s} (1 + | Γ_{ν} | e^{i φ (s)}) \end{array}

where we have substituted $| Γ_{ν} | e^{i θ}$ for the phasor $Γ_{ν}$ and then defined a new angle $φ (s) = θ_{Γ} - 2 β s$ .

Now let's find the magnitude of $V (s)$ . To do this we need to square the real and imaginary parts, add them, and then take the square root.

\begin{array}{rcl} | V (s) | & = & | V^{+} | (1 + | Γ_{ν} | e^{i φ (s)}) \\ = & | V^{+} | \sqrt{{(1 + | Γ_{ν} | \cos (φ (s)))}^{2} + {(| Γ_{ν} |)}^{2} \sin^{2} (φ (s))} \end{array}

so,

| V (s) | = | V^{+} | \sqrt{1 + 2 | Γ_{ν} | \cos (φ (s)) + {(| Γ_{ν} |)}^{2} \cos^{2} (φ (s)) + {(| Γ_{ν} |)}^{2} \sin^{2} (φ (s))}

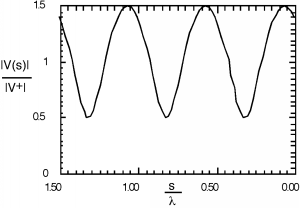
which, since $\sin^{2} (\cdot) + \cos^{2} (\cdot) = 1$

| V (s) | = | V^{+} | \sqrt{1 + {(| Γ_{ν} |)}^{2} + 2 | Γ_{ν} | \cos (φ (s))}

Remember, $φ (s)$ is an angle which changes with $s$ . In particular, $φ (s) = θ_{Γ} - 2 β s$ . Thus, as we move down the line $| V (s) |$ will oscillate as $\cos (φ (s))$ oscillates. A typical plot for $V (s)$ (for $| Γ_{ν} | = 0.5$ and $θ_{Γ} = 45^{°}$ ) is shown below in Figure $\PageIndex{6}$.

Plot of the standing wave pattern of the magnitude of V(s) divided by the magnitude of V+, over a horizontal axis of s divided by lambda. — Figure $\PageIndex{6}$: Standing wave pattern

Search

Text Color

Text Size

Margin Size

Font Type