6.12: Finding ZL

Last updated
Save as PDF

Page ID: 88584

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Let's move on to some other Smith Chart applications. Suppose, somehow, we can obtain a plot of $V (s)$ on a line with some unknown load on it. The data might look like Figure $\PageIndex{1}$. What can we tell from this plot? Well, $V (\max) = 1.7$ and $V (\min) = 0.3$ which means \[\begin{array}{l} \text{VSWR} &=& \frac{1.7}{0.3} \\ &=& 5.667 \end{array}\]

and hence

\begin{array}{rcl} | Γ | & = & \frac{VSWR - 1}{VSWR + 1} \\ = & \frac{4.667}{6.667} \\ = & 0.7 \end{array}

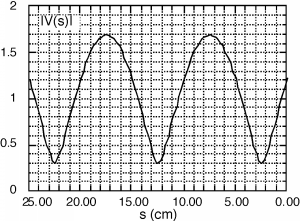
A standing wave pattern of V(s) with period 10 cm, maximum height 1.7, and minimum height 0.3.

Since $| r (s) | = | Γ |$ , we can plot $r (s)$ on the Smith Chart, as shown below in Figure $\PageIndex{2}$. We do this by setting the compass at a radius of 0.7 and drawing a circle! Now, $\frac{Z_{L}}{Z_{0}}$ is somewhere on this circle. We just do not know where yet! There is more information to be gleaned from the VSWR plot, however.

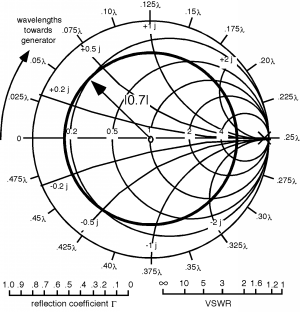
The mini Smith Chart with a circle of radius 0.7 superimposed on it, centered on the Smith Chart's leftmost point of the circle representing the real value of 1.

Firstly, we note that the plot has a periodicity of about 10 cm. This means that λ the wavelength of the signal on the line is 20 cm. Why? According to Equation 6.5.12, $| V (s) |$ goes as $\cos (φ (s))$ and $φ (s) = θ_{Γ} - 2 β s$ and $β = \frac{2 π}{λ}$ , thus $| V (s) |$ goes as $\cos (\frac{4 π s}{λ})$ . Thus each $\frac{\lambda}{2}$, we are back to where we started.

Secondly, we note that there is a voltage minima at about 2.5 cm away from the load. Where on Figure $\PageIndex{2}$ would we expect to find a voltage minima? It would be where $r (s)$ has a phase angle of $180^{°}$ or point "A" shown in Figure $\PageIndex{3}$. The voltage minima is always where the VSWR circle passes through the real axis on the left hand side. (Conversely a voltage maxima is where the circle goes through the real axis on the right hand side.) We don't really care about $\frac{Z (s)}{Z_{0}}$ at a voltage minima, what we want is $\frac{Z (s = 0)}{Z_{0}}$ , the normalized load impedance. This should be easy! If we start at "A" and go $\frac{2.5}{20} = 0.125 λ$ towards the load we should end up at the point corresponding to $\frac{Z_{L}}{Z_{0}}$ . The arrow on the mini-Smith Chart says "Wavelengths towards generator" If we start at A, and want to go towards the load, we had better go around the opposite direction from the arrow. (Actually, as you can see on a real Smith Chart, there are arrows pointing in both directions, and they are appropriately marked for your convenience.)

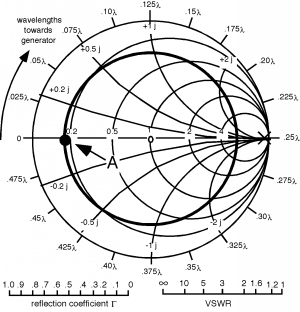
The VSWR circle on the mini Smith Chart from Figure 2 above has its minimum voltage point, where its leftmost point meets the horizontal axis, marked as point A.

So we start at "A" go $0.125 λ$ in a counterclockwise direction, and mark a new point "B" which represents our $\frac{Z_{L}}{Z_{0}}$ , which appears to be about $0.35 + -0.95 i$ or so, as in Figure $\PageIndex{4}$. Thus, the load in this case (assuming a $50 \text{-}\Omega$ line impedance) is a resistor, again by co-incidence of about $50 \ \Omega$, in series with a capacitor with a negative reactance of about $47.5 \ \Omega$. Note that we could have started at the minima at 12.5 cm or even 22.5 cm, and then have rotated $\frac{12.5}{20} = 0.625 λ$ or $\frac{22.5}{20} = 1.125 λ$ towards the load. Since $\frac{\lambda}{2} = 0.5 \lambda$ means one complete rotation around the Smith Chart, we would have ended up at the same spot, with the same $\frac{Z_{L}}{Z_{0}}$ that we already have! We could also have started at a maxima, at say 7.5 cm, marked our starting point on the right hand side of the Smith chart, and then we would go $0.375 λ$ counterclockwise and again, we'd end up at "B".

Figure 3 above is repeated with the point Z_L/Z_0, or the intersection of the lowest point on the VSWR circle with the main vertical axis labeled as B. A series of arrows points counterclockwise along the VSWR circle, going from point A to point B.

Now, here in Figure $\PageIndex{5}$ is another example. In this case the $VSWR = \frac{1.5}{0.5} = 3$ , which means $| Γ | = 0.5$ and we get a circle as shown in Figure $\PageIndex{6}$. The wavelength $λ = 2 \times (25 - 10) = 30 cm$ . The first minima is thus a distance of $\frac{10}{30} = 0.333 λ$ from the load. So we again start at the minima, "A" and now rotate as distance $0.333 λ$ towards the load.

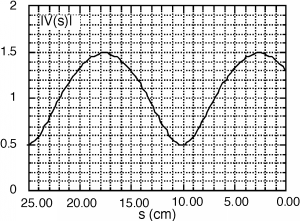
Standing wave pattern of V(s) with a period of 15 cm, maximum height of 1.5, and minimum height of 0.5.

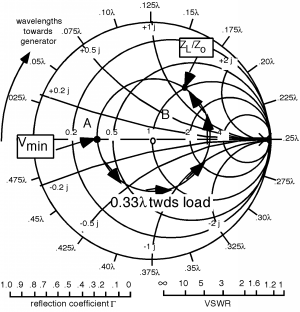
A VSWR circle of radius 0.5 is centered on a mini Smith Chart. The VSWR circle's leftmost point intersects with the horizontal axis at point A, the V_min, and Z_L/Z_0, the point where the VSWR circle intersects the Smith Chart circle representing a real value of 1 is labeled as point B. There is a distance of 0.33 lambda to travel counterclockwise along the VSWR circle from point A to point B.B.

Search

Text Color

Text Size

Margin Size

Font Type