4.7: Multimoding Considerations for Coplanar Waveguide
- Page ID
- 41046
The field orientation on CPW is little affected when frequency increases and as such the effective permittivity of CPW has little frequency dependence. (This is in marked contrast to microstrip. )Thus dielectric-related dispersion of CPW is minimal and this is one of the main advantages of using CPW over microstrip. CPW has the frequency-dependent line resistance
\[\label{eq:1}R(f)=\left\{\begin{array}{ll}{R(0)}&{f\text{ such that }t\leq 3\delta_{s}}\\{R(0)+R_{\text{skin}}(f)}&{f\text{ such that }t>3\delta_{s}}\end{array}\right. \]
where \(R(0) (= R_{\text{strip}}(0) + R_{\text{ground}}(0))\) is the resistance of the line at low frequencies. \(R(f)\) describes the frequency-dependent line resistance, which is due to both the skin effect and current bunching. Approximately,
\[\label{eq:2}R_{\text{skin}}(f)=R(0)k\sqrt{f} \]
where \(k\) is a constant. As with microstrip, EM simulations are recommended to determine line loss. This is necessary in any case to determine attenuation due to radiation, which can be ignored at low microwave frequencies.
The discussion of multimoding on CPW will consider the finite ground CPW structure (FGCPW) shown in Figure \(\PageIndex{1}\). Most of the considerations pertaining to multimoding on microstrip apply to FGCPW. However, with CPW the fields penetrate into the substrate a lesser distance and so it is less likely that the substrate mode or microstrip mode will be excited. To avoid the microstrip mode the FGCPW should be a sufficient distance from the bottom ground plane. Generally a substrate height three or more times both the gap and strip width is sufficient. A mode that can exist on FGCPW that does not have an equivalent with microstrip occurs when the ground strips on either side of the center strip acquire different voltages. The correct functioning of FGCPW requires these to be at the same potential. The solution is to connect the two side strips together using grounding straps as shown in Figure \(\PageIndex{2}\)(a). The straps are realized using bond wires if FGCPW is used on a circuit board, or using air bridges if the line is on a monolithic integrated circuit. Placing the strips at approximately one-quarter wavelength distances is appropriate, although this can be relaxed if the line
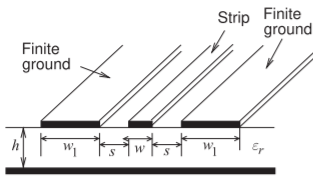
Figure \(\PageIndex{1}\): Finite ground CPW transmission line.
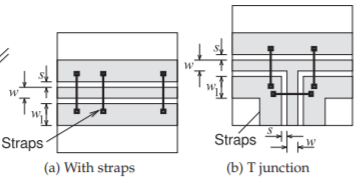
Figure \(\PageIndex{2}\): CPW structures with ground straps to suppress the parallel plate mode.

Figure \(\PageIndex{3}\): Stripline transmission line.
is fairly free of discontinuities. The straps should be placed randomly to avoid any filtering effect that could result from placing the straps at regular intervals. The straps should also be used whenever there is a discontinuity (see, e.g., the junction in Figure \(\PageIndex{2}\)(b)).


