4.7: Matrices
- Page ID
- 10115
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The word matrix dates at least to the thirteenth century, when it was used to describe the rectangular copper tray, or matrix, that held individual leaden letters that were packed into the matrix to form a page of composed text. Each letter in the matrix, call it \(a_{ij}\), occupied a unique position (ij) in the matrix. In modern day mathematical parlance, a matrix is a collection of numbers arranged in a two-dimensional array (a rectangle). We indicate a matrix with a boldfaced capital letter and the constituent elements with double subscripts for the row and column:

In this equation \(A\) is an \(mxn\) matrix, meaning that \(A\) has \(m\) horizontal rows and \(n\) vertical columns. As an extension of the previously used notation, we write \(A∈R^{mxn}\) to show that A is a matrix of size mxn with \(a_{ij}∈R\). The scalar element \(a_{ij}\) is located in the matrix at the ith row and the jth column. For example, a23 is located in the second row and the third column as illustrated in the Figure.
The main diagonal of any matrix consists of the elements aii. (The two subscripts are equal.) The main diagonal runs southeast from the top left corner of the matrix, but it does not end in the lower right corner unless the matrix is square (\(∈R^{m×m}\)).
The transpose of a matrix \(A∈R^{m×n}\) is another matrix \(B\) whose element in row j and column i is \(b_{ji}=a_{ij}\) for \(1≤i≤m\) and \(1≤j≤n\). We write \(B=A^T\) to indicate that \(B\) is the transpose of \(A\). In MATLAB, transpose is denoted by A'. A more intuitive way of describing the transpose operation is to say that it flips the matrix about its main diagonal so that rows become columns and columns become rows.
Exercise \(\PageIndex{1}\)
If \(A∈R^{m×n}\), then \(A^T∈?\). Find the transpose of the matrix \(A=\begin{bmatrix}2&5\\7&1\\4&9\end{bmatrix}\).
Matrix Addition and Scalar Multiplication
Two matrices of the same size (in both dimensions) may be added or subtracted in the same way as vectors, by adding or subtracting the corresponding elements. The equation \(C=A±B\) means that for each \(i\) and \(j,c_{ij}=a_{ij}±b_{ij}\). Scalar multiplication of a matrix multiplies each element of the matrix by the scalar:
\[aX=\begin{bmatrix} ax_{11} & ax_{12} & ax_{13} & ... & ax_{1n}\\ ax_{21} & ax_{22} & ax_{23} & ... & ax_{2n}\\ ax_{31} & ax_{32} & ax_{33} & ... & ax_{3n}\\ ⠇& ⠇ & ⠇& & ⠇\\ ax_{m1} & ax_{m2} & ax_{m3} & ... & ax_{mn} \end{bmatrix} \nonumber \]
Matrix Multiplication
A vector can be considered a matrix with only one column. Thus we intentionally blur the distinction between \(R^{n×1}\) and \(R^n\). Also a matrix can be viewed as a collection of vectors, each column of the matrix being a vector:
\[\mathrm{A}=\left[\begin{array}{llll}
\mid & \mid & & 1 \\
\mathrm{a}_{1} & \mathrm{a}_{2} & \ldots & \mathrm{a}_{n} \\
\mid & \mid & & \mid
\end{array}\right]=\left[\left[\begin{array}{l}
a_{11} \\
a_{21} \\
\mid \\
a_{m 1}
\end{array}\right]\left[\begin{array}{l}
a_{12} \\
a_{22} \\
\mid \\
a_{m 2}
\end{array}\right]\left[\begin{array}{l}
a_{1 n} \\
a_{2 n} \\
\mid \\
a_{m n}
\end{array}\right]\right] \nonumber \]
In the transpose operation, columns become rows and vice versa. The transpose of an \(n×1\) matrix, a column vector, is a 1 ×\(n\) matrix, a row vector:
\[\mathrm{x}=\left[\begin{array}{l}
x_{1} \\
x_{2} \\
\mid \\
x_{n}
\end{array}\right] ; \mathrm{x}^{T}=\left[x_{1} x_{2} x_{n}\right] \nonumber \]
Now we can define matrix-matrix multiplication in terms of inner products of vectors. Let's begin with matrices \(\mathrm{A} \in \mathscr{R}^{m \times n}\) and \(\mathrm{B} \in \mathscr{R}^{n \times p}\). To find the product AB, first divide each matrix into column vectors and row vectors as follows:
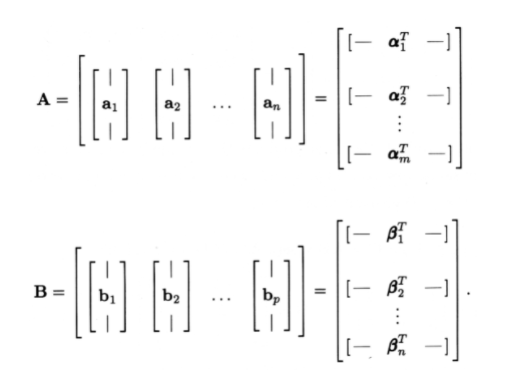
Thus \(a_i\) is the \(i^{th}\) column of A and \(α^T_j\) is the \(j^{th}\) row of A. For matrix multiplication to be defined, the width of the first matrix must match the length of the second one so that all rows \(α^T_i\) and columns \(b_i\) have the same number of elements \(n\). The matrix product, C=AB, is an \(m×p\) matrix defined by its elements as \(c_{ij}\)=\((α_i,b_j)\). In words, each element of the product matrix, \(c_{ij}\), is the inner product of the \(i^{th}\) row of the first matrix and the \(j^{th}\) column of the second matrix.
For n-vectors \(x\) and \(y\), the matrix product \(x^Ty\) takes on a special significance. The product is, of course, a 1×1 matrix (a scalar). The special significance is that \(x^Ty\) is the inner product of \(x\) and \(y\):

Thus the notation \(x^Ty\) is often used in place of (x,y). Recall from Demo 1 from "Linear Algebra: Other Norms" that MATLAB uses x'*y to denote inner product.
Another special case of matrix multiplication is the outer product. Like the inner product, it involves two vectors, but this time the result is a matrix:
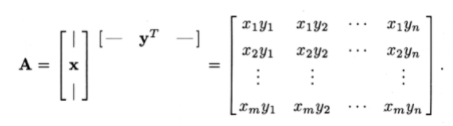
In the outer product, the inner products that define its elements are between one-dimensional row vectors of \(x\) and one-dimensional column vectors of \(y^T\), meaning the \((i,j)\) element of \(A\) is \(x_iy_j\).
Find \(C=AB\) where \(A\) and \(B\) are given by
- \(A=\left[\begin{array}{lll}
1 & -1 & 2 \\
3 & 0 & 5
\end{array}\right]\) ; \(B=\left[\begin{array}{llll}
0 & -2 & 1 & -3 \\
4 & 2 & 2 & 0 \\
2 & -2 & 3 & 1
\end{array}\right]\); - \(A=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) ; \(B=\left[\begin{array}{llll}
1 & 2 & 3 & 4 \\
5 & 6 & 7 & 8
\end{array}\right]\); - \(\mathrm{A}=\left[\begin{array}{ccc}
1 & -1 & -1 \\
1 & -1 & 1 \\
1 & 1 & 1
\end{array}\right]\) ; \(B=\left[\begin{array}{lll}
0 & 3 & 6 \\
1 & 4 & 7 \\
2 & 5 & 8
\end{array}\right]\)
There are several other equivalent ways to define matrix multiplication, and a careful study of the following discussion should improve your understanding of matrix multiplication. Consider \(\mathrm{A} \in \mathscr{R}^{m \times n}\),\(\mathbf{B} \in \mathscr{R}^{n \times p}\), and C=AB so that \(\mathrm{C} \in \mathscr{R}^{m \times p}\). In pictures, we have
\[m\left[\begin{array}{l}
p \\
\mathrm{C}
\end{array}\right]=m\left[\begin{array}{l}
n \\
\mathrm{~A}
\end{array}\right]\left[\begin{array}{l}
p \\
\mathrm{~B}
\end{array}\right] n \nonumber \]
In our definition, we represent \(C\) on an entry-by-entry basis as
\[\mathrm{c}_{i j}=\left(\alpha_{i}, \mathrm{~b}_{j}\right)=\sum_{k=1}^{n} \mathrm{a}_{i k} b_{k j} \nonumber \]
In pictures,
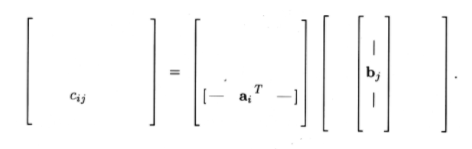
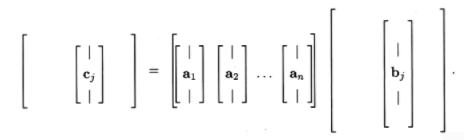
You will prove in Exercise 3 that we can also represent \(C\) on a column basis:
\[\mathrm{c}_{j}=\sum_{k=1}^{n} \mathrm{a}_{k} b_{k j} \nonumber \]
Finally, \(C\) can be represented as a sum of matrices, each matrix being an outer product:
\[\mathrm{C}=\sum_{i=1}^{n} \mathrm{a}_{i} \beta_{i}^{T} \nonumber \]
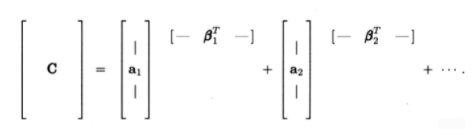
A numerical example should help clarify these three methods.
Let
\(A=\left[\begin{array}{llll}
1 & 2 & 1 & 3 \\
2 & 1 & 2 & 4 \\
3 & 3 & 2 & 1
\end{array}\right], \quad B=\left[\begin{array}{lll}
1 & 2 & 1 \\
2 & 2 & 1 \\
1 & 3 & 2 \\
2 & 1 & 1
\end{array}\right] \text { . }\)
Using the first method of matrix multiplication, on an entry-by-entry basis, we have
\(\mathrm{c}_{i j}=\sum_{k=1}^{4} \mathrm{a}_{i k} b_{k j}\)
or
\(\mathrm{C}=\left[\begin{array}{lll}
(1 \cdot 1+2 \cdot 2+1 \cdot 1+3 \cdot 2) & (1 \cdot 2+2 \cdot 2+1 \cdot 3+3 \cdot 1) & (1 \cdot 1+2 \cdot 1+1 \cdot 2+3 \cdot 1) \\
(2 \cdot 1+1 \cdot 2+2 \cdot 1+4 \cdot 2) & (2 \cdot 2+1 \cdot 2+2 \cdot 3+4 \cdot 1) & (2 \cdot 1+1 \cdot 1+2 \cdot 2+4.1) \\
(3 \cdot 1+3 \cdot 2+2 \cdot 1+1 \cdot 2) & (3 \cdot 2+3 \cdot 2+2 \cdot 3+1 \cdot 1) & (3 \cdot 1+3 \cdot 1+2 \cdot 2+1 \cdot 1)
\end{array}\right]\)
or
\(\mathrm{C}=\left[\begin{array}{ccc}
12 & 12 & 8 \\
14 & 16 & 11 \\
13 & 19 & 11
\end{array}\right]\)
On a column basis,
\(\mathrm{c}_{j}=\sum_{k=1}^{4} \mathrm{a}_{k} b_{k j}\)
\(\mathrm{c}_{1}=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right] 1+\left[\begin{array}{l}
2 \\
1 \\
3
\end{array}\right] 2+\left[\begin{array}{l}
1 \\
2 \\
2
\end{array}\right] 1+\left[\begin{array}{l}
3 \\
4 \\
1
\end{array}\right] 2 ; \mathrm{c}_{2}=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right] 2+\left[\begin{array}{l}
2 \\
1 \\
3
\end{array}\right] 2+\left[\begin{array}{l}
1 \\
2 \\
2
\end{array}\right] 3+\left[\begin{array}{l}
3 \\
4 \\
1
\end{array}\right] 1 ; c_{3}=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right] 1+\left[\begin{array}{l}
2 \\
1 \\
3
\end{array}\right] 1+\left[\begin{array}{l}
1 \\
2 \\
2
\end{array}\right] 2+\left[\begin{array}{l}
3 \\
4 \\
1
\end{array}\right] 1\)
Collecting terms together, we have
\(\begin{array}{c}
\mathrm{C}=\left[\mathrm{c}_{1} \mathrm{c}_{2} \mathrm{c}_{3}\right] \\
\mathrm{C}=\left[\begin{array}{cc}
(1 \cdot 1+2 \cdot 2+1 \cdot 1+3 \cdot 2) & (1 \cdot 2+2 \cdot 2+1 \cdot 3+3 \cdot 1) & (1 \cdot 1+2 \cdot 1+1 \cdot 2+3 \cdot 1) \\
(2 \cdot 1+1 \cdot 2+2 \cdot 1+4 \cdot 2) & (2 \cdot 2+1 \cdot 2+2 \cdot 3+4 \cdot 1) & (2 \cdot 1+1 \cdot 1+2 \cdot 2+4.1) \\
(3 \cdot 1+3 \cdot 2+2 \cdot 1+1 \cdot 2) & (3 \cdot 2+3 \cdot 2+2 \cdot 3+1 \cdot 1) & (3 \cdot 1+3 \cdot 1+2 \cdot 2+1 \cdot 1)
\end{array}\right]
\end{array}\)
On a matrix-by-matrix basis,
\(\mathrm{C}=\sum_{i=1}^{4} \mathrm{a}_{i} \beta_{i}^{T}\)
\(C=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 1
\end{array}\right]+\left[\begin{array}{l}
2 \\
1 \\
3
\end{array}\right]\left[\begin{array}{lll}
2 & 2 & 1
\end{array}\right]+\left[\begin{array}{lll}
1 & 3 & 2
\end{array}\right]+\left[\begin{array}{l}
1 \\
2 \\
2
\end{array}\right]\left[\begin{array}{lll}
1 & 3 & 2
\end{array}\right]+\left[\begin{array}{l}
3 \\
4 \\
1
\end{array}\right]\left[\begin{array}{lll}
1 & 1 & 1
\end{array}\right]\)
\(=\left[\begin{array}{lll}
1 \cdot 1 & 1 \cdot 2 & 1 \cdot 1 \\
2 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\
3 \cdot 1 & 3 \cdot 2 & 3 \cdot 1
\end{array}\right]+\left[\begin{array}{lll}
2 \cdot 2 & 2 \cdot 2 & 2 \cdot 1 \\
1 \cdot 2 & 1 \cdot 2 & 1 \cdot 1 \\
3 \cdot 2 & 3 \cdot 2 & 3 \cdot 1
\end{array}\right]+\left[\begin{array}{ccc}
1 \cdot 1 & 1 \cdot 3 & 1 \cdot 2 \\
2 \cdot 1 & 2 \cdot 3 & 2 \cdot 2 \\
2 \cdot 1 & 2 \cdot 3 & 2 \cdot 2
\end{array}\right]+\left[\begin{array}{ccc}
3 \cdot 2 & 3 \cdot 1 & 3 \cdot 1 \\
4 \cdot 2 & 4 \cdot 1 & 4 \cdot 1 \\
1 \cdot 2 & 1 \cdot 1 & 1 \cdot 1
\end{array}\right]\)
\(\mathrm{C}=\left[\begin{array}{lll}
(1 \cdot 1+2 \cdot 2+1 \cdot 1+3 \cdot 2) & (1 \cdot 2+2 \cdot 2+1 \cdot 3+3 \cdot 1) & (1 \cdot 1+2 \cdot 1+1 \cdot 2+3 \cdot 1) \\
(2 \cdot 1+1 \cdot 2+2 \cdot 1+4 \cdot 2) & (2 \cdot 2+1 \cdot 2+2 \cdot 3+4 \cdot 1) & (2 \cdot 1+1 \cdot 1+2 \cdot 2+4.1) \\
(3 \cdot 1+3 \cdot 2+2 \cdot 1+1 \cdot 2) & (3 \cdot 2+3 \cdot 2+2 \cdot 3+1 \cdot 1) & (3 \cdot 1+3 \cdot 1+2 \cdot 2+1 \cdot 1)
\end{array}\right]\)
as we had in each of the other cases. Thus we see that the methods are equivalent-simply different ways of organizing the same computation!
Prove that Equations 5, 6, and 7 are equivalent definitions of matrix multiplication. That is, if C=AB where \(\mathrm{A} \in \mathscr{R}^{m \times n}\) and \(\mathrm{B} \in \mathscr{R}^{n \times p}\), show that the matrix-matrix product can also be defined by
\(c_{i j}=\sum_{k=1}^{n} a_{i k} b_{k j}\)
and, if \(c_k\) is the \(k^{th}\) column of \(C\) and \(a_k\) is the \(k^{th}\) column of \(A\), then
\(\mathrm{c}_{j}=\sum_{k=1}^{n} \mathrm{a}_{k} b_{k j}\)
Show that the matrix \(C\) may also be written as the ‚ "sum of outer products"
\(\mathrm{C}=\sum_{k=1}^{n} \mathrm{a}_{k} \beta_{k}^{T}\)
Write out the elements in a typical outer product \(\mathrm{a}_{k} \beta_{k}^{T} \text { . }\)
Given \(\mathrm{A} \in \mathscr{R}^{m \times n}\),\(\mathrm{B} \in \mathscr{R}^{n \times p}\), and \(\mathrm{C} \in \mathscr{R}^{r \times s}\), for each of the following postulates, either prove that it is true or give a counterexample showing that it is false:
- \(\left(\mathrm{A}^{T}\right)^{T}=\mathrm{A}\)
- \(AB=BA\) when \(n=p\) and \(m=q\). Is matrix multiplication commutative?
- A(B+C)=AB+AC when \(n=p=r\) and \(q=s\). Is matrix multiplication distributive over addition?
- \((\mathrm{AB})^{T}=\mathrm{B}^{T} \mathrm{~A}^{T}\) when \(n=p\)
- (AB)C=A(BC) when \(n=p\) and \(q=r\). Is matrix multiplication associative?
Rotation
We know from the chapter on complex numbers that a complex number \(z_1=x_1+jy_1\) may be rotated by angle \(\theta\) in the complex plane by forming the product
\(z_{2}=e^{j \theta} z_{1}\)
When written out, the real and imaginary parts of \(z_2\) are
\(\begin{aligned}
z_{2} &=\qquad \qquad (\cos \theta+j \sin \theta)\left(x_{1}+j y_{1}\right) \\
&=(\cos \theta) x_{1}-(\sin \theta) y_{1}+j\left[(\sin \theta) x_{1}+(\cos \theta) y_{1}\right]
\end{aligned}\)
If the real and imaginary parts of \(z_1\) and \(z_2\) are organized into vectors \(z_1\) and \(z_2\) as in the chapter on complex numbers, then rotation may be carried out with the matrix-vector multiply
\(\mathrm{z}_{2}=\left[\begin{array}{l}
x_{2} \\
y_{2}
\end{array}\right]=\left[\begin{array}{ll}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\left[\begin{array}{l}
x_{1} \\
y_{1}
\end{array}\right]\)
We call the matrix \(\mathrm{R}(\theta)=\left[\begin{array}{ll}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\) a rotation matrix.
Let \(R(\theta)\)denote a 2×2 rotation matrix. Prove and interpret the following two properties:
- \(\mathrm{R}^{T}(\theta)=\mathrm{R}(-\theta)\);
- \(\mathrm{R}^{T}(\theta) \mathrm{R}(\theta)=\mathrm{R}(\theta) \mathrm{R}^{T}(\theta)=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)


