6.2.1: Gibbs Inequality

Here we present the Gibbs Inequality, named after the American physicist J. Willard Gibbs (1839–1903)\(^1\), which will be useful to us in later proofs. This inequality states that the entropy is smaller than or equal to any other average formed using the same probabilities but a different function in the logarithm. Specifically

\(\displaystyle \sum_{i} p(A_i)\log_2\Big(\dfrac{1}{p(A_i)}\Big) \leq \displaystyle \sum_{i} p(A_i)\log_2\Big(\dfrac{1}{p'(A_i)}\Big) \tag{6.4}\)

where \(p(A_i)\) is any probability distribution (we will use it for source events and other distributions) and \(p'(A_i)\) is any other probability distribution, or more generally any set of numbers such that

\(0 \leq p'(A_i) \leq 1 \tag{6.5}\)

and

\(\displaystyle \sum_{i} p'(A_i) \leq 1. \tag{6.6}\)

As is true for all probability distributions,

\(\displaystyle \sum_{i} p(A_i) = 1. \tag{6.7}\)

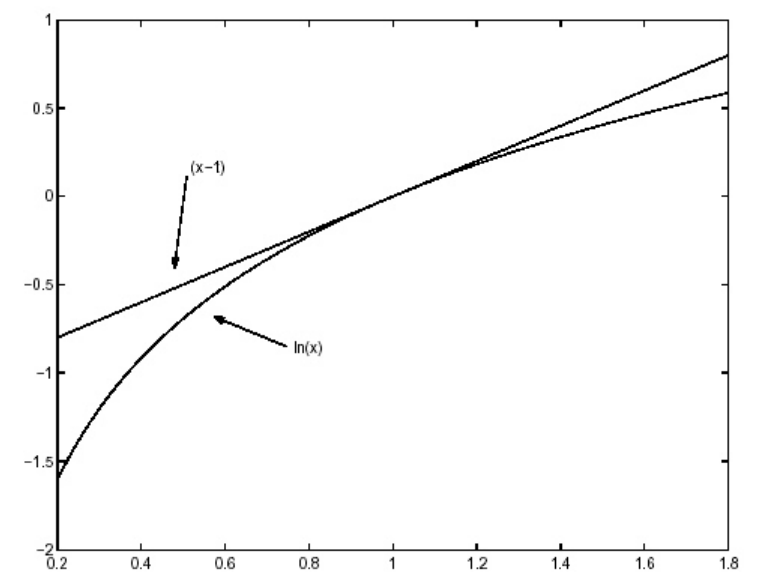
Equation 6.4 can be proven by noting that the natural logarithm has the property that it is less than or equal to a straight line that is tangent to it at any point, (for example the point \(x\) = 1 is shown in Figure 6.2). This property is sometimes referred to as concavity or convexity. Thus

and therefore, by converting the logarithm base \(e\) to the logarithm base 2, we have

Then

\[\begin{align*}
\displaystyle \sum_{i} p(A_i) \log_2 \Big(\dfrac{1}{p(A_i)}\Big) - \displaystyle \sum_{i} p(A_i) \log_2 \Big(\dfrac{1}{p'(A_i)}\Big) &= \displaystyle \sum_{i} p(A_i) \log_2 \Big(\dfrac{p'(A_i)}{p(A_i)}\Big) \\
&\leq \log_2 e \displaystyle \sum_{i} p(A_i) \begin{bmatrix} \dfrac{p'(A_i)}{p(A_i)} - 1 \end{bmatrix} \\
&= \log_2 e \Big(\displaystyle \sum_{i} p'(A_i) - \sum_{i} p(A_i)\Big) \\
&= \log_2 e \Big(\displaystyle \sum_{i} p'(A_i) - 1\Big) \\
&\leq 0 \tag{6.10}
\end{align*} \nonumber \]

Figure 6.2: Graph of the inequality \(\ln x ≤ (x − 1)\)

---

\(^1\)See a biography of Gibbs at http://www-groups.dcs.st-andrews.ac....ies/Gibbs.html