15.2: Vector Spaces

Introduction

Definition: Vector Space

A vector space \(S\) is a collection of "vectors" such that (1) if \(f_{1} \in S \Rightarrow \alpha f_{1} \in S\) for all scalars \(\alpha\) (where \(alpha \in \mathbb{R}\), \(\alpha \in \mathbb{C}\), or some other field) and (2) if \(f_{1} \in S\), \(f_2 \in S\), then \((f_1+f_2) \in S\)

To define an vector space, we need

• A set of things called "vectors" (\(X\))
• A set of things called "scalars" that form a field (\(A\))
• A vector addition operation ()
• A scalar multiplication operation (\(*\))

The operations need to have all the properties of given below. Closure is usually the most important to show.

Vector Spaces

If the scalars \(\alpha\) are real, \(S\) is called a real vector space.

If the scalars \(\alpha\) are complex, \(S\) is called a complex vector space.

If the "vectors" in \(S\) are functions of a continuous variable, we sometimes call \(S\) a linear function space

Properties

We define a set \(V\) to be a vector space if

1. \(x+y=y+x\) for each \(x\) and \(y\) in \(V\)
2. \(x+(y+z)=(x+y)+z\) for each \(x\), \(y\), and \(z\) in \(V\)
3. There is a unique "zero vector" such that \(x+0=x\) for each \(x\) in \(V\) (0 is the field additive identity)
4. For each \(x\) in \(V\) there is a unique vector \(−x\) such that \(x+−x=0\)
5. \(1x=x\) (1 is the field multiplicative identity)
6. \((c_1c_2)x=c_1(c_2x)\) for each \(x\) in \(V\) and \(c_1\) and \(c_2\) in \(\mathbb{C}\)
7. \(c(x+y)=cx+cy\) for each \(x\) and \(y\) in \(V\) and \(c\) in \(\mathbb{C}\)
8. \((c_1+c_2)x=c_1x+c_2x\) for each \(x\) in \(V\) and \(c_1\) and \(c_2\) in \(\mathbb{C}\)

Examples

• \(\mathbb{R}^n\) = real vector space
• \(\mathbb{C}^n\) = complex vector space
• \(L^{1}(\mathbb{R})=\left\{f(t), f(t) | \int_{-\infty}^{\infty}\left| f(t) \right| \mid d t<\infty\right\}\) is a vector space
• \(L^{\infty}(\mathbb{R})=\{f(t), f(t) \mid f(t) \text { is bounded }\}\) is a vector space
• \(L^{2}(\mathbb{R})=\left\{f(t), f(t) | \int_{-\infty}^{\infty}(|f(t)|)^{2} d t<\infty\right\}\) = finite energy signals is a vector space
• \(L^{2}([0, T])\) = finite energy functions on interval \([0,T]\)
• \(\ell^{1}(\mathbb{Z})\), \(\ell^{2}(\mathbb{Z})\), \(\ell^{\infty}(\mathbb{Z})\) are vector spaces
• The collection of functions piecewise constant between the integers is a vector space

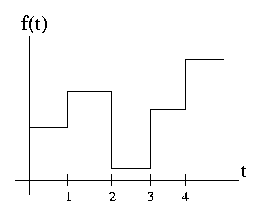
Figure \(\PageIndex{1}\)

• \(\mathbb{R}_{+}^{2}=\left\{\left(\begin{array}{l}
  x_{0} \\
  x_{1}
  \end{array}\right),\left(\begin{array}{l}
  x_{0} \\
  x_{1}
  \end{array}\right) \mid\left(x_{0}>0\right) \wedge\left(x_{1}>0\right)\right\}\) is not a vector space. \(\left(\begin{array}{l}
  1 \\
  1
  \end{array}\right) \in \mathbb{R}_{+}^{2}\), but \(\alpha\left(\begin{array}{l}
  1 \\
  1
  \end{array}\right) \notin \mathbb{R}_{+}^{2}\), \(\alpha < 0\)
• \(D=\left\{z \in \mathbb{C},|z| \leq 1\right\}\) is not a vector space. \(\left(z_{1}=1\right) \in D\), \((z_2=j) \in D\), but \(\left(z_{1}+z_{2}\right) \notin D\), \(\left|z_{1}+z_{2}\right|=\sqrt{2}>1\)

Note

Vector spaces can be collections of functions, collections of sequences, as well as collections of traditional vectors (i.e. finite lists of numbers)