15.3: Norms
- Page ID
- 22937
Introduction
This module will explain norms, a mathematical concept that provides a notion of the size of a vector. Specifically, the general definition of a norm will be discussed and discrete time signal norms will be presented.
Norms
The norm of a vector is a real number that represents the "size" of the vector.
Example \(\PageIndex{1}\)
In \(\mathbb{R}^2\), we can define a norm to be a vectors geometric length.
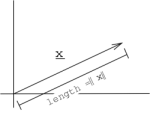
Figure \(\PageIndex{1}\)
\(\boldsymbol{x}=(x_0,x_1)^T\), norm \(\|\boldsymbol{x}\|=\sqrt{x_{0}^{2}+x_{1}^{2}}\)
Mathematically, a norm \(\|\cdot\|\) is just a function (taking a vector and returning a real number) that satisfies three rules.
To be a norm, \(\|\cdot\|\) must satisfy:
- the norm of every vector is positive \(\|x\|>0\), \(x \in S\)
- scaling a vector scales the norm by the same amount \(\|\alpha x\|=|\alpha|\|x\|\) for all vectors \(x\) and scalars \(\alpha\)
- Triangle Property: \(\|x+y\| \leq\|x\|+\|y\|\) for all vectors \(x\), \(y\). "The "size" of the sum of two vectors is less than or equal to the sum of their sizes"
A vector space (Section 15.2) with a well defined norm is called a normed vector space or normed linear space.
Examples
Example \(\PageIndex{2}\)
\(\mathbb{R}^n\) (or \(\mathbb{C}^n\)), \(\boldsymbol{x}=\left(\begin{array}{c}
x_{0} \\
x_{1} \\
\dots \\
x_{n-1}
\end{array}\right)\), \(\|x\|_{1}=\sum_{i=0}^{n-1}\left|x_{i}\right|\), \(\mathbb{R}^n\) with this norm is called \(\ell^{1}([0, n-1])\).
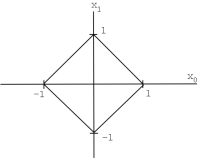
Example \(\PageIndex{3}\)
\(\mathbb{R}^n\) (or \(\mathbb{C}^n\)), with norm \(\|x\|_{2}=\left(\sum_{i=0}^{n-1}\left(\left|x_{i}\right|\right)^{2}\right)^{\frac{1}{2}}\), \(\mathbb{R}^n\) is called \(\ell^{2}([0, n-1])\) (the usual "Euclidean"norm).
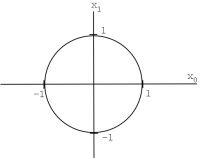
Example \(\PageIndex{4}\)
\(\mathbb{R}^n\) (or \(\mathbb{C}^n\)), with norm \(\|x\|_{\infty}=\max _{i}\left\{i,\left|x_{i}\right|\right\}\) is called \(\ell^{\infty}([0, n-1])\)
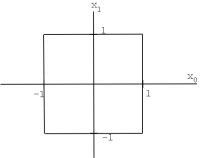
Spaces of Sequences and Functions
We can define similar norms for spaces of sequences and functions.
Discrete time signals = sequences of numbers
\[x[n]=\left\{\ldots, x_{-2}, x_{-1}, x_{0}, x_{1}, x_{2}, \ldots\right\} \nonumber \]
- \(\|x(n)\|_{1}=\sum_{i=-\infty}^{\infty}|x[i]|, x[n] \in \ell^{1}(\mathbb{Z}) \Rightarrow\left(\|x\|_{1}<\infty\right)\)
- \(\|x(n)\|_{2}=\left(\sum_{i=-\infty}^{\infty}(|x[i]|)^{2}\right)^{\frac{1}{2}}, x[n] \in \ell^{2}(\mathbb{Z}) \Rightarrow\left(\|x\|_{2}<\infty\right)\)
- \(\|x(n)\|_{p}=\left(\sum_{i=-\infty}^{\infty}(|x[i]|)^{P}\right)^{\frac{1}{p}}, x[n] \in \ell^{p}(\mathbb{Z}) \Rightarrow\left(\|x\|_{p}<\infty\right)\)
- \(\|x(n)\|_{\infty}=\sup _{i}|x[i]|, x[n] \in \ell^{\infty}(\mathbb{Z}) \Rightarrow\left(\|x\|_{\infty}<\infty\right)\)
For continuous time functions:
- \(\|f(t)\|_{p}=\left(\int_{-\infty}^{\infty}(|f(t)|)^{p} d t\right)^{\frac{1}{p}}, f(t) \in L^{p}(\mathbb{R}) \Rightarrow\left(\|f(t)\|_{p}<\infty\right)\)
- \(\|f(t)\|_{p}=\left(\int_{0}^{T}(|f(t)|)^{p} d t\right)^{\frac{1}{p}}, f(t) \in L^{p}([0, T]) \Rightarrow\left(\|f(t)\|_{p}<\infty\right)\)


