15.11: Haar Wavelet Basis
- Page ID
- 23201
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Fourier series is a useful orthonormal representation (Section 15.9) on \(L^2([0,T])\) especially for inputs into LTI systems. However, it is ill suited for some applications, i.e. image processing (recall Gibb's phenomena (Section 6.7)).
Wavelets, discovered in the last 15 years, are another kind of basis for \(L^2([0,T])\) and have many nice properties.
Basis Comparisons
Fourier series - \(c_n\) give frequency information. Basis functions last the entire interval.
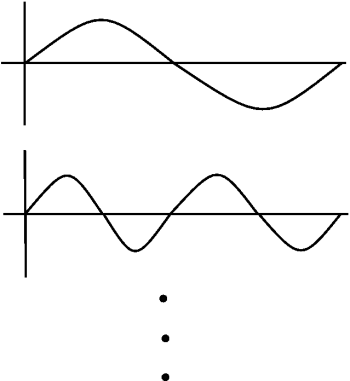
Wavelets - basis functions give frequency info but are local in time.
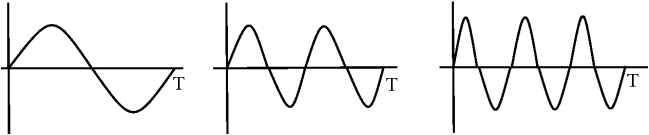
In Fourier basis, the basis functions are harmonic multiples of \(e^{j \omega_0 t}\)
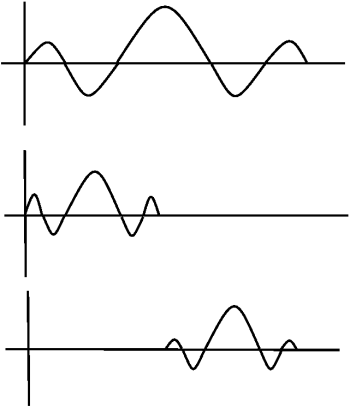
In Haar wavelet basis, the basis functions are scaled and translated versions of a "mother wavelet" \(\psi(t)\).
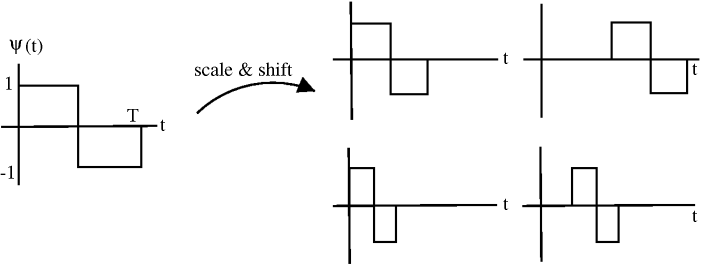
Figure \(\PageIndex{4}\)
Basis functions \(\left\{\psi_{j, k}(t)\right\}\) are indexed by a scale j and a shift k.
Let \(\phi(t)=1\), \(0 \leq t<T\) Then \(\left\{\phi(t), 2^{\frac{j}{2}} \psi\left(2^{j} t-k\right), \phi(t), 2^{\frac{j}{2}} \psi\left(2^{j} t-k\right) \mid j \in \mathbb{Z} \text { and }\left(k=0,1,2, \ldots, 2^{j}-1\right)\right\}\).
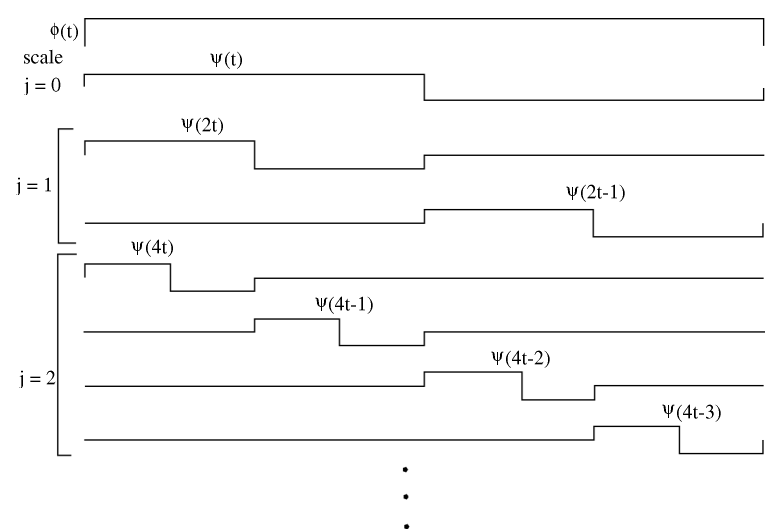
Figure \(\PageIndex{5}\)
\[\psi(t)=\left\{\begin{array}{l}
1 \text { if } 0 \leq t<\frac{T}{2} \\
-1 \text { if } 0 \leq \frac{T}{2}<T
\end{array}\right. \nonumber \]
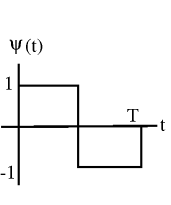
Figure \(\PageIndex{6}\)
Let \(\psi_{j, k}(t)=2^{\frac{j}{2}} \psi\left(2^{j} t-k\right)\).
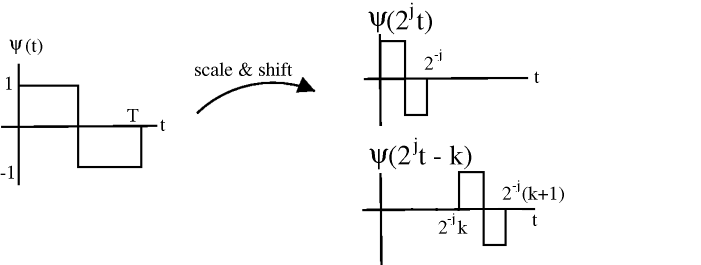
Figure \(\PageIndex{7}\)
Larger \(j\) → "skinnier" basis function, \(j=\{0,1,2, \ldots\}\), \(2^j\) shifts at each scale: \(k=0,1, \ldots, 2^{j}-1\)
Check: each \(\psi_{j, k}(t)\) has unit energy
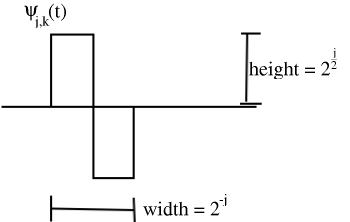
Figure \(\PageIndex{8}\)
\[\left(\int \psi_{j, k}^{2}(t) \mathrm{d} t=1\right) \Rightarrow\left(\left\|\psi_{j, k}(t)\right\|_{2}=1\right) \nonumber \]
Any two basis functions are orthogonal.
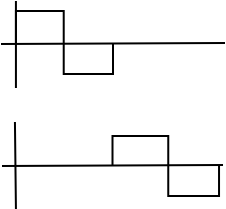
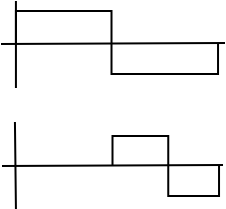
(b) Different Scale
Also, \(\left\{\psi_{j, k}, \phi\right\}\) span \(L^2([0,T])\).
Haar Wavelet Transform
Using what we know about Hilbert spaces (Section 15.4): For any \(f(t) \in L^{2}([0, T])\), we can write
Synthesis
\[f(t)=\sum_{j} \sum_{k} w_{j, k} \psi_{j, k}(t)+c_{0} \phi(t) \nonumber \]
Analysis
\[w_{j, k}=\int_{0}^{T} f(t) \psi_{j, k}(t) d t \nonumber \]
\[c_{0}=\int_{0}^{T} f(t) \phi(t) d t \nonumber \]
Note
the \(w_{j,k}\) are real
The Haar transform is super useful especially in image compression
Haar Wavelet Demonstration
