17.2: Getting Started with Mathematica
- Page ID
- 22950
What is Mathematica?
Mathematica is a computational software program used in technical fields. It is developed by Wolfram Research. Mathematica makes it easy to visualize data and create GUIs in only a few lines of code.
How can I run, create, and find Mathematica files?
Run
The free CDF Player is available for running non-commercial Mathematica programs. The option exists of downloading source files and running on your computer, but the CDF-player comes with a plug-in for viewing dynamic content online on your web browser!
Create
Mathematica 8 is available for purchase from Wolfram. Many universities (including Rice) and companies already have a Mathematica license. Wolfram has a free, save-disabled 15-day trial version of Mathematica.
Find
Wolfram has thousands of Mathematica programs (including source code) available at the Wolfram Demonstrations Project. Anyone can create and submit a Demonstration. Also, many other websites (including Connexions) have a lot of Mathematica content.
What do I need to run interactive content?
Mathematica 8 is supported on Linux, Microsoft Windows, Mac OS X, and Solaris. Mathematica's free CDF-player is available for Windows and Mac OS X, and is in development for Linux; the CDF-Player plugin is available for IE, Firefox, Chrome, Safari, and Opera.
How can I upload a Mathematica file to a Connexions module?
Go to the Files tab at the top of the module and upload your .cdf file, along with an (optional) screenshot of the file in use. In order to generate a clean bracket-less screenshot, you should do the following:
- Open your .cdf in Mathematica and left click on the bracket surrounding the manipulate command.
- Click on Cell->Convert To->Bitmap.
- Then click on File->Save Selection As, and save the image file in your desired image format.
Embed the files into the module in any way you like. Some tags you may find helpful include image, figure, download, and link (if linking to an .cdf file on another website). The best method is to create an interactive figure, and include a fallback png image of the cdf file should the CDF image not render properly. See the interactive demo/image below.
Convolution Demo
<figure > <media alt="timeshiftDemo"> <image mime-type="image/png" src="Convolutiondisplay-4.cdf" thumbnail="Convolution4.0Display.png" width="600"/> <object width="500" height="500" src="Convolutiondisplay-4.cdf" mime-type="application/vnd.wolfram.cdf" for="webview2.0"/> <image mime-type="application/postscript" for="pdf" src="Convolution4.0Display.png" width="400"/> </media> <caption>Interact (when online) with a Mathematica CDF demonstrating Convolution. To Download, right-click and save target as .cdf.%lt;/caption> </figure>
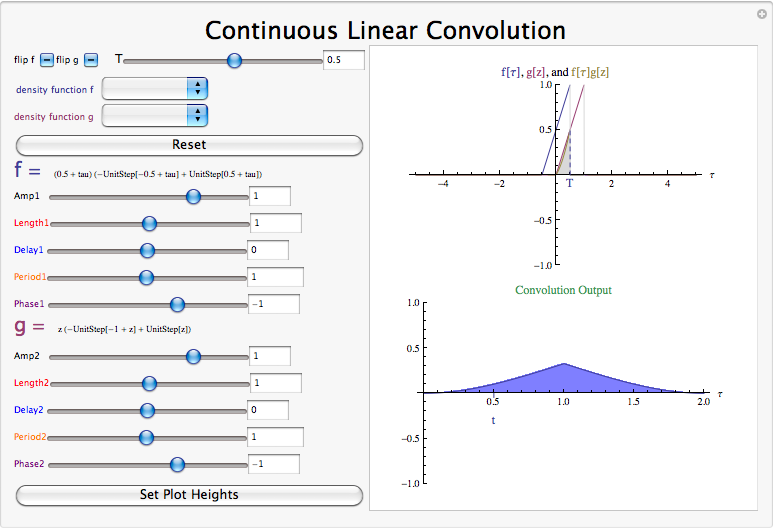
Alternatively, this is how it looks when you use a thumbnail link to a live online demo.

How can I learn Mathematica?
Open Mathematica and go to the Getting Started section of the "Welcome to Mathematica" screen, or check out Help: Documentation Center.
The Mathematica Learning Center has lots of screencasts, how-tos, and tutorials.
When troubleshooting, the error messages are often unhelpful, so it's best to evaluate often so the problem can be easily located. Search engines like Google are useful when you're looking for an explanation of specific error messages.


