2.2: Coin-flip Game

The abstractions of atoms, bonds, and bond energies have been made for us by the development of science. But we often have to make new abstractions. To develop this skill, we’ll analyze a coin game where two players take turns flipping a (fair) coin; whoever first tosses heads wins.

What is the probability that the first player wins?

First get a feel for the game by playing it. Here is one round: TH. The first player missed the chance to win by tossing tails (T); but the second player tossed heads (H) and won.

Playing many games might reveal a pattern to us or suggest how to compute the probability. However, playing many games by flipping a real coin becomes tedious. Instead, a computer can simulate the games, substituting pseudorandom numbers for a real coin. Here are several runs produced by a computer program. Each line begins with 1 or 2 to indicate which player won the game; the rest of the line shows the coin tosses. In these ten iterations, each player won five times. A reasonable conjecture is that each player has an equal chance to win. However, this conjecture, based on only ten games, cannot be believed to strongly.

2TH
2TH

1H

2TH

1TTH

2TTTH

2TH

1H

1H

1H

Let’s try 100 games. Now even counting the wins becomes tedious. My computer counted for me: 68 wins for player 1, and 32 wins for player 2. The probability of player 1’s winning now seems closer to 2/3 than to 1/2.

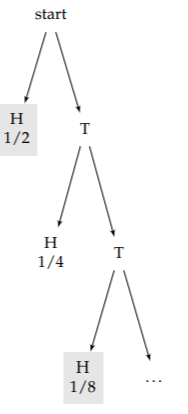
To find the exact value, let’s diagram the game as a tree reflecting the alternative endings of the game. Each layer represents one flip. The game ends at a leaf, when one player has tossed heads. The shaded leaves show the first player’s wins—for example, after H, TTH, or TTTTH. The probabilities of these winning ways are 1/2 (for H), 1/8 (for TTH), and 1/32 (for TTTTH). The sum of all these winning probabilities is the probability of the first player’s winning:

\(\frac{1}{2} + \frac{1}{8} + \frac{1}{32} + ...\)

To sum this infinite series without resorting to formulas, make an abstraction: Notice that the tree contains, one level down, a near copy of itself. (In this problem, the abstraction gets reused within the same problem. In computer science, such a structure is called recursive.) For if the first player tosses tails, the second player starts the game in the position of the first player, with the same probability of winning.

To benefit from this equivalence, let’s name the reusable idea, namely the probability of the first player’s winning, and call it p. The second player wins the game with probability p/2: The factor of 1/2 is the probability that the first player tosses tails; the factor of p is the probability that the second player wins, given that the first player blew his chance by tossing tails on the first toss.

Because either the first or the second player wins, the two winning probabilities add to 1:

\[\underbrace{p}_{P(\textrm{first player wins})} + \underbrace{p/2}_{P(\textrm{second player wins})} = 1.\]

The solution is p = 2/3, as suggested by the 100-game simulation. The benefit of the abstraction solution, compared to calculating the infinite probability sum explicitly, is insight. In the abstraction solution, the answer has to be what it is. It leaves almost nothing to remember. An amusing illustration of the same benefit comes from the problem of the fly that zooms back and forth between two approaching trains.

If the fly starts when the trains are 60 miles apart, each train travels at 20 miles per hour, and the fly travels at 30 miles per hour, how far does the fly travel, in total, before meeting its maker when the trains collide? (Apologies that physics problems are often so violent.)

Right after hearing the problem, John von Neumann, inventor of game theory and the modern computer, gave the correct distance. “That was quick,” said a colleague. “Everyone else tries to sum the infinite series.” “What’s wrong with that?” said von Neumann. “That’s how I did it.” In Problem 2.7, you get to work out the infinite-series and the insightful solutions.

Exercise \(\PageIndex{1}\): Summing a geometric series using abstraction

Use abstraction to find the sum of the infinite geometric series

\[1 + r + r^{2} + r^{3} + ...\]

Exercise \(\PageIndex{2}\): Using the geometric-series sum

Use Problem \(\PageIndex{1}\): to check that the probability of the first player’s winning is 2/3:

\(p = \frac{1}{2} + \frac{1}{8} + \frac{1}{32} + ... = \frac{2}{3}\)

Exercise \(\PageIndex{3}\): Nested square roots

Evaluate these infinite mixes of arithmetic and square roots:

\(\sqrt{3 \times \sqrt{3 \times \sqrt{3 \times \sqrt{3 \times ...}}}}\)

\(\sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + ...}}}}\)

Exercise \(\PageIndex{4}\): Two trains and a fly

Find the insightful and the infinite-series solution to the problem of the fly and the approaching trains (Section 2.2). Check that they give the same answer for the distance that the fly travels!

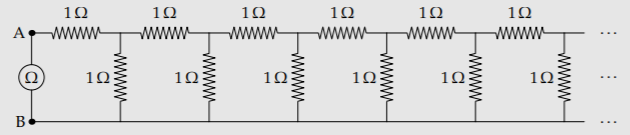
Exercise \(\PageIndex{5}\): Resistive ladder

In the following infinite ladder of 1-ohm resistors, what is the resistance between points A and B? This measurement is indicated by the ohmmeter connected between these points.