Ladder Operators

Mathematically, a ladder operator is defined as an operator which, when applied to a state, creates a new state with a raised or lowered eigenvalue\(^{[1]}\). Their utility in quantum mechanics follows from their ability to describe the energy spectrum and associated wavefunctions in a more manageable way, without solving differential equations. We will discuss the most prominent example of the use of these operators; the quantum harmonic oscillator. Their use does not end there, however, as the mathematics of ladder operators can easily be extended to more complicated problems, including angular momentum and many body problems. In the latter case, the operators serve as creation and annihilation operators; adding or subtracting to the number of particles in a given state.

Quantum Harmonic Oscillator

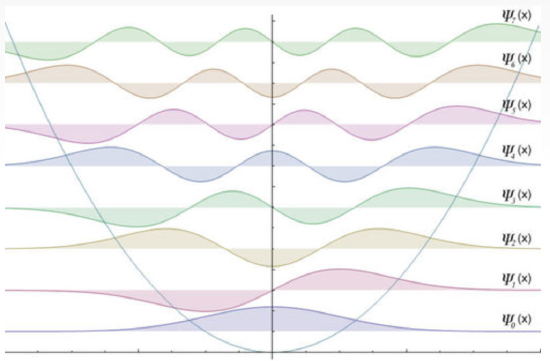
This diagram shows the energy levels and wavefuntions for the harmonic oscillator potential. Image taken from ref \(^{[2]}\)

The one dimensional harmonic oscillator is often referred to in quantum mechanical calculations as many systems can be approximated by that potential when close to an equilibrium point \(^{[4]}\). As we know, for the harmonic oscillator, the potential is given by

\(V(x)={\frac{1}{2}}m{\omega}^2x^2\)

In class, we discussed the energy spectrum and solutions for the time-independent Schrödinger equation, which in this case is the following:

\[-\frac{{\hbar}^2}{2m}\frac{d^2\psi}{dx^2}+\frac{1}{2}m{\omega}^2x^2\psi=E\psi\nonumber\]

In this formulation, our operators are defined using the coordinate basis. Notice the first term represents kinetic energy \(\frac{P^2}{2m}\), while the second represents the potential. Accordingly, we have operators for momentum and position as follow:

\(\boldsymbol{P}=-i\hbar\frac{d}{dx}\) \(\boldsymbol{X}=x \)

Of course, other bases exist, including the momentum basis or the energy basis, in which the expression of these operators might be different. The true beauty of the ladder operator method is that we can define the Hamiltonian in the energy basis without specifying the form of the operators. All that is needed is knowledge of their commutator, which is independent of basis. We will return to this idea later. For the moment, we can continue by rewriting the above Schrödinger equation to show explicitly the operation on \(\psi\).

\[\frac{1}{2m}[{(\frac{\hbar}{i}\frac{d}{dx}})^2+({m\omega x})^2]\psi=E\psi\nonumber\]

Factorization

The ladder operator method is sometimes referred to as the “method of factorization” because the next step involves defining the factor of the term in brackets \(^{[3]}\). If we were dealing with numbers rather than operators, it would be clear that

\[c^2+d^2=(c-id)(c+id)\nonumber\]

In the case of operators, we cannot assume that \(cd=dc\). However, we can continue the examination by defining two new operators, corresponding to the two sets of parenthesis above.

\[a=\frac{1}{\sqrt{2m}}{(\frac{\hbar}{i}\frac{d}{dx}}-im\omega x)i\nonumber\]

\[a^{\dagger}=\frac{1}{\sqrt{2m}}{(\frac{\hbar}{i}\frac{d}{dx}}+im\omega x)i\nonumber\]

Or, in terms of the previously defined position and momentum operators,

\[a=\frac{1}{\sqrt{2m}}(\boldsymbol{P}-im\omega \boldsymbol{X})\nonumber\]

\[a^{\dagger}=\frac{1}{\sqrt{2m}}(\boldsymbol{P}+im\omega \boldsymbol{X})\nonumber\]

These are our ladder operators. To facilitate their use, we need to determine their commutation relation. We can easily show \([\boldsymbol{X},\boldsymbol{P}]=i\hbar\). Using the definition of the commutator \([\boldsymbol{X},\boldsymbol{P}]=\boldsymbol{XP}-\boldsymbol{PX}\)

\[[\boldsymbol{X},\boldsymbol{P}]f(x)=(\boldsymbol{XP}-\boldsymbol{PX})f(x)=x\frac{\hbar}{i}\frac{d}{dx}f(x)-\frac{\hbar}{i}\frac{d}{dx}xf(x)\nonumber\] \[=x\frac{\hbar}{i}\frac{d}{dx}f(x)-f(x)\frac{\hbar}{i}\frac{d}{dx}x-x\frac{\hbar}{i}\frac{d}{dx}f(x)\nonumber\] \[=-f(x)\frac{\hbar}{i}=i\hbar f(x)\nonumber\] Dropping our test function f(x), we see the commutator is indeed \(i\hbar\). Now we compute the products of our ladder operators. \[a a^{\dagger}=\frac{1}{2m}(\boldsymbol{P}-im\omega \boldsymbol{X})(\boldsymbol{P}+im\omega \boldsymbol{X})\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+{im\omega \boldsymbol{PX}}-im\omega \boldsymbol{XP}+({m\omega \boldsymbol{X}})^2)\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2-im\omega (\boldsymbol{XP}-\boldsymbol{PX}))\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2-im\omega [\boldsymbol{X},\boldsymbol{P}])\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2+m\omega \hbar)\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2-im\omega i\hbar)\nonumber\] \[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2)+\frac{1}{2}\hbar \omega\nonumber\] Similarly,

\[a a^{\dagger}=\frac{1}{2m}(\boldsymbol{P}+im\omega \boldsymbol{X})(\boldsymbol{P}-im\omega \boldsymbol{X})\nonumber\]

\[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2+im\omega [\boldsymbol{X},\boldsymbol{P}])\nonumber\]

\[=\frac{1}{2m}({\boldsymbol{P}}^2+({m\omega \boldsymbol{X}})^2)-\frac{1}{2}\hbar \omega\nonumber\]

Notice that the first term is simply the sum of the energies, \(\boldsymbol{H}\).

\[a^{\dagger} a=\boldsymbol{H}-\frac{1}{2}\hbar \omega\nonumber\]

\[\boldsymbol{H}=a a^{\dagger}+\frac{1}{2}\hbar \omega\nonumber\]

Also, from above

\[a a^{\dagger}=\boldsymbol{H}+\frac{1}{2}\hbar \omega\nonumber\]

\[\boldsymbol{H}=a a^{\dagger}-\frac{1}{2}\hbar \omega\nonumber\]

And therefore

\[[a, a^{\dagger}]=a a^{\dagger}-a^{\dagger} a=\hbar \omega\nonumber\]

Often times, the ladder operators are each defined with a multiple of \(\sqrt{\hbar \omega}\) so as to make this commutator equal to one and describe the energies in units of \(\hbar \omega\) \(^{[3]}\). We will continue with the present definition for the moment.

Schrödinger Equation in terms of ladder operators

Note the Schrödinger equation becomes

\[(a a^{\dagger}+\frac{1}{2}\hbar \omega)\psi=E\psi\nonumber\]

Here is where the ladder operators become especially useful. If \(\psi\) is a solution of the equation, we can demonstrate that \(a^{\dagger}\psi\) is also. Keeping the commutator in mind,

\[(a^{\dagger} a+\frac{1}{2}\hbar \omega)(a^{\dagger}\psi)=(a^{\dagger}aa^{\dagger}+\frac{1}{2}\hbar \omega a^{\dagger})\psi\nonumber\]

\[a^{\dagger}(aa^{\dagger}+\frac{1}{2}\hbar \omega)\psi=a^{\dagger}((\hbar \omega a^{\dagger}a)+\frac{1}{2}\hbar \omega)\psi\nonumber\]

\[a^{\dagger}(\hbar \omega\psi+(a^{\dagger}a+\frac{1}{2}\hbar \omega)\psi)=(E+\hbar \omega)(a^{\dagger}\psi)\nonumber\]

In the same manner,

\[(a^{\dagger} a+\frac{1}{2}\hbar \omega)(a\psi)=(a^{\dagger}aa+\frac{1}{2}\hbar \omega a)\psi\nonumber\]

\[((aa^{\dagger}-\hbar \omega)a)\psi=a(-\hbar \omega \psi+(aa^{\dagger}+\frac{1}{2}\hbar \omega)\psi)\nonumber\]

\[a(-\hbar \omega\psi+E\psi)=(E-\hbar \omega)(a\psi)\nonumber\]

So, \(a^{\dagger}\psi\)is an eigenvector with an energy one unit \(\hbar \omega\) greater than \(\psi\), and \(a\psi\) is a solution of the hamiltonian with one \(\hbar \omega\) less energy than \(\psi\). The operators can be said to have created or annihilated one quanta of energy equal to \(\hbar \omega\). For this reason they are also termed creation \(a^{\dagger}\) and annihilation \(a\) operators \(^{[5]}\). Furthermore, starting with any solution, we can simply apply the ladder operators successively to generate any other solution.

We know the harmonic oscillator contains a ground state with minimum energy, below which no state exists. Then, if we apply the annihilation operator, we must get 0 as the result. In other words, a “lowest rung” must exist on our ladder of allowed energies and states \(^{[4]}\).

\[a\psi_{0}=0\nonumber\]

Or, inserting our first definition for the lowering operator, we can solve for \(\psi_{0}\)

\[\frac{1}{\sqrt{2m}}(\frac{\hbar}{i}\frac{d}{dx}\psi_{0}-im\omega x\psi_{0})=0\nonumber\]

\[\frac{d}{dx}\psi_{0}=-\frac{m\omega x}{\hbar}\psi_{0}\nonumber\]

This can be solved with simple integration

\[\int\frac{1}{\psi_{0}}d\psi_{0}=-\frac{m\omega}{\hbar}\int xdx\nonumber\]

\[\ln{\psi_{0}}=-\frac{m\omega}{\hbar}(\frac{1}{2}x^2+C)\nonumber\]

\[\psi_{0}(x)=A_{0}e^{-\frac{m\omega}{2\hbar}x^2}\nonumber\]

Where \(A_{0}\) is a normalization constant, in this case \((\frac{m\omega}{\pi\hbar})^{\frac{1}{4}}\). So, assuming a lowest state allowed us to infer its form, if we chose a basis to express the operator in. Even without specifying a formulation, we can find the energy of that level \(^{[3]}\), which clearly should not depend on basis.

\[a\psi_{0}=0\nonumber\]

\[a^{\dagger}a\psi_{0}=0\nonumber\]

\[(\boldsymbol{H}-\frac{1}{2}\hbar\omega)\psi_{0}=0\nonumber\]

\[\boldsymbol{H}\psi_{0}=\frac{1}{2}\hbar\omega\psi_{0}\nonumber\]

\[E_{0}\psi_{0}=\frac{1}{2}\hbar\omega\psi_{0}\nonumber\]

\[E_{0}=\frac{1}{2}\hbar\omega\nonumber\]

We can define the number operator as

\[\boldsymbol{N}=\frac{a^{\dagger}a}{\hbar\omega}\nonumber\]

Where, again, many formulations of ladder operators incorporate the divisor into the operators themselves. The number operator, when acting on a state, simply returns the number of the current energy level. Using ladder operators, then, we have completely defined the harmonic oscillator states and energy levels

\(\psi_{n}(x)=A_{n}(a^{\dagger})^ne^{-\frac{m\omega}{2\hbar}x^2}\) \(E_{n}=(n+\frac{1}{2})\hbar\omega\)

Conclusion

Ladder operators are seen in many facets of quantum mechanics. Earlier, we defined the ladder operators in terms of momentum and position operators. With little effort, we could easily define \(\boldsymbol{X}\) and \(\boldsymbol{P}\) as linear combinations of the ladder operators. Because many of the potentials we are concerned with are functions of position only, ladder operators for other systems can be defined in a similar way. These formulations offer a method of working with such problems without solving the differential equations.

In the theory of quantum fields, the momentum and potential of a region are simultaneously described in space-time by a state field. The mechanism of creation and annihilation operators is essential in this case, allowing us to describe the state as a combination of these operators, thus quantizing the field \(^{[6]}\).

We have seen that ladder operators and their commutator relationship are all that are needed to completely solve the quantum harmonic oscillator. We were able to do so without ever actually addressing the choice of basis or solving the differential equations (though I did both in order to write a recognizable form of the ground state, we could leave our work in terms of the operators). Were this the only case where ladder operators proved useful, they would still merit much study. Fortunately, they find wide use in other application of quantum theory, and often make calculations much easier.

Bibliography

1. en.Wikipedia.org/wiki/Ladder_operators
2. en.Wikipedia.org/wiki/Quantum...nic_oscillator
3. Shankar, R. Principles of Quantum Mechanics2nd ed. (chp. 7), New Haven:Plenum Press, 1994
4. Griffiths, D. Introduction to Quantum Mechanics(chp. 2), NJ: Prentice Hall, 1995
5. en.Wikipedia.org/wiki/Creatio...tion_operators
6. Schiff, L. Quantum Mechanics3rd ed. (chp. 14)/ New York: McGraw-Hill, 1968

Contributors and Attributions

• ContribMSE5317