Lattice Vibrations

Almost all solids with the exception of amorphous solids and glasses have periodic arrays of atoms which form a crystal lattice \(^{[1]}\). The existence of the periodic crystal lattice in solid materials provides a medium for characteristic vibrations. Between the lattice spacing, there are quantized vibrational modes called a phonon. \(^{[2]}\) The study of phonon is an important part of solid state physics, as they play an essential role in the physical properties of solids, the thermal and electrical conductivity of the materials. The long wavelength property of phonon also gives attributes to sounds in solids. Phonons are also a quantum mechanical version of a special type of vibrational motion. This type of vibrational motion is called a normal mode (elementary blocks of lattice vibration), which is a pattern of motion in which all parts of the system move in a sinusoidal fashion, with the same frequency\(^{[3]}\). An example of a normal mode is a standing wave, which is a continuous form of normal mode and all space elements, (x, y and Z co-ordinates) are oscillating at the same frequencies, and phase but different amplitude.

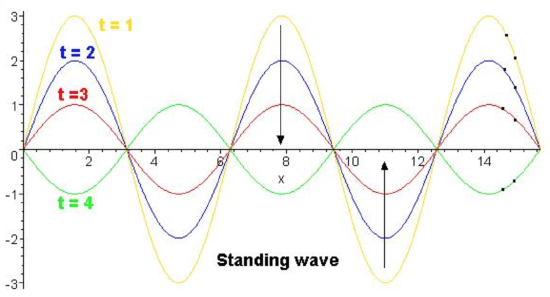
Figure \(\PageIndex{1}\) Standing Wave Standing wave in stationary medium. The red dots represent the wave nodes.

The general form of a standing wave is:

\[ f(x, y, z) \label{1} \]

where \(f(x, y, z)\) represents the dependence of amplitude on location and the cosine and sine are the oscillations in time. A₀ represents the amplitude of the cosine waves.

Lattice Vibrations

Lattice vibrations can explain sound velocity, thermal properties, elastic properties and optical properties of materials. Lattice Vibration is the oscillations of atoms in a solid about the equilibrium position. For a crystal, the equilibrium positions form a regular lattice, due to the fact that the atoms are bound to neighboring atoms. The vibration of these neighboring atoms is not independent of each other. A regular lattice with harmonic forces between atoms and normal modes of vibrations are called lattice waves. Lattice waves range from low frequencies to high frequencies on the order of 1,013 Hz or even higher \(^{[4]}\). However, the wavelengths at extremely high frequencies are of the order of inter atomic spacing. Due to the shortness of these wavelengths, the motion of the neighboring atoms is uncorrelated; with each atom moving about its average position in three dimensions with average vibrational energy, which is usually 3kT, with ‘\(k\)’ representing the Boltzmann constant and '\(T\)' the absolute temperature. Lattice vibrations can also interact with free electrons in a conducting solid which gives rise to electrical resistance \(^{[4]}\).

Optical Properties of Lattice Vibrations

Compared to the static lattice model that deals with the average positions of atoms in a crystal; lattice dynamics works towards extending the concept of crystal lattice to an array of atoms with finite masses capable of motion. The motion of masses is a superposition of vibrations of atoms around the equilibrium sites induced by the interaction with neighboring atoms. The collective vibration of the atoms within the crystal forms a wave of allowed wavelength and amplitude. For example, as we know that light is said to be a wave motion composed of photons, we can also think of the normal modes of vibration in a solid as being a particle. One major problem with Lattice dynamics is that is hard to find the normal modes of vibration of the crystal. However, lattice dynamic, offers two different ways of finding the dispersion relation within the lattice\(^{[6]}\).

1. Quantum-mechanical approach: Quantum-mechanical approach can be used to obtain phonon's dispersion relation. In order to do so, the solution to the Schrödinger equation for the lattice vibrations must be solved. The quantum-mechanical operators for the normal mode coordinates are substituted in the phonon Hamiltonian by the creation and annihilation operators.
2. Semi-classical treatment of lattice vibrations: The semi-classical treatment gives classical mechanics the use of one additional postulate taken from quantum mechanics, mainly that the energy of lattice vibrations is quantized. The classical motions of any atom are determined by Newton's law of mechanics: force=mass x acceleration. Formally, if \(r(t)\) is the position of atom at time \(t\), then \[ \dfrac{\partial ^2 r(t)}{\partial t^2} = -\dfrac{1}{m} \nabla \phi (r,t) \label{2}\] where \(m\) is the atomic mass, and \(\phi (r,t)\) is the instantaneous potential energy of the atom with the other atoms within the crystal.

Optical Phonons

Optical phonon are quantized modes of lattice vibrations when two or more charged particles in a primitive cell move in opposite directions with the center of mass at rest. This mode has highest energy for wavelength infinity or \(k=0\) when the two lattices move in opposing direction of each other.

Let’s consider a lattice with two kinds of atoms with masses \(m\) and \(M\). The equations of motion are:

\[m\dfrac{\partial ^2 U_{2n}}{\partial ^2 t}=\beta(U_{2n+1}-2U_{2n}+U_{2n-1})\label{3a}\]

\[m\dfrac{\partial ^2 U_{2n+1}}{\partial ^2 t}=\beta(U_{2n+2}-2U_{2n+1}+U_{2n})\label{3b}\]

for atom with masses '\(m\)' and ‘\(M\)’ respectively

\[U_{2n}=Ae^{i(2nka\pm \omega t)}\label{4a}\]

\[U_{2n+1}=Ae^{i((2n+1)ka\pm \omega t)}\label{4b}\]

The solution of the diatomic lattice is

\[{\omega}^2=\beta \left(\frac{1}{m}+\frac{1}{M}\right) \pm \beta\sqrt{\left(\dfrac{1}{m}+\dfrac{1}{M}\right)^2-\frac{4{\sin}^2 ka}{Mm}}\label{5}\]

The plot of the solution is

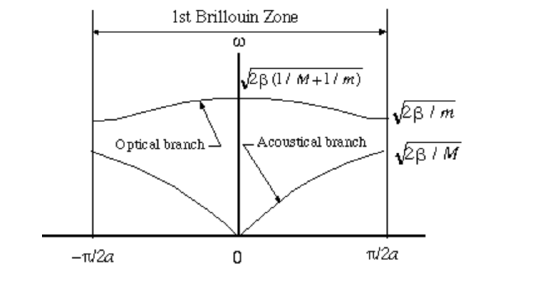
Figure \(\PageIndex{2}\) More information on Brillouin Zones.

The frequencies that are allowed to propagate, their waves are split into an upper and lower branch called the optical and acoustical branch respectively. The gap (forbidden band) between the optical and acoustic branch is the region where frequencies are not allowed to propagate. The width of this forbidden band depends on the difference of the masses of the two atoms. If the two masses are equal, the two branches join (become degenerate) at \(\pi/2a\). The acoustical branch for the diatomic is similar to that of the monatomic lattice, but the optical branch is different \(^{[7]}\). The difference between the optical and acoustic branch is that the optical branch for the long wavelength limit both atoms in the unit cell move opposite to each other with an increase in the mass amplitude. The acoustical branch for the long wavelength limit, the displacement of both atoms has the same amplitude, direction and phase\(^{[7]}\).

Acoustic Phonons

Acoustical phonons are phonons whose frequency which goes to zero in the limit of small \(k\). Let’s consider monatomic a linear chain of identical atoms of mass ‘M’ spaced at a distance ‘\(a\)’, the lattice constant, connected by invisible Hook's law springs and longitudinal deformations\(^{[8]}\).

• \(U_n\) =displacement of atom n from its equilibrium position
• \(U_{n-1}\)=displacement of atom n-1 from its equilibrium position
• \(U_{n+1}\)=displacement of atom n+1 from its equilibrium position

The force on atom ‘n’ will be given by its displacement and the displacement of its nearest neighbors:

\[ F_n = \beta (U_{n+1} - 2U_n + U_{n-1}) \label{6}\]

The equation of motion is:

\[M \dfrac{\partial^2 U_n}{\partial t^2} = \beta (U_{n+1} - 2U_n + U_{n-1}) \label{7}\]

where \(\beta\) is a spring constant.

With wave solution

\[U_n = U_{no} e^{[i(kna \pm \omega t)]} \label{8}\]

If \(U_{no} = U_o\) and has a definite amplitude.

Substitute Equations \ref{5} into Equations \ref{4a} and \ref{4b} we obtain phonon's dispersion relation for linear monatomic chain as follows:

\[ \omega = \pm \sqrt{\dfrac{4\beta}{M}} \sin \left( \dfrac{ka}{2} \right) \label{9}\]

with dispersion curve

Figure \(\PageIndex{3}\)

1.6 Phonons in 3-Dimension

In a 3-D crystal, the atoms vibrate in three dimensions with three vibrational branches, one longitudinal and two transverse. For a 3-D Lattice with N atom per lattice point, there is 3(m-1) optical branches, of which 2(m-1) are transverse optical phonons and the remaining phonons are longitudinal optical phonons. In a transverse wave, the atomic displacement direction is perpendicular to the direction of the propagated wave. The remaining two transverse waves will overlap if the two vibrational directions are symmetric. In regards to electrons, the phonons are dispersed along different crystallographic direction\(^{[5]}\).

Figure \(\PageIndex{4}\): Collective motions called phonons (Public Domain; Sean Kelley via NIST)

References

1. http://hyperphysics.phy-astr.gsu.edu...s/lattice.html
2. en.Wikipedia.org/wiki/Phonon
3. crd.lbl.gov/~chao/nma.html
4. http://www.answers.com/topic/lattice-vibration
5. Nanoscale EnergyTransport and Conversion By Lang Cher pg 105
6. The Crystal Lattice By Arnolʹd Markovich Kosevich
7. Optical Phonon-http://www.chembio.uoguelph.ca/educmat/chm729/Phonons/optical.htm
8. Acoustical Phonon-http://www.chembio.uoguelph.ca/educmat/chm729/Phonons/monatom.htm

Contributors and Attributions

• ContribMSE5317