Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

Hall Effect

Last updated

Sep 8, 2021
Save as PDF
- Ferroelectricity
- Ladder Operators

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Hall Effect, deflection of conduction carriers by an external magnetic field, was discovered in 1879 by Edwin Hall. It has been known that moving carriers in a magnetic field are accelerated by the Lorentz Force, and the magnitude and the direction of the applied force on the carriers are given as in Equation (1):

$\mathbf{F} = q\boldsymbol{v}\times \mathbf{B} \label{1}$

Where $q$ is electron charge, $\mathbf{v}$ is drift velocity and $\mathbf{B}$ is magnetic flux density. If $\mathbf{B}$ is perpendicular to current flow direction as seen in Figure $\PageIndex{1}$ , then the direction of the force is found by right hand rule and magnitude is expressed as scalar multiplication of $q$ , $v$ and $B$ .

Figure $\PageIndex{1}$ : Hall Effect measurement setup for electrons. Initially, the electrons follow the curved arrow, due to the magnetic force. At some distance from the current-introducing contacts, electrons pile up on the left side and deplete from the right side, which creates an electric field $\xi_y$ in the direction of the assigned VH. VH is negative for some semi-conductors where "holes" appear to flow. In steady-state, $\xi_y$ will be strong enough to exactly cancel out the magnetic force, so that the electrons follow the straight arrow (dashed). (public domain; Gnefgnoix). $^{[2]}$

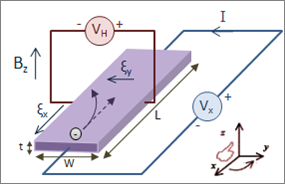
Figure $\PageIndex{1}$ shows a conductive slab with a current $I_x$ in x-direction, and with width $w$ and thickness $t$ . An external magnetic flux density ( $B_z$ ) is applied in z direction, resulting a Lorentz force in –y direction for holes and electrons (due to negative charge of electrons). Material shown in Figure $\PageIndex{1}$ is a p-type semiconductor (doped with acceptor atoms). Without application of any magnetic field, holes flow through by experiencing no force along the y-direction. However, once $B$ is applied, holes are deflected in –y direction resulting a (+) charge accumulation on the side A. Since the material has to be neutral, same amount of charge with opposite sign (-) appears on the other side of the slab (side $B$ ). Source of this negative charge on side B is negatively charged dopant ions. An internal electrical field ( $\varepsilon_y$ ) starts building. As more charge accumulates on the sides, (\varepsilon_y\) gets stronger and opposes the Lorentz force. Eventually, electrical force ( $F_y=q\varepsilon_y$ ) cancels out the Lorentz force ( $-qvB_z$ ) and results:

$\varepsilon_{y} = v B_{z} \label{2}$

Also, current density ( $J_x$ ) and the drift velocity ( $v$ ) are also related with:

$J_{x} = pqv \label{3}$

Where p is the hole density of the material. When $v$ in (3) is substituted in (2):

$\varepsilon _{y} = \dfrac{J_{x}B_{z}}{pq} \label{4}$

is achieved. Also, voltage potential difference between $A$ and $B$ ( $V_{AB}$ ) can be written as:

$V_{AB} = \dfrac{R_{H}I_{x}B_{z}}{t} \label{5}$

Where $R_H$ (=1/qp)is Hall coefficient. In (5), all parameters except $R_H$ are known or can be measured, which gives solution to $R_H$ , so p. If a similar derivation is performed for an n-type material (majority carriers are electrons), $R_H= -1/ qn$ will be achieved. Since $R_H$ is found to be positive for p-type material and negative for the n-type, Hall coefficient can be measured to analyze the type of majority carrier of an unknown material.

Furthermore, if the resistivity ( $\rho$ ) of the material is known (or measured) mobility of the carriers can also be extracted as given:

$\mu_{h}=\dfrac{\sigma }{qp}=\dfrac{R_{h}}{\rho } \label{6}$

Where $\mu_p$ is hole mobility. Relation in (6) enables mobility measurements of majority carriers for single carrier materials.

Figure $\PageIndex{2}$ Hall effect in presence of both holes (h) and electrons (e) $^{[3]}$ .

If both holes and electrons are conduction carriers, then a different derivation has to be done to solve for Hall coefficient. Figure $\PageIndex{2}$ shows a semiconductor with holes and electrons flowing through. Magnetic flux density B deflects both carrier types to bottom surface of the material. In this case, Lorentz force on electrons and holes can be written as:

$F_{e}=qv_{e}B \label{7}$

$F_{h}=qv_{h}B \label{8}$

Which result in built in electric fields of:

$\varepsilon_{e}=\dfrac{J_{e}B}{qn} \label{9}$

$\varepsilon_{h}=\dfrac{J_{h}B}{qp} \label{10}$

In transient analysis, current density along y-axis (perpendicular to electrical current flow) can be written using (9) and (10):

$J_{y}=nq\mu_{e}\varepsilon_{e} + pq\mu_{h}\varepsilon_{h}+ (nq\mu_{e} + pq\mu_{h})\varepsilon_{H} \label{11}$

In steady state, current density (net charge flow) along the y-axis has to be zero, which results in Hall coefficient of:

$R_{H}=\dfrac{p\mu_{h}^{2}-n\mu_{e}^{2} }{q(p\mu_{h}+n\mu_{e})^{2}} \label{12}$

Equation (12) indicates that Hall coefficient of a material can either be positive or negative depending on mobility and density of the carriers (electrons and holes). Table $\PageIndex{1}$ shows Hall coefficient of a number of metals. Notice that $R_H$ is positive for some metals, showing holes are the dominant type.

Table $\PageIndex{1}$ *Hall coefficient (Volt m3/Amp Weber) x 10^-10 at room temperature.*
Li	Na	Cu	Ag	Au	Zn	Cd	Al
-1.7	-2.5	-0.55	-0.84	-0.72	+0.3	+0.6	-0.3

References

F. T. Ulaby, Electromagnetics for Engineers. ,4th ed.NJ: Pearson/Prentice Hall, 2005, pp. 397.
B. G. Streetman, Solid State Electronic Devices. ,4th ed.Prentice Hall, 1995.
M. A. Omar, Elementary Solid State Physics: Principles and Applications. MA: Addison Wesley Publishing Company, 1993, pp. 669.

Contributors and Attributions

ContribMSE5317

References

Contributors and Attributions

Support Center

How can we help?