Ferroelectricity
- Page ID
- 321
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
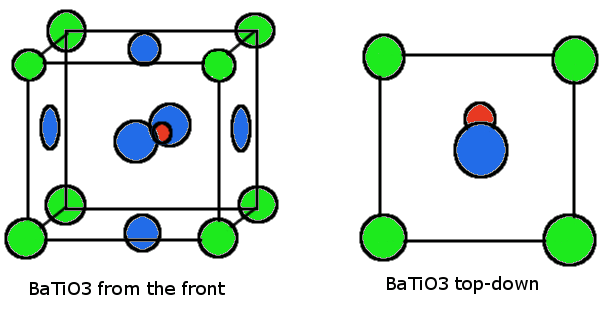
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ferroelectricity is a property observed in certain materials characterized by the presence of a spontaneous electric polarization without the presence of an electric field, much like how ferromagnetism is characterized by a spontaneous, permanent magnetic field. A subclass of piezoelectric and pyroelectric materials, ferroelectric materials are noncentrosymmetric crystals, where some atoms in the unit cell are misplaced to create a permanent electric dipole due to the imbalances observed in the distribution of electric charge. Barium titanate (BaTiO3), a common ferroelectric material with the perovskite crystal structure, portrays this property by displacing the titanium ion at body center 0.05Å along the +b direction and the oxygen atoms 0.08Å in the -b direction, creating a slight dipole moment (figure 1). This displacement, coupled with the relatively small size of the Ti4+ ion, makes it difficult for the titanium ion to bond with all of the oxygen ions.
Crystal Structure and Material Preparation
Ferroelectricity is a displacive phenomenon where ions within the unit cell are placed asymmetrically, creating dipole moments. These asymmetries may form in two different ways, either displacively or by order-disorder. Ferroelectrics with the perovskite crystal structure, like barium titanate (BaTiO3) and lead titanate (PbTiO3), are commonly displacive-type ferroelectrics, where at temperatures below the Curie temperature, ions are displaced slightly from equilibrium to create an asymmetry in the electron population densities, which leads to the permanent dipole moment. In order-disorder ferroelectrics, like NaNO3, the dipoles are present at all temperatures, but are randomly oriented above the Curie temperature. The dipoles align after the temperature is brought below the threshold.
While the individual unit cells of a ferroelectric material possess their own dipole moment, without the presence of an external electric field these moments do not align with each other to produce any long-range symmetry (figure 2a). Within individual grains the polar axes are aligned but across the bulk of the sample there is no net polarization. At sufficiently high temperatures for the grains to break down, and in the presence of an electric field, the polar axes may realign to match the field. If the material is cooled under this field, the polar axes remain aligned, thus forming a substance that has an observable, spontaneous electric dipole (figure 2b). In the case of barium titanate, the titanium ion is displaced in the direction of the electric field and the oxygen ions displaced against it, creating the dipole. With subsequent inputs of alternating electric fields, the dipoles realign by shifting the titanium ion to the other side of the unit cell.
Properties
Ferroelectricity is characterized by the presence of a spontaneous electric dipole while not exposed to an external electric field, much like how ferromagnetism is characterized by a spontaneous magnetic dipole. Above a certain temperature, called the Curie temperature (TCurie), ferroelectric materials lose this polarization and behave like paramagnetic or diamagnetic materials. At the Curie temperature, the energy within the crystal allows the ions to arrange themselves in a stable equilibrium, eliminating the polarization caused by the displacement of one or more ions.

The change in polarity of ferroelectrics with an applied electric field is observed to follow a simple hysteresis loop (figure 3). If the crystal structure of a ferroelectric has been broken down in high heat and not in the presence of an electric field., it is unpolarized as seen in the origin of figure 2. With an applied field, the polarization quickly approaches a point where the polarization is linearly proportional to the applied electric field. If an opposite electric field is applied, the polarity does not change significantly until the field reaches a relatively large magnitude, and the polarity of the ferroelectric reverses and levels off. This loop can be repeated numerous times to alter the polarity of the ferroelectric, often to the order of 1016 cycles depending on the material.
The polarization of ferroelectrics is a non-volatile property once the polarization is set. External electric fields are unable to change the polarization direction unless the magnitude of the field reaches the required threshold, and magnetic fields have negligible effects on the electronic polarization observed.
Applications
Many application of ferroelectric materials utilize the polarization reversal, or switching effect, that the materials experience when exposed to powerful electric fields. This switching effect is utilized in digital memory applications, as reversing the polarity of the material allows for the creation of 0 and 1 bits in computing. As the polarization of ferroelectrics is nonvolatile and does not require extra input to remain polarized, ferroelectrics possess an advantage over traditional semiconductors when it comes to digital storage. Dielectric random access memory (DRAM) in a computer relies on electricity to maintain its storage, and unexpected shutdowns or power outages cause loss of information, allowing the short-term memory modules in computer to behave like back-up long-term memory banks. This property also makes ferroelectrics ideal for electronic access cards, like keycards or transit cards, as their polarized states are not disrupted by magnetic fields and do not decay over time. The ability to maintain its polarization without outside input also means ferroelectric random access memory (FeRAM) only requires energy when it is read or written, while DRAM requires a constant energy input to maintain the information stored. The energy-saving possibilities of FeRAM are therefor highly researched and a leading reason for the development of more efficient FeRAM assemblies.
The hysteretic behavior of the polarization of ferroelectrics also makes them very good candidates for alternatives to dielectrics in capacitors. As the polarization of ferroelectrics can reach very high levels, as well as the possibility of tuning the strength of the dipole according to the strength of the input electric field. As dielectric capacitors cannot be tuned like ferroelectric capacitors, the latter are capable of being made much smaller in comparison to the former.
Questions
- At T>TC, a certain ferroelectric material displays no ferroelectric properties, and through sensitive imaging techniques, it is determined that the material displays a perfect perovskite crystal structure. When T<TC, imaging reveals that the ions within the crystal have shifted slightly and no longer indicate a perfect perovskite crystal, as the ions at body-center have shifted slightly towards individual sides of the unit cells. What kind of ferroelectric phase transformation is observed in this material?
- You have grown a BaTiO3 crystal and apply an electric field to it in order to produce a net dipole. However, when you try to measure the moment there is nothing to be seen. Assuming that your measurement equipment is working properly, what might be the issue with your sample and how might you go about fixing it?
- A brand new ferroelectric has just recently been discovered and you are tasked with determining its viability as a new material to make FeRAM out of. You develop a prototype device and subject it to conditions (rate of electric input, temperature) that RAM modules often experience in computers. The ferroelectric holds up well in tests in the beginning, but loses all ability to store information as tests continue. What might be happening to the ferroelectric in these tests to eliminate the polarizability of the FeRAM module?
Answers
- This is indicative of a displacive phase transformation.
- The grains within the sample may not have their polar axes aligned, so attempts to polarize it are not effective. Increasing the temperature, exposing the substance to an electric field, and then cooling it while in the field will align the polar axes to a certain degree, allowing them to produce a net electric dipole moment.
- Ferroelectrics can be polarized while they are operating at temperatures below their Curie temperature, where the ions within the material have enough energy to combine and form symmetric crystals. As the test continues, the temperature increases past the ferroelectric's Curie temperature and can no longer be polarized.
References
- Damjanovic, D. (2006). Hysteresis in Piezoelectric and Ferroelectric Materials. In The Science of Hysteresis (1st ed., Vol. 3, pp. 337-465). Waltham, Massachusetts: Academic Press.
- Ferroelectric Materials. (n.d.). Retrieved December 9, 2015, from home.sou.edu/~photinos/ferro/nsf_wht.pdf
- Ferroelectric Materials – Properties and Applications of Ferroelectric Materials. (2006, November 21). Retrieved December 9, 2015, from http://www.azom.com/article.aspx?ArticleID=3593
- Fridkin, V., & Ducharme, S. (2014). Ferroelectricity and Ferroelectric Phase Transition. Retrieved December 9, 2015, from www.springer.com/cda/content/...427-p175475682
- Yang, S. (2014, October 26). Faster switching helps ferroelectrics become viable replacement for transistors. Retrieved December 9, 2015, from news.berkeley.edu/2014/10/26/...ric-switching/
Contributors and Attributions
- John Kraska (B.S. Materials Science and Engineering | University of California, Davis | June 2016)

