Fermi Energy and Fermi Surface

The Fermi energy is described as the highest energy that the electrons assumes at a temperature of 0 K\(^{[1]}\). To put this into perspective one can imagine a cup of coffee and the cup shape is the electron band; as one fills the cup with the liquid the top surface increases. This can be compared to the Fermi energy because as electrons enter the electron band the Fermi energy increases. (Attention: Semiconductors act differently than the above stated analogy) The concept of the Fermi energy is crucial to understanding electrical and thermal properties of solids. Below are measured Fermi energies of some materials\(^{[1]}\). Typical ranges of Fermi energy are between 2 eV and 12 eV.

Table \(\PageIndex{1}\) Measured Fermi energies of certain materials\(^{[1]}\).

Material		Ag		Al		Au		Ca		Cu		K		Li		Na		Zn
Fermi Energy Ef (eV)		5.5		11.8		5.5		3.0		7.0		1.9		4.7		3.2		11.0

The distribution of energies with a large number of particles and its change with temperature is described by the Fermi distribution (f(E)), this will be discussed later. This function will exist above the Fermi level. The Fermi level also plays a role in the determination of band energy in solids. In semiconductors, the Fermi level is depicted through its band gap which is shown below in Figure \(\PageIndex{1}\).

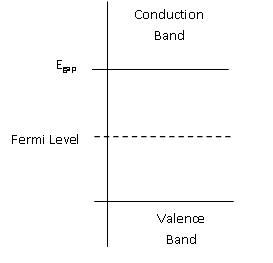
Figure \(\PageIndex{1}\) Depiction of Fermi Level for a semiconductor @ 0K [2]

Another factor that the Fermi energy plays is in the role of understanding specific heat of solids at room temperatures, specifically how the electrons do not contribute it. Because of the small volume of electrons that are in the metals thermal energy kT of the Fermi energy, they are frozen out due to the Pauli principle\(^{[2]}\). This is where an energy level can only accommodate two electrons, one with a spin up and one with a spin down. Below shows a diagram of energy levels that follow the Pauli exclusion principle.

Figure \(\PageIndex{2}\) Occupied energy levels that follow the Pauli exclusion principle

1.2 Fermi Function

Using the Pauli exclusion principle where the interaction between two electrons can not be in the same quantum state (Figure \(\PageIndex{3}\)).

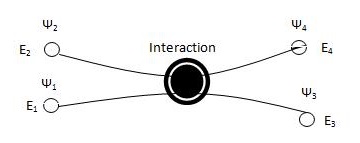
Figure \(\PageIndex{3}\) Two electrons with initial wave functions \(\Psi_1) and \(\Psi_2) at \(E_1\) and \(E_2\) interact and end up at different energies \(E_3\) and \(E_4\) \(^{[3]}\)

We can now assume that each electron will be in its own quantum state \(\Psi\) and will have its own energy associated with it. Using Figure \(\PageIndex{3}\), we need to assume that \(E_3\) and \(E_4\) energies are not occupied. We are going to let f(E) be the probability that the electron is in such a quantum state with is relative energy interaction. This relation deduced from Figure \(\PageIndex{3}\) is

\[f(E1)f(E2)[1-f(E3)][1-f(E4)]\]

where the [ ] brackets represent \(E_3\) and \(E_4\) are empty. Due to the interactions acting in both the reverse and forward directions of the first representation\(^{[1]}\), f(E) must satisfy

\[f(E1)f(E2)[(1-f(E3)][1-f(E4)] = f(E3)f(E4)[1-f(E1)][1-f(E2)] \]

where the solution to Equations (1) and (2) is

\[f(E) = \dfrac{1}{1+ A \exp⁡(E/kT)}\]

where \(A\) is a constant. By substituting Equation (3) into Equation (1) and using Equation (2) one can confirm Equation (3). Let \(A = exp(-E_f/kT)\), one can write Equation (4).

\[f(E) = \left(1+\exp⁡ \left(\dfrac{E-E_f}{kT}\right )\right)^{-1} \]

where \(E_f\) is the Fermi energy\(^{[3]}\).

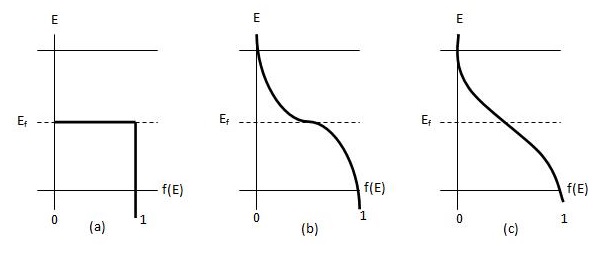
Figure \(\PageIndex{4}\) Fermi distribution function, f(E), versus energy E. (a) T=0, (b) T=\(T_1\), (c) \(T_2\)>\(T_1\)\(^{[4]}\)

The Fermi distribution function for higher temperatures above T=0 is shown in Figure \(\PageIndex{4}\). Note that as temperature increases \(f(E)\) extends to higher energies. At energies above \(E_f\), \(f(E)\) behaves almost like a Boltzmann distribution function:

\[f(E)=\exp \left( \dfrac{-(E-E_f)}{kT} \right)\]

where

\[E-E_f \gg kT\]

When temperatures increase above 0K, at \(E=E_f\), \(f(E) = 1/2\)\(^{[4]}\).

1.2.1 Fermi Distribution Function to Evaluate Specific Heat

To evaluate the specific heat of a material one needs to assume that the electrons around the Fermi level are the only electrons excited. Thus the electrons around kT of the Fermi level are considered and can conclude that only \(kT/E_f\) of the electrons are affected. So per mole the number of electrons excited can be equated as N(kT/Ef). Thermal energy can than be approximated due to the fact that electrons absorb energy, kT, and this is represented by

\[U=\dfrac{N(kT)^2}{E_f} \label{7}\]

and the specific heat is

\[C_v={U'}/{T'}={2R(kT)}/{E_f} \label{8}\]

where U' and T' are partial derivatives and R=Nk.

Substituting \(E_f=KT_f\), where \(T_f\) is the Fermi temperature, one gets

\[ C_v= {2RT}/{T_f} \label{9}\]

An interesting conclusion from Equation (9) is that the heat capacity of electrons is a linear function of temperature. Where the lattice heat capacity is a constant at high temperature and proportional to \(T^3\) at low temperature\(^{[3]}\). Finally an exact equation that exactly represents electronic specific heat is

\[C_v=\left( \dfrac{\pi^2}{2} \right) \dfrac{RT}{T_f} \label{10}\]

Fermi Surface

The Fermi surface is a useful tool to predict many properties of materials. These properties include thermal, electrical, magnetic, and optical properties\(^{[3]}\). The shape is derived from the periodicity and symmetry of the crystalline lattice and energy bands\(^{[1]}\). For the Fermi surface all points in reciprocal space at which \(E=E_f\). In different dimensions there are different representations which include:

• 1D: represented by a pair of points
• 2D: represented by a line (which could be a closed loop)
• 3D: represented by a surface (which could be a closed surface)

Below is a depiction of the Fermi surface and Fermi sphere.

Figure \(\PageIndex{5}\) Fermi surface and Fermi sphere

The ground state of N free electrons is constructed by occupying all one electron levels \(\mathbf{k}\) with energies

\[\epsilon (\(\mathbf{k}\)) = \dfrac{\hbar^2k^2}{2m} < \epsilon_f\]

Where \(\epsilon_f\) is determined by requiring the total number of one electron levels with energies less than \(\epsilon_f\) to be equal to the total number of electrons. When the lowest of these are filled by a specified number of electrons, two quite distinct types of configuration can occur:

• A certain number of bands may be completely filled, all others remaining empty. The band gap is determined by the difference between the highest occupied energy level and the lowest occupied energy level.
• A number of bands may be partially filled. When this occurs, the energy of the highest occupied level, the Fermi energy, lies within the energy range of one or more bands. For each partially filled band there will be a surface in k-space separating the occupied from the unoccupied levels. The set of all such surfaces is known as the Fermi surface. The parts of the Fermi surface arising from the individual partially filled bands are known as branches of the Fermi surface\(^{[5]}\).

Thus the Fermi surface is a constant energy surface in k-space, just as the more familiar equipotentials of electrostatic theory are constant energy surfaces in real space \(^{[4]}\). The Fermi surface is also independent of temperature, when there is an increase in temperature only a small amount of electrons are excited and thus they move from the inside to the outside surface. The value of the Fermi Energy is determined by the electron concentration. So higher the Fermi level the higher the \(E_f\). This is given by

\[E_f=\left( \dfrac{h^2}{2m^*} \right) \left(3\pi^2N \right)^{2/3} \label{11}\]

1.3.1 Fermi Surface and Electrical Conductivity

When an electrical field is applied, the Fermi surface shifts in the direction of the field either in the positive or negative direction. This is shown below in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\) Due to an electric field there is a displacement in the Fermi surface

1.4 Density of Energy States and Fermi level

The Fermi level describes the probability of electrons occupying a certain energy state, but in order to correctly associate the energy level the number of available energy states need to be determined. From there the amount of electrons that could reach the conduction band could be determined.

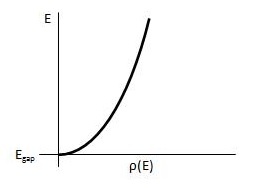
Figure \(\PageIndex{7}\) Density of Energy States in conduction band of a semiconductor [4].

In calculating for the density this equation is used

\[ρ(E)=\dfrac{8\sqrt{2m^{3/2}} }{h^3} \sqrt{ E-E_{gap}} \label{12}\]

Further reading on Density of States can be found by clicking here.

1.5 Band Theory and Fermi Level

The Fermi level plays an important role in the band theory of solids. At low temperatures, the top of the electron energy level is the Fermi level. The position of where the Fermi level is in comparison to the conduction band is a crucial in determining electrical properties of materials. A diagram of different material types are shown below and the relation of the Fermi level to the conduction band.

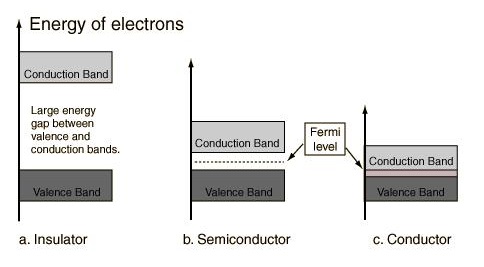
Figure \(\PageIndex{8}\) Energy band in solids \(^{[2]}\)

Further reading on Band Theory can be found by clicking here.

References

1. Electronic Properties of Materials by Hummel
2. http://hyperphysics.phy-astr.gsu.edu...ids/Fermi.html
3. Electronic Materials and Devices by S.O. Kasap
4. Elementary Solid State Physics by Omar
5. Introduction to Condensed Matter Physics by Duan

Contributors and Attributions

• ContribMSE5317