13.7: Questions

What is the main reason for the predominance of trans states in crystalline polyethylene?

a	Allows better chain packing to produce a denser structure
b	Each trans state is lower in energy due to steric hindrance effects
c	The all-trans conformation is entropically favoured
d	Formation of chain-folded lamellae requires trans states

Answer

B. Whilst statements (a) and (d) are certainly true (and (c) is definitely false) it is the lower energy of the trans states due to steric interactions between constituents that drives crystallisation in most polymers. Chain folding is a kinetic necessity, as the nucleation of chain-extended crystals would be too slow for polymers of high molecular weight. In fact, polymers containing bulky side-groups are generally inhibited from crystallising and instead form glassy structures.

Rank these structural features of a quenched high molecular weight semi-crystalline polymer in order of their size, smallest first (based on average values - there will be some overlap in ranges):

1. Chain length
2. Lamellar thickness
3. Spherulite radius
4. Root-mean-squared end-to-end distance of chains

a	B, D, C, A
b	A, C, B, D
c	D, C, A, B
d	C, B, D, A

Answer

a. Provided the sample is quenched, the lamellar thickness should be smaller than the r.m.s. end-to-end distance. This is because the lamellae are much wider and broader than they are thick, and there is some memory of the random coil configuration in the melt, with each chain participating in several different lamellae. The spherulite radius is typically 1-10 microns, depending on the polymer and crystallisation conditions, whereas the chain length could be much larger than this for a high molecular weight polymer.

PHB (polyhydroxybuturyate) is a naturally occurring, biodegradable polymer produced by bacteria, which melts at around 200°C and forms large spherulites readily on cooling. What sort of heat treatment would result in a solid with mechanical properties most suitable for a making a fizzy drinks bottle?

a	Annealing at 100°C for one hour
b	Heating to just above 200°C until melted, followed by rapid quench to room temperature
c	Heating to just above 200°C until melted, followed by rapid quench to room temperature, and annealing at 100°C for one hour
d	Heating to just 200°C until melted, followed by a slow cooling to room temperature

Answer

C. Annealing at 100°C for one hour would allow some transformation of the polymer to its crystalline form, but since the thermal history of the sample is unknown it is best to melt the solid first. A rapid quench would result in the nucleation of a large number of small spherulites, giving a high amorphous content solid with poor mechanical properties. Slow cooling would improve matters, but the initial spherulite density would be low so the final solid would contain large spherulites and tend to be rather weak and brittle. An initial fast quench, followed by annealing, should produce a highly crystalline solid with small spherulites, which is the best possible microstructure to achieve good strength and stiffness to resist the pressure inside a fizzy drinks bottle.

During a tensile test of a polyethylene dumbbell sample at room temperature using a strain rate of 10 mm/min, at what position relative to the sample is failure most likely to occur? Justify your answer in terms of the changes in polymer chain orientation in the sample during tensile draw.

a	Exactly at the mid-point between the jaws of the tensile tester
b	Exactly in the middle of the neck
c	Equally likely at either end of the dumbbell, where the neck meets the amorphous region
d	At one end of the dumbbell, furthest from the point at which the necking originated

Answer

D. Watch the movie of the tensile test again, slowly. The polymer chains in the neck are highly aligned, and material is drawn out from the amorphous regions at either end of the dumbbell (notice that the polymer in the neck itself does not stretch, but the neck simply extends as more amorphous material is aligned). The end furthest from the origin point of the neck contains the most amorphous material, and therefore will therefore extend until no more material can be draw out, at which point brittle failure occurs at the junction between the neck and the remaining material around the jaws.

How are polymer chains able to form crystallites?

Answer

Polymers are long chain molecules that are folded and twisted along their length. A bulk sample contains an enormous number of chains of varied lengths and with a range of molecular masses. Crystallites occur in regions where there is an ordered arrangement of sections of polymer chains. A single chain can pass through a single crystallite on many occasions and will pass through both amorphous and crystalline regions of a bulk polymer. When a polymer crystallises, lamellae are generally the first structure to be formed, which grow into more complex three-dimensional structures such as spherulites. In a crystallite, chains can be arranged parallel to each other or in other arrangements such as helices in which sections of chains are twisted around each other with a regular repeated sequence. For crystallites to form on cooling, a sample must be cooled slowly enough to allow ordered regions to arrange themselves. In general a quenched polymer will cool too quickly to allow any crystallites to form.

Which distinctive shape is seen when observing a spherulite between crossed polars? Explain why this shape is seen.

Answer

When observing a spherulite between crossed polars, a distinctive Maltese cross pattern is seen. The arms of the cross are parallel to the crossed polarising filters below and above the specimen. This pattern occurs as a consequence of the orientation of crystal lattice axes and the fact that in an anisotropic material, e.g. a polymer crystal, each lattice axis has a different refractive index. That the cross remains stationary relative to the filters if the polymer is rotated on the microscope stage, demonstrates that the optic axes are tangential and radial in the spherulite.

A second feature of spherulites is visible in polarised light. The radiating fibrous appearance occurs due to lamellae within the spherulite having a variety of orientations.

State two techniques that could be used to determine the degree of crystallinity of a polymer.

Answer

Two methods that could be used to determine the degree of crystallinity of a polymer are x-ray diffraction (XRD) and differential scanning calorimetry (DSC).

Describe and explain the form of a stress-strain curve for a semi-crystalline polymer subjected to a uniaxial stress above its glass transition temperature.

Answer

The general form of the stress-strain curve is shown below. Hooke's law is obeyed in the initial elastic region; deformation is uniform and reversible. The dip in the curve occurs after yield and is a consequence of the reduction in local area that occurs when the sample begins to neck. There is then a flat region of the curve, during which the sample is cold drawing as the sample necks along its entire length and the chains align themselves parallel to the direction of the applied force. The final rise in the curve before failure is due to strain hardening.

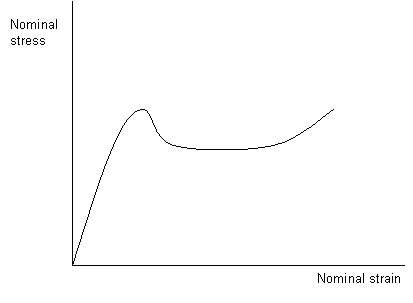
A stress-strain curve for a semi-crystalline polymer subjected to a uniaxial stress above its glass transition temperature

Describe how Considère's construction can explain the phenomenon of necking and stable cold drawing in polymers. What other types of behaviour may be observed for a polymer sample subjected to a uniaxial stress?. What other types of behaviour may be observed for a polymer sample subjected to a uniaxial stress?

Answer

For a sample under uniaxial tension, there is an observed drop in nominal stress at the onset of necking. At this point:

\[\frac{d \sigma}{d \lambda}=0\]

Where σ is the nominal stress and λ is the extension ratio, which is defined as the current length divided by the initial length and is therefore related to the nominal strain; an extension ratio of 1 corresponds to 0% strain. By conservation of volume it can be shown that:

\[\sigma=\frac{\sigma_{t}}{\lambda}\]

Therefore

\[\frac{d \sigma}{d \lambda}=\frac{1}{\lambda} \frac{d \sigma_{t}}{d \lambda}-\frac{\sigma_{t}}{\lambda^{2}}\]

In these expressions σ_t is the true stress, which is equal to the applied force divided by the instantaneous area. Since \(\frac{d \sigma}{d \lambda}=0\) at the onset of necking, it follows that at the onset of necking the condition below is satisfied.

\[\frac{d \sigma_{t}}{d \lambda}=\frac{\sigma_{t}}{\lambda}\]

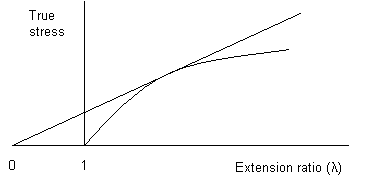
True stress plotted against extension ratio, showing Considère's construction for the onset of necking

From the plot above, of true stress versus extension ratio, it is possible to determine whether necking will occur. A tangent to the curve constructed from λ = 0, touches the curve at the point where necking starts. This is Considère's construction.

As in the plot below, it is sometimes possible to draw a second tangent to the curve from λ = 0, which touches the curve at a higher extension ratio. In the region between the points where the tangents touch the curve, the polymer exhibits stable cold drawing; the point where the second tangent touches the curve corresponds to the limiting strain in the neck. In conclusion three types of behaviour may be recognised:

If \(\frac{d \sigma_{t}}{d \lambda}>\frac{\sigma_{t}}{\lambda}\) at all times, no necking occurs; the material extends uniformly until failure.

If \(\frac{d \sigma_{t}}{d \lambda}=\frac{\sigma_{t}}{\lambda}\) at one point on the curve, then the material will neck and fail.

If \(\frac{d \sigma_{t}}{d \lambda}=\frac{\sigma_{t}}{\lambda}\) at two points, then necking will be followed by cold drawing.

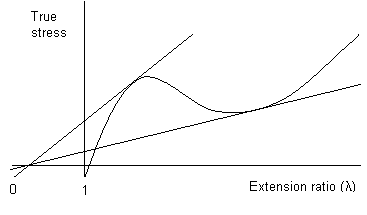
True stress plotted against extension ratio, showing the double tangent construction for stable cold drawing

Compare and contrast features of the crystallisation in polymers with that in other types of materials, such as metals and ceramics.