16.7: Porous Structures in Bending
- Page ID
- 31619
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
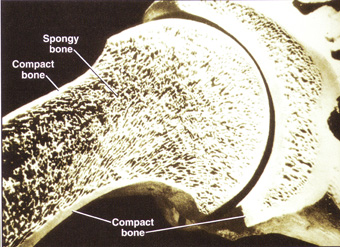
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Porous structures are often used as a lightweight core separating two strong, stiff outer layers to form a sandwich panel. Like the I-beam, such structures have a greater resistance to bending per unit weight of material than a solid beam and so are useful where weight-saving and stiffness are important. Typical applications include flooring panels in aircraft or rotors in helicopter blades. Sandwich structures are also common in biological structures, such as leaves or spongy bone.
 |
 |
|
From J. Banhart, Manufacture, Characterisation and Application of Cellular Metals and Metal Foams, Progress Mater. Sci., 2001, 46, pp.559-632. |
From Cell Biology by Thomas D. Pollard and William C. Earnshaw, Saunders 2004, pp.540 (Figure 34-4), courtesy of D.W. Fawcett, Harvard Medical School. |
However some porous solids, such as wood are used without the stiff, strong outer layers. We might ask whether it is generally true, or under what conditions a porous rod will be stiffer in bending (i.e. give a smaller deflection for a given applied force) than a solid rod of the same length and overall mass.
Consider two rods one is porous and the other is solid. As each rod has the same length and mass and a circular cross-section, the porous one must have a larger radius.
The deflection, δ, of a cantilevered beam of length L under an imposed force W is given by
\[\delta=\frac{1}{3} \frac{W L^{3}}{E I}\]
For given values of W and L an increase in beam stiffness requires a higher value of the product EI. For a beam of circular cross-section <I = πr4/4. The porous beam has a larger radius and therefore a larger moment of area than the solid beam. However the porous beam also has a lower Young modulus. For the porous beam to be stiffer in bending, the rate at which the moment of area increases with radius must therefore be greater than the rate at which the Young modulus decreases.
If the density of the porous beam is ρ and solid beam is ρS and both have the same length and mass, then the ratio of the radius of the porous beam, r, to that of the solid beam, rS, is
\[\left(\frac{\rho_{\mathrm{S}}}{\rho}\right)=\left(\frac{r}{r_{\mathrm{S}}}\right)^{2}\]
As I ∝ r4 the ratio of the second moments of area of the porous and solid beams, I and IS respectively, is
\[\frac{I}{I_{\mathrm{S}}}=\left(\frac{\rho_{\mathrm{S}}}{\rho}\right)^{2}\]
In other words I/IS increases as the inverse square of the relative density, ρ/ρS.
Now the expression derived above for the elastic modulus of an open-cell porous body was
\[\frac{E}{E_{\mathrm{S}}}=k\left(\frac{\rho}{\rho _\mathrm{s}}\right)^{2}\]
That is E/ES decreases as the square of the relative density. In other words although I is increasing with decreasing density, E is decreasing at the same rate. In this case there would be no advantage in using such a material in bending compared with the solid material.
As nothing can be done about the change in radius, and hence I, with relative density, a higher bending stiffness can only be obtained by ensuring that E/ES varies with ρ/ρS by a power less than 2. This is the case for the axial Young modulus of wood where the exponent lies closer to 1 rather than 2, as shown below.
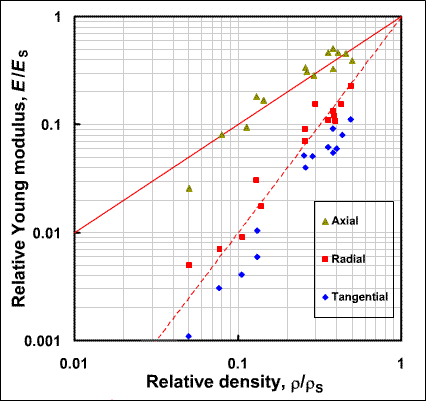
(The data is taken from K.E. Easterling et al, “On the mechanics of balsa and other woods”, Proc. Roy. Soc. A, 383[1784] (1982) 31-41.) Such changes can be brought about by varying the cell structure, for instance by elongating the cells, as occurs in wood. However in the transverse (radial and tangential) directions E/ES for wood decreases much more rapidly with decreasing ρ/ρS. Here the exponent lies between 2 and 3.


